動態

詳情 返回 返回

如果你的PyTorch優化器效果欠佳,試試這4種深度學習中的高級優化技術吧 - 動態 詳情

在深度學習領域，優化器的選擇對模型性能至關重要。雖然PyTorch中的標準優化器如

SGD

、

Adam

和

AdamW

被廣泛應用，但它們並非在所有情況下都是最優選擇。本文將介紹四種高級優化技術，這些技術在某些任務中可能優於傳統方法，特別是在面對複雜優化問題時。

我們將探討以下算法：

  1. 序列最小二乘規劃（SLSQP）
  2. 粒子羣優化（PSO）
  3. 協方差矩陣自適應進化策略（CMA-ES）
  4. 模擬退火（SA）

這些方法的主要優勢包括：

  1. 無梯度優化：適用於非可微操作，如採樣、取整和組合優化。
  2. 僅需前向傳播：通常比傳統方法更快，且內存效率更高。
  3. 全局優化能力：有助於避免局部最優解。

需要注意的是，這些方法最適合優化參數數量較少（通常少於100-1000個）的情況。它們特別適用於優化關鍵參數、每層特定參數或超參數。

實驗準備

在開始實驗之前，我們需要設置環境並定義一些輔助函數。以下是必要的導入和函數定義：

 fromfunctoolsimportpartial
 fromcollectionsimportdefaultdict
 importtorch
 importtorch.nnasnn
 importtorch.optimasoptim
 importtorch.nn.functionalasF
 importnumpyasnp
 importscipy.optimizeasopt
 importmatplotlib.pyplotasplt
 
 # 設置隨機種子以確保結果可復現
 torch.manual_seed(42) 
 np.random.seed(42)  
 
 # 輔助函數：在PyTorch模型和NumPy向量之間轉換權重
 defset_model_weights_from_vector(model, numpy_vector):
     weight_vector=torch.tensor(numpy_vector, dtype=torch.float64)
     model[0].weight.data=weight_vector[0:4].reshape(2, 2)
     model[2].weight.data=weight_vector[4:8].reshape(2, 2)
     model[2].bias.data=weight_vector[8:10]
     returnmodel
 
 defget_vector_from_model_weights(model):
     returntorch.cat([
         model[0].weight.data.view(-1), 
         model[2].weight.data.view(-1), 
         model[2].bias.data]
     ).detach().numpy()
 
 # 用於跟蹤和更新損失的函數
 defupdate_tracker(loss_tracker, optimizer_name, loss_val):
     loss_tracker[optimizer_name].append(loss_val)
     iflen(loss_tracker[optimizer_name]) >1:
         min_loss=min(loss_tracker[optimizer_name][-2], loss_val)
         loss_tracker[optimizer_name][-1] =min_loss
     returnloss_tracker

這些函數將用於在不同的優化算法之間轉換模型權重，並跟蹤優化過程中的損失。

接下來定義目標函數和PyTorch優化循環：

 defobjective(x, model, input, target, loss_tracker, optimizer_name):
     model=set_model_weights_from_vector(model, x)
     loss_val=F.mse_loss(model(input), target).item()
     loss_tracker=update_tracker(loss_tracker, optimizer_name, loss_val)  
     returnloss_val
 
 defpytorch_optimize(x, model, input, target, maxiter, loss_tracker, optimizer_name="Adam"):
     set_model_weights_from_vector(model, x)
     optimizer=optim.Adam(model.parameters(), lr=1.) 
 
     # 訓練循環
     foriterationinrange(maxiter):  
         loss=F.mse_loss(model(input), target)
         optimizer.zero_grad()  
         loss.backward()        
         optimizer.step()
         loss_tracker=update_tracker(loss_tracker, optimizer_name, loss.item())  
     final_x=get_vector_from_model_weights(model)
     returnfinal_x, loss.item()

最後設置實驗所需的通用變量：

 model=nn.Sequential(nn.Linear(2, 2, bias=False), nn.ReLU(), nn.Linear(2, 2, bias=True)).double()
 input_tensor=torch.randn(32, 2).double()  # 隨機輸入張量
 input_tensor[:, 1] *=1e3  # 增加一個變量的敏感度
 target=input_tensor.clone() # 目標是輸入本身（恆等函數）
 num_params=10
 maxiter=100
 x0=0.1*np.random.randn(num_params)
 loss_tracker=defaultdict(list)

這些設置為我們的實驗創建了一個簡單的神經網絡模型、定義了輸入、目標和初始參數。

在下一部分中，我們將開始實現和比較不同的優化技術。

優化技術比較

1、PyTorch中的Adam優化器

作為基準，我們首先使用PyTorch的Adam優化器。Adam是一種自適應學習率優化算法，在深度學習中廣泛使用。

 optimizer_name="PyTorch Adam"
 result=pytorch_optimize(x0, model, input_tensor, target, maxiter, loss_tracker, optimizer_name)
 print(f'Adam優化器最終損失: {result[1]}')

運行此代碼後，我們得到以下結果：

 Adam優化器最終損失: 91.85612831226527

考慮到初始損失值約為300,000，這個結果在100次優化步驟後已經有了顯著改善。

2、序列最小二乘規劃 (SLSQP)

序列最小二乘規劃（SLSQP）是一種強大的優化算法，特別適用於具有連續參數的問題。它通過在每一步構建二次近似來逼近最優解。

 optimizer_name="slsqp"
 args= (model, input_tensor, target, loss_tracker, optimizer_name)
 result=opt.minimize(objective, x0, method=optimizer_name, args=args, options={"maxiter": maxiter, "disp": False, "eps": 0.001})
 print(f"SLSQP優化器最終損失: {result.fun}")

運行SLSQP算法，我們獲得以下結果：

 SLSQP優化器最終損失: 3.097042282788268

SLSQP的性能明顯優於Adam，這表明在某些情況下，非傳統優化方法可能更有效。

3、粒子羣優化 (PSO)

粒子羣優化（PSO）是一種基於羣體智能的優化算法，其靈感來自於鳥羣和魚羣的社會行為。PSO在非連續和非光滑的問題上表現尤為出色。

 frompyswarmimportpso
 
 lb=-np.ones(num_params)
 ub=np.ones(num_params)
 optimizer_name='pso'
 args= (model, input_tensor, target, loss_tracker, optimizer_name)
 result_pso=pso(objective, lb, ub, maxiter=maxiter, args=args)
 print(f"PSO優化器最終損失: {result_pso[1]}")

PSO的優化結果如下：

 PSO優化器最終損失: 1.0195048385714032

PSO的表現進一步超越了SLSQP，這凸顯了在複雜優化問題中探索多種算法的重要性。

4、協方差矩陣自適應進化策略 (CMA-ES)

協方差矩陣自適應進化策略（CMA-ES）是一種高度複雜的優化算法，特別適用於難以處理的非凸優化問題。它通過自適應地學習問題的協方差結構來指導搜索過程。

 fromcmaimportCMAEvolutionStrategy
 
 es=CMAEvolutionStrategy(x0, 0.5, {"maxiter": maxiter, "seed": 42})
 optimizer_name='cma'
 args= (model, input_tensor, target, loss_tracker, optimizer_name)
 whilenotes.stop():
     solutions=es.ask()
     object_vals= [objective(x, *args) forxinsolutions]
     es.tell(solutions, object_vals)
 print(f"CMA-ES優化器最終損失: {es.result[1]}")

CMA-ES的優化結果如下：

 (5_w,10)-aCMA-ES (mu_w=3.2,w_1=45%) in dimension 10 (seed=42, Thu Oct 12 22:03:53 2024)  
 CMA-ES優化器最終損失: 4.084718909553896

雖然CMA-ES在這個特定問題上沒有達到最佳性能，但它在處理複雜的多模態優化問題時通常表現出色。

5、 模擬退火 (SA)

模擬退火（SA）是一種受冶金學啓發的優化算法，它模擬了金屬冷卻和退火過程。SA在尋找全局最優解方面特別有效，能夠避免陷入局部最優解。

 fromscipy.optimizeimportdual_annealing
 bounds= [(-1, 1)] *num_params
 optimizer_name='simulated_annealing'
 args= (model, input_tensor, target, loss_tracker, optimizer_name)
 result=dual_annealing(objective, bounds, maxiter=maxiter, args=args, initial_temp=1.)
 print(f"SA優化器最終損失: {result.fun}")

SA的優化結果如下：

 SA優化器最終損失: 0.7834294257939689

可以看到，針對我們的問題SA表現最佳，這突顯了其在複雜優化問題中的潛力。

下面我們來可視化這些優化器的性能，並討論結果的含義。

結果可視化與分析

為了更好地理解各種優化算法的性能，我們將使用matplotlib庫來可視化優化過程中的損失變化。

 plt.figure(figsize=(10, 6))
 line_styles= ['-', '--', '-.', ':']
 fori, (optimizer_name, losses) inenumerate(loss_tracker.items()):
     plt.plot(np.linspace(0, maxiter, len(losses)), losses, 
              label=optimizer_name, 
              linestyle=line_styles[i%len(line_styles)], 
              linewidth=5,
     )
 plt.xlabel("Iteration", fontsize=20)
 plt.ylabel("Loss", fontsize=20)
 plt.ylim(1e-1, 1e7)
 plt.yscale('log')
 plt.title("Loss For Different Optimizers", fontsize=20)
 plt.grid(True, linestyle='--', alpha=0.6)
 plt.legend(loc='upper right', fontsize=20)
 plt.tight_layout()
 plt.savefig('optimizers.png')
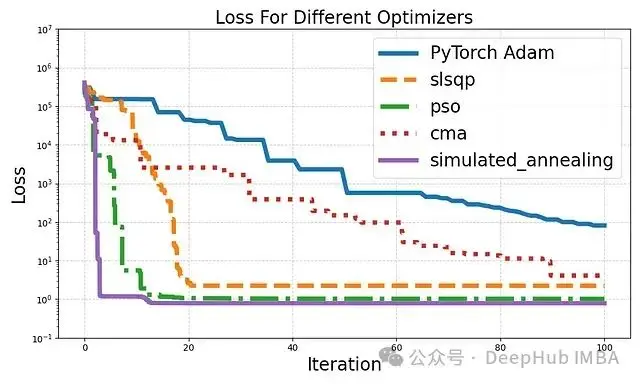
 plt.show()

執行上述代碼後，我們得到了以下可視化結果：

結果分析

  1. Adam優化器：作為基準Adam表現穩定但收斂速度相對較慢。這反映了在某些複雜問題中，傳統梯度下降方法可能不是最優選擇。
  2. SLSQP：序列最小二乘規劃表現出快速的初始收斂，這表明它在處理具有連續參數的問題時非常有效。
  3. PSO：粒子羣優化展示了良好的全局搜索能力，能夠迅速找到較好的解。這凸顯了其在非凸優化問題中的潛力。
  4. CMA-ES：雖然在本實驗中收斂較慢，但協方差矩陣自適應進化策略通常在處理高度複雜和多模態的問題時表現出色。其性能可能在更復雜的優化場景中更為突出。
  5. 模擬退火：我們這個特定問題SA表現最為出色，僅用幾次迭代就達到了最低損失。這突顯了其在避免局部最優解並快速找到全局最優解方面的優勢。

需要注意的是，每種算法的"迭代"定義可能不同，因此直接比較迭代次數可能不夠公平。例如SA的每次迭代可能包含多次目標函數評估。

總結

在特定問題上，非傳統優化方法可能比標準的梯度下降算法（如Adam）表現更好。然而，這並不意味着這些方法在所有情況下都優於傳統方法。選擇最適合的優化算法應基於具體問題的特性：

  1. 對於參數數量較少（100-1000個）的優化問題，考慮嘗試本文介紹的高級優化技術。
  2. 在處理非可微操作或複雜的損失景觀時，無梯度方法（如PSO、CMA-ES和SA）可能更有優勢。
  3. 對於需要滿足複雜約束的優化問題，SLSQP可能是一個很好的選擇。
  4. 在計算資源有限的情況下，考慮使用僅需前向傳播的方法，如PSO或SA。
  5. 對於高度非凸的問題，CMA-ES和SA可能更容易找到全局最優解。

最後，建議在實際應用中對多種優化方法進行比較和測試，以找到最適合特定問題的算法。同時要注意這些高級方法在大規模問題（參數數量超過1000）上可能面臨計算效率的挑戰。

未來研究方向

  1. 探索這些高級優化技術在更復雜的深度學習模型中的應用。
  2. 研究如何有效地將這些方法與傳統的梯度下降算法結合，以開發混合優化策略。
  3. 開發更高效的並行化實現，以提高這些算法在大規模問題上的適用性。
  4. 探索這些方法在特定領域（如強化學習、神經架構搜索）中的潛在應用。

通過深入理解和靈活運用這些高級優化技術，研究者和工程師可以在面對複雜優化問題時拓展解決方案的範圍，potentially unlocking新的性能水平和應用可能性。

參考文獻

  1. Hansen, N. (2016). The CMA Evolution Strategy: A Tutorial. arXiv preprint arXiv:1604.00772.
  2. Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN'95 - International Conference on Neural Networks, 4, 1942-1948.
  3. Nocedal, J., & Wright, S. J. (1999). Numerical Optimization. New York: Springer.
  4. Tsallis, C., & Stariolo, D. A. (1996). Generalized simulated annealing. Physica A: Statistical Mechanics and its Applications, 233(1-2), 395-406.
  5. Kingma, D. P., & Ba, J. (2014). Adam: A Method for Stochastic Optimization. arXiv preprint arXiv:1412.6980.
  6. Ruder, S. (2016). An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747.

https://avoid.overfit.cn/post/d9fedfc22d594ba0a2b7e6a896adcf6c

pytorch , 人工智能 , 神經網絡 , 優化 , 深度學習
user avatar chaoqiezi 頭像 yekai_620f63e12c172 頭像
點贊 2 用戶, 點贊了這篇動態!
點贊

Add a new 評論

Some HTML is okay.