Optuna在8月18日發佈了最近的 v4.5版，加入了GPSampler的約束多目標優化功能，我們來看看這個新的功能。

基於高斯過程的貝葉斯優化（GPBO）最近幾年在材料科學、機器學習等領域應用很廣。GPSampler最初設計時就想做一個簡單好用的GPBO實現。雖然在定製方面（比如核函數、獲取函數）沒有BoTorch和Ax那麼靈活，但GPSampler勝在速度快，依賴少。

早期版本的GPSampler支持的問題類型比較有限，但是經過團隊持續改進。v4.2版本加入了不等式約束支持，v4.4版本實現了多目標優化。現在v4.5直接支持約束多目標優化了。

這個功能在很多實際場景中都很有用，比如説：材料科學、機器學習、藥物發現這些領域經常需要在物理約束或實驗限制下平衡多個目標。Optuna v4.5的約束多目標GPBO直接解決了這個需求，可能會推動相關領域的研究進展。

安裝和基本使用

GPSampler需要額外安裝幾個依賴包：

 $ pip install optuna==4.5.0  
   
 # scipy和torch對於GPSampler也是必需的。  
 $ pip install scipy  
 $ pip install torch --index-url https://download.pytorch.org/whl/cpu

安裝完成後，使用起來很直接：

 import optuna
def objective(trial: optuna.Trial) -> tuple[float, float]:
    x = trial.suggest_float("x", -5.0, 5.0)
    y = trial.suggest_float("y", -5.0, 5.0)
    c = x**2 + y**2 - 4.0
    trial.set_user_attr("c", c)
    return x**2 + y**2, (x - 2) ** 2 + (y - 2) ** 2

def constraints(trial: optuna.trial.FrozenTrial) -> tuple[float]:
    c = trial.user_attrs["c"]
    return (c,)
sampler = optuna.samplers.GPSampler(constraints_func=constraints)
study = optuna.create_study(sampler=sampler, directions=["minimize"] * 2)
 study.optimize(objective, n_trials=100)

多目標優化的技術實現

GPSampler的多目標優化採用了Expected Hypervolume Improvement (log EHVI)的對數形式作為獲取函數。這個實現主要基於Daulton等人[1]的方程(1)和Lacour等人[6]的算法2。

幾個關鍵的技術改進都體現在相關的PR中：

PR #6039實現了盒分解算法，大幅提升了超體積改進計算的速度。PR #6052引入了基於準蒙特卡羅的log EHVI實現。PR #6069則在GPSampler中正式加入了多目標優化功能。

盒分解算法帶來的性能提升相當明顯。相比原生的實現，速度提升了6到800倍，讓四目標問題的優化變得可行。雖然整體思路和BoTorch的實現接近，但具體實現細節有些不同。

在多目標優化基礎上，GPSampler現在可以處理不等式約束了。這部分參考了J. Gardner等人[3]和M. Gelbart等人[4]的方法。

系統同時為目標函數和約束函數建立GP模型，不過暫時忽略了它們之間的相關性。PR #6198實現了約束log EHVI，PR #6224則完成了約束多目標優化的完整支持。

約束處理的核心是用Probability of Improvement (PI)來評估候選點的可行性。最終的獲取函數就是EHVI和可行性概率的乘積。

性能測試對比

為了驗證約束多目標優化的效果，團隊做了詳細的基準測試。主要對比了幾種情況：

一是和不考慮約束的多目標GPSampler比較，看約束處理帶來的好處。二是和Optuna中已有的TPESampler、NSGAIISampler對比，這兩個也支持約束多目標優化。

測試環境設置

測試問題選擇了C2-DTLZ2，這是OptunaHub新加的約束多目標優化基準問題。設置為2個目標，3個變量。

每次優化跑300輪試驗，用5個不同隨機種子重複測試來計算標準誤差。由於C2-DTLZ2是確定性問題（目標函數沒有噪聲），GPSampler開啓了

deterministic_objective=True

選項。

測試機器配置：Arch Linux系統，Intel Core i9-14900HX處理器（24核32線程，最高5.8GHz），Python 3.11.0。

帕累託前沿質量對比

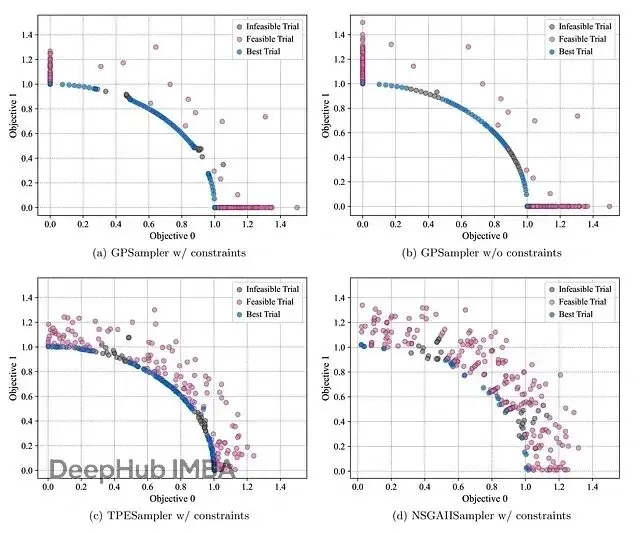
圖1展示了不同算法獲得的帕累託前沿分佈。

圖1. 300次試驗後C2-DTLZ2問題的獲得帕累託前沿。結果顯示約束GPSampler（如(a)所示）與無約束GPSampler（如(b)所示）和TPESampler（如(c)所示）相比，有效地減少了不可行區域中的浪費評估（灰色着色），而NSGAIISampler（如(d)所示）在300次試驗後仍遠未收斂。

約束處理的效果很明顯

C2-DTLZ2問題故意在帕累託前沿上設置了不可行區域，專門測試算法處理斷開帕累託前沿的能力[5]。雖然不考慮約束也能找到一些帕累託解，但會在不可行區域浪費很多評估次數。

對比約束版GPSampler（圖1a）和無約束版本（圖1b），約束版本在可行帕累託解（藍色點）之間產生的不可行觀察（灰色點）明顯更少。説明約束處理確實起作用了，減少了無效評估。

和其他採樣器的比較

相比TPESampler（圖1c），GPSampler（圖1a）在不可行區域的浪費評估也更少。不過TPESampler在某個目標值接近零的帕累託前沿區域覆蓋得更全面一些。

這主要是GP獲取函數的特性導致的——傾向於在邊界附近過度採樣，降低了那些區域的不確定性，但也讓進一步探索相鄰帕累託前沿變得困難。

NSGAIISampler的表現就比較一般了（圖1d），300次試驗後還沒收斂，找到的最優解很少。

收斂速度分析

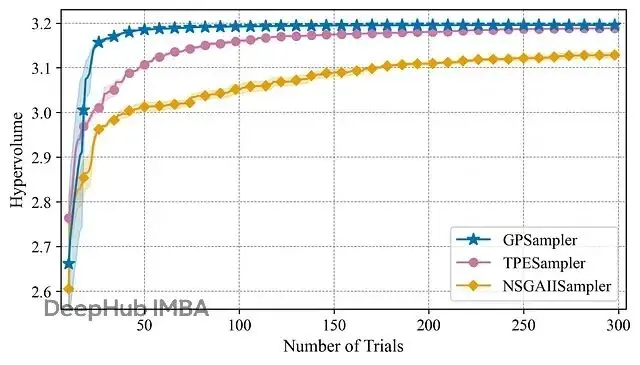
圖2的可行超體積歷史更直觀地展示了各算法的收斂表現。

圖2. C2-DTLZ2問題[5]的可行超體積歷史。實線表示均值，陰影區域表示標準誤差，兩者都是在具有不同隨機種子的五次獨立運行中計算的。約束GPSampler（藍色）與TPESampler（粉色）和NSGAIISampler（黃色）相比，實現了更快的收斂到更高的超體積值，證明了新功能在減少評估成本方面的有效性。

GPSampler的超體積增長曲線很有意思。不到50次試驗就達到了TPESampler的最終水平，比NSGAIISampler領先得更多。這種快速收斂對計算成本高的優化問題特別重要——減少函數評估次數就是直接節省時間。

總結

Optuna v4.5的GPSampler約束多目標優化功能確實是個不錯的更新。C2-DTLZ2基準測試證明了幾點：減少了不可行區域的無效評估，可行超體積收斂比TPESampler和NSGAIISampler都快。

這讓Optuna在處理計算昂貴的黑盒優化問題時更有競爭力了。如果你的項目涉及約束多目標優化，值得試試這個新功能。

參考文獻

[1] Daulton, S., Balandat, M., and Bakshy, E. Differentiable expected hypervolume improvement for parallel multi-objective Bayesian optimization. In Advances in Neural Information Processing Systems, volume 33, pp. 9851–9864, 2020.

[2] Deb, K., Thiele, L., Laumanns, M., and Zitzler, E. Scalable test problems for evolutionary multi-objective optimization. In Evolutionary Multi-objective Optimization, pp. 105–145. Springer-Verlag, 2005.

[3] Gardner, J., Kusner, M., Zhixiang, W., Weinberger, K., and Cunningham, J. Bayesian Optimization with Inequality Constraints. In Proceedings of the 31st International Conference on Machine Learning, volume 32, pp. 937–945. PMLR, 2014.

[4] Gelbart, M. A., Snoek, J., and Adams, R. P. In Proceedings of the 30th Conference on Uncertainty in Artificial Intelligence, pp. 250–259. AUAI Press, 2014.

[5] Jain, H., and Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. In IEEE Transactions on Evolutionary Computation, 18(4):602–622, 2014.

[6] Lacour, R., Klamroth, K., and Fonseca, CM. A box decomposition algorithm to compute the hypervolume indicator. Computers & Operations Research, volume 79, pp. 347–360, 2017.

https://avoid.overfit.cn/post/2223f043ade548cc8a33494b8eae6331

作者：Kaito Baba