在數據科學的實際工作中，我們經常會遇到這樣的情況：手頭的真實數據要麼不夠用，要麼因為隱私合規問題無法直接使用，但這些數據往往包含重要的統計規律，但直接拿來做實驗或測試卻十分的麻煩。

這時候合成數據就派上用場了，簡單説就是根據現有數據集的分佈特徵，人工創造出任意數量的新數據行，讓這些"假數據"在統計意義上跟真實數據無法區分。聽起來像是是在"造假"，但實際上這是一項真正的技術活——既要保證數據的真實性（統計規律相符），又要確保隱私性（無法反推個體）。

合成數據的應用場景非常廣泛：異常檢測模型需要大量邊緣案例來訓練，但真實異常樣本稀缺；敏感數據需要脱敏處理，生成統計特徵相似但無法追溯的數據；軟件系統測試需要海量數據，但真實數據獲取成本高昂。不管做哪個方向的數據科學工作，掌握幾種合成數據生成方法都是最近本的要求。

本文將重點介紹如何讓合成數據在分佈特徵和列間關係上都跟真實數據保持一致。我們會介紹兩種基於多項式分佈的實踐方法，不預設具體應用場景，純粹從技術角度拆解生成過程。

最簡單的生成方式

最直接的思路就是逐行逐單元格地生成數據，每個單元格獨立生成，互不影響。這個辦法確實簡單粗暴，在某些場景就夠用，並且也是其他複雜方法的基礎。

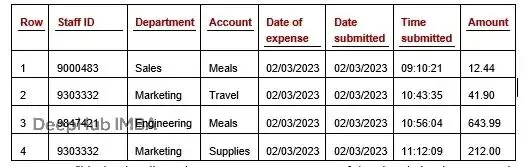
假設有這麼一張真實數據表：

這是某公司某段時間的員工報銷記錄，七個字段（實際業務數據字段會更多）。

現在有10,000行真實數據，想再生成10,000行類似的。首先得摸清每列的分佈規律。

員工ID這列有一堆固定值，每個值在總記錄裏佔一定比例。比如員工ID 9000483可能佔1.2%，93003332佔0.8%，以此類推。部門、賬户、費用日期、提交日期這幾列也類似。提交時間可以當數值處理（從午夜零點開始的秒數）。金額就是純數值了。

數值列的分佈有好幾種建模方式。一種是假定它符合某個理論分佈，擬合參數就行。高斯分佈用均值和標準差，泊松分佈用lambda參數。對於金額這種數據，對數正態分佈應該會更貼近現實。

或者直接用distfit這類工具也行，讓它自動試一遍各種分佈，挑最合適的，再擬合參數。

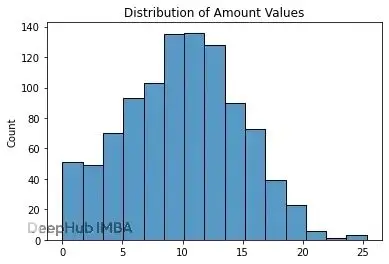
這裏採用直方圖建模，簡單又靈活，多峯分佈這種複雜情況也能搞定。假設金額列用15個bin分箱後長這樣：

那麼建模步驟就是：

分類列：枚舉所有唯一值，統計各自出現頻率； 數值列：用直方圖表示分佈。

然後開始逐行生成。每行先選員工ID，按真實數據裏的頻率隨機抽。高頻ID在合成數據裏出現頻率也高，低頻ID還是低頻。

也可以允許生成全新的值，比如真實數據裏沒見過的員工ID、部門、賬户等等。我們這裏為了簡單暫時不考慮這種情況，但實際應用中應該挺常見的（生成合理的新需要花更多的功夫）。

其他列同理。分類列繼續按頻率抽，數值列先按概率選一個bin，再在bin範圍內隨機取值。

拿上面那個直方圖來説，先在15個bin裏選一個。第6、7個bin被選中的概率最大（因為它們計數高），第14個最不可能，但理論上15個都有機會。

每個bin對應一段數值區間，這裏每個bin跨度大概$1.30。可以在區間內均勻採樣，代碼裏用的是另一種辦法：取bin中心值，加點隨機抖動。

下面代碼演示了整個流程。數據集用的是OpenML的棒球數據，每行代表一個球員，16個字段涵蓋賽季數、打數(at bats)、二壘打、三壘打、本壘打、擊球率、打點(RBIs)之類的統計數據。

 import pandas as pd  
import numpy as np  
from sklearn.datasets import fetch_openml  

# Collect the data  
data = fetch_openml('baseball', version=1, parser='auto')   
df = pd.DataFrame(data.data, columns=data.feature_names)  

# Fill any null values, which are only in this one column  
df['Strikeouts'] = df['Strikeouts'].fillna(df['Strikeouts'].median())  

# Divide the features into categorical and numberic, assuming anything with  
# 10 or fewer unique values can be considered categorical  
cat_features = [x for x in df.columns if df[x].nunique() <= 10]   
num_features = [x for x in df.columns if x not in cat_features]  

# Generate the numeric features  
synth_data = []  
for num_feat in num_features:   
  # Create a histogram to represent the distribution of values in   
  # the real data  
  hist = np.histogram(df[num_feat], density=True)   
  bin_centers = [(x+y)/2 for x, y in zip(hist[1][:-1], hist[1][1:])]  
  p = [x/sum(hist[0]) for x in hist[0]]  
  vals = np.random.choice(bin_centers, p=p, size=len(df)).astype(int)  
  vals = [x + (((1.0 * np.random.random()) - 0.5) * df[num_feat].std())  
          for x in vals]  

# Generate the categorical features  
synth_data.append(vals)  
for cat_feat in cat_features:   
  vc = df[cat_feat].value_counts(normalize=True)  
  # Select a random set of value, proportional to the frequency of   
  # each value in this column in the real data  
  vals = np.random.choice(list(vc.index), p=list(vc.values), size=len(df))   
  synth_data.append(vals)  
        
# Convert the array of synthetic data to a pandas dataframe.  
synth_df = pd.DataFrame(synth_data).T  
 synth_df.columns = num_features + cat_features

這樣生成的數據，單個值確實都挺合理。代碼裏做了一個限制：分類字段只從真實數據裏見過的值裏選；數值字段限定在真實數據的最小最大值之間（隨機抖動可能讓個別值稍微越界）。

但跑完之後，數據往往會出現各種離譜的組合。拿員工費用表和棒球數據集來説，可能會生成這樣一行：

員工ID：900043部門：營銷部賬户：重型設備費用日期：2025年1月10日提交日期：2025年1月5日提交時間：晚上11:09金額：$14.44

單看每個字段都沒毛病，但整行一看就不對勁。這員工被調到營銷部了，可同期其他記錄明明顯示他在銷售部。

重型設備這個列偶爾會出現，但營銷部不可能有，更不可能只花$14。提交日期早於費用日期本身就很怪。晚上11點提交這種費用也説不通。

棒球數據集也一樣，特徵多了更難看出來，但問題確實存在。比如可能出現二壘打特別多但三壘打極少的球員，而真實數據裏這倆明顯相關。或者打了很多賽季、本壘打也很多，但打數(at bats)反而很低，這完全不符合常理。

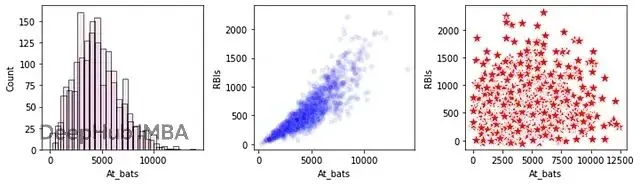
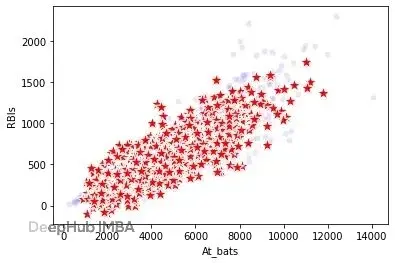
下面這張圖能看得更清楚。三個子圖，第一個展示At_bats的單列分佈，真實數據（藍色）和合成數據（紅色）基本一致。其他字段也差不多。但看第二、三個子圖的兩列聯合分佈就露餡了。中間那個是真實數據裏At_bats和RBIs（打點）的關係，相關性很明顯。右邊是合成數據，相關性直接沒了，出現了一堆離譜的組合。三個及以上字段的關係就更有問題了。

真實數據（藍色）vs 合成數據（紅色）

測試異常檢測系統的話，這種數據倒是挺有用。但如果要生成真實數據，這種方法就走不通了。

合成數據的真正目標

目標其實不只是"真實"，還得"多樣"。如果生成的每一行都完全合理，但所有行都長得差不多，那也沒意義。生成對抗網絡（GANs）碰到"模式崩潰"(mode collapse)時就會這樣，不斷生成幾乎一樣的輸出。

另一個極端是生成的數據雖然真實，但跟某幾行真實數據過於相似。不能單純記憶數據，也不能限制得太死。好的合成數據需要在這之間找平衡——既真實又涵蓋足夠廣的可能性。換句話説，要從"所有合理記錄"的空間裏均勻採樣，更準確説，是從"真實數據裏還沒見過的合理記錄"裏採樣。

從左到右逐列生成

前面那種方法最大的問題在於，單純按頻率獨立生成每個值，導致值的組合完全不靠譜，有時候甚至荒唐。這個根源在於大多數表格數據的字段之間都有關聯，完全獨立的情況很少見。

員工費用表裏，每個員工基本固定在一個或少數幾個部門。每個部門有特定的費用類型和金額範圍。費用發生和提交之間有時間差，等等。

棒球數據也一樣，打的賽季多，打數通常就多；打數多，打點自然也多，安打、本壘打都跟着上去。二壘打和三壘打有相關性。這種關係在數據裏到處都是。

要生成真實數據，必須捕捉這些關聯關係。

一個辦法是逐單元格生成，但每次生成時考慮當前行已經確定的其他值。也就是説，不獨立生成，而是根據已有值來選擇合理的新值。

生成順序可以任意安排。不同順序效果有差異，混合使用不同順序能增加多樣性，我們的演示用從左到右的方法。

拿員工費用表來説，先隨機選員工ID（按真實數據分佈）。然後選部門，這次是隨機但要考慮已選的員工ID，按真實數據裏該員工ID對應的部門分佈來選。接着選賬户，得是在已選員工ID和部門組合下比較合理的。依次類推。最後填金額，根據前面所有列的值選一個合理的數字。這樣一來生成的數據就會非常貼近現實。

下面代碼用隨機森林(Random Forest)來預測每個字段的值，基於已生成的字段。為了效率，一次性生成某個字段的所有行的值，所以是從左往右遍歷字段，每次迭代生成整列數據（根據需要的合成行數）。

開頭跟之前一樣，加載數據，區分數值列和分類列。還是用棒球數據集：

 import pandas as pd  
import numpy as np  
from sklearn.datasets import fetch_openml  

data = fetch_openml('baseball', version=1, parser='auto')  
df = pd.DataFrame(data.data, columns=data.feature_names)  
df['Strikeouts'] = df['Strikeouts'].fillna(df['Strikeouts'].median())  
cat_features = [x for x in df.columns if df[x].nunique() <=10]  
 num_features = [x for x in df.columns if x not in cat_features]

然後修改生成邏輯，改成從左到右：

 from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier  
import matplotlib.pyplot as plt  
import seaborn as sns  

synth_data = []  

# Sets the left-most column based on its distribution only  
feature_0 = df.columns[0]   

# Create a histgram of the first feature  
hist = np.histogram(df[feature_0], density=True)  
bin_centers = [(x+y)/2 for x, y in zip(hist[1][:-1], hist[1][1:])]  
p = [x/sum(hist[0]) for x in hist[0]]  

# Generate as many synthetic rows as there are real rows. We start  
# by creating the full set of synthetic values for the first column.  
vals = np.random.choice(bin_centers, p=p, size=len(df)).astype(int)  
vals = [x + (((1.0 * np.random.random()) - 0.5) * df[feature_0].std())  
        for x in vals]  
synth_data.append(vals)  
synth_cols = [feature_0]  

# Loops through the features after the left-most  
for col_name in df.columns[1:]:   
  print(col_name)  
  synth_df = pd.DataFrame(synth_data).T  
  synth_df.columns = synth_cols  

  if col_name in num_features:  
    # Train a Random Forest on the real data  
    regr = RandomForestRegressor()  
    regr.fit(df[synth_cols], df[col_name])   

    # Predict based on the other synthetic data created so far  
    pred = regr.predict(synth_df[synth_cols])   

    # Adds jitter so that there are not only a small number of unique values  
    vals = [x + (((1.0 * np.random.random()) - 0.5) * pred.std())  
            for x in pred]   
  synth_data.append(vals)  
    
  # If the next column is categorical, populate it in a similar way as with  
  # numeric data.  
  if col_name in cat_features:  
    clf = RandomForestClassifier()  
    clf.fit(df[synth_cols], df[col_name])  
    synth_data.append(clf.predict(synth_df[synth_cols]))  

  # Keep track of the columns we have generated so far  
  synth_cols.append(col_name)  

# Convert the array of data into a pandas dataframe      
synth_df = pd.DataFrame(synth_data).T  
synth_df.columns = synth_cols  

# Display the distribution of At_bats and RBIS, both for the original  
# and the synthetic data  
sns.scatterplot(data=df, x="At_bats", y="RBIs", color='blue', alpha=0.1)  
sns.scatterplot(data=synth_df, x="At_bats", y="RBIs",   
                color='red', marker="*", s=200)  
 plt.show()

跟之前一樣第一列還是隻看分佈生成，但之後每列都基於前面已生成的列來預測。這裏用隨機森林做預測，因為模型能力強，通常能很好地捕捉數據模式。換其他模型或調整隨機森林參數能調節數據的真實度，也能增加多樣性。

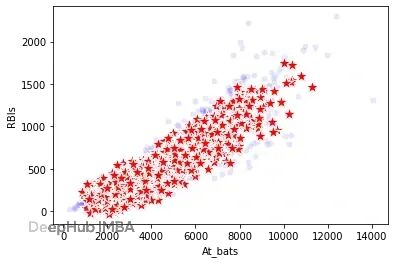
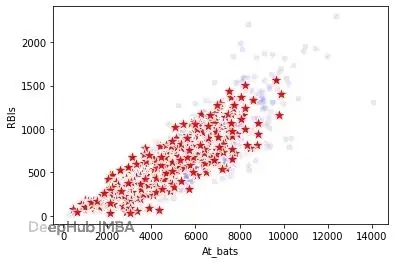
下圖顯示At_bats和RBIs的聯合分佈保持得很好。任意字段組合都差不太多，哪怕是高維組合。

真實數據（藍色圓點）和合成數據（紅色星星）的At_bats與RBIs分佈

這段代碼提供了基本思路，但實際生產環境還得補充幾點。首先，它假設第一列是數值型，棒球數據集確實如此；但第一列也可能是分類型，那就得加類似第一段代碼裏的處理（按頻率隨機選分類值）。也就是：

 vals = np.random.choice(list(vc.index), p=list(vc.values), size=len(df))

如果第一列是分類型就執行這個。變量vc通過調用value_counts()獲得該列每個唯一值的計數。

其次，代碼之所以能跑通，是因為棒球數據集只有一個分類列Position，而且它在最右邊，可以直接從前面生成的數值列預測。

如果有多個分類列，或者分類列右邊還有其他列，代碼就得稍微改一下，雖然改動不大。得能把已生成的分類列作為特徵來預測後續列。如果用Random Forest Classifier（scikit-learn的實現要求X列全是數值），就需要編碼那些分類值，比如獨熱編碼(one-hot encoding)或目標編碼(target encoding)。用predict_proba()比predict()更好，因為它能給出概率分佈。

比如説，假設有兩個分類字段：Position（現在有的）和Team。假設棒球數據集涵蓋20支球隊，所以Team有20個可能值。再假設Team列在最右邊，Position右側。這樣的話，生成Team列時（如果從左到右），就得基於所有其他列（包括編碼後的Position）的合成值。

具體操作是，創建一個Random Forest Classifier用所有其他列預測Team。對Position做獨熱編碼後，除了Team（目標列）之外所有特徵都是數值型，可以餵給Random Forest Classifier。然後在真實數據上訓練，用目前生成的合成數據預測。

用這個Random Forest Classifier時，調用predict_proba()而不是Predict()。這會給每行返回一組20個概率，大概長這樣：

  [0.05540283, 0.04307444, 0.051385277, 0.06090132, 0.143254817, 0.050655052,  
 0.04222497, 0.048893178, 0.036884325, 0.012775138, 0.038525177, 0.0385151,   
 0.0085251377, 0.00239232, 0.092022022, 0.08191191, 0.02020221, 0.0737373122,   
 0.07438382, 0.024333644]

每行得到一組20個概率（和為1.0），表示基於其他列值（Number_Seasons、At_bats、Doubles、Triples、RBIs、Position等）該行對應每支球隊的概率。然後按這個概率分佈隨機選一支球隊，最可能的隊被選中頻率最高，但不總是它，這樣能保證生成數據的多樣性。

調節數據的真實度

上面代碼生成的數據可能跟原始數據匹配得很好，但是卻缺少變化，覆蓋不到生產環境可能出現的一些組合。有幾種辦法可以調節真實度和約束程度。可以換個比隨機森林更強或更弱的模型來生成預測，或者調它的超參數。比如隨機森林可以調樹的最大深度(max depth)。深度設得很淺會讓隨機森林更粗糙，更多按目標列的整體分佈來，不那麼強烈地依賴其他特徵。

調節加的抖動量也行。預測數值字段時，不要直接用隨機森林輸出的精確預測值，因為隨機森林預測的唯一值數量有限——它們受訓練時見過的數據限制，雖然實際上限制不算大但確實可能導致少數幾個值被反覆預測。上面代碼裏給預測加了些噪聲增加多樣性，這個量可以調大或調小。

預測分類字段時，用predict_proba()獲取每行每個可能類別的概率。但可以調整這些概率（類似大語言模型裏調温度參數），讓它更偏向最可能的類，或者讓各類概率更接近（允許代碼更頻繁選不太可能的類）。

還有一招是預測每個值時，不基於所有已生成特徵，而是隻用部分。用的特徵越多、它們跟當前列關聯越強，數據就越真實。

下面代碼演示了調節使用特徵數量的辦法。把前面部分代碼封裝成參數化函數，可以控制用多少前序特徵預測當前特徵的合適值。還能控制是用最左邊的還是最右邊的。比如員工費用表，生成金額（第7列）時已經選好了其他六列的值。預測金額可以用全部六個，也可以只用比如3個。如果用最左邊3個，就是基於員工ID、部門、賬户來預測金額。如果用最右邊3個，就是基於費用日期、提交日期、提交時間來預測（預測性肯定差很多）。

用不同參數多次調用這個函數能生成一批多樣化的數據集。其他變體，比如打亂列順序再調用（列順序可以在調用前shuffle），也能很好地增加測試集的多樣性。這裏假設包含真實數據的pandas數據框（叫df）已經創建好了。

 from sklearn.ensemble import RandomForestRegressor, RandomForestClassifier  
import matplotlib.pyplot as plt  
import seaborn as sns  

def generate_dataset(df, max_cols_used, use_left):  
    feature_0 = df.columns[0]   
    hist = np.histogram(df[feature_0], density=True)  
    bin_centers = [(x+y)/2 for x, y in zip(hist[1][:-1], hist[1][1:])]  
    p = [x/sum(hist[0]) for x in hist[0]]  
    vals = np.random.choice(bin_centers, p=p, size=len(df)).astype(int)  
    vals = [x + (((1.0 * np.random.random()) - 0.5) * df[feature_0].std())  
            for x in vals]  
    synth_data = []  
    synth_data.append(vals)  
    synth_cols = [feature_0]  

    for col_name in df.columns[1:]:  
        print(col_name, synth_cols, len(synth_data))  
        synth_df = pd.DataFrame(synth_data).T  
        synth_df.columns = synth_cols  

        # Trains the Random Forest using only a specified set of features  
        if use_left:   
            use_synth_cols = synth_cols[:max_cols_used]  
        else:  
            use_synth_cols = synth_cols[-max_cols_used:]  
      
        # The remainer of the code is the same as previously.  
        if col_name in num_features:   
            regr = RandomForestRegressor()  
            regr.fit(df[use_synth_cols], df[col_name])  
            pred = regr.predict(synth_df[use_synth_cols])  
            vals = [x + (((1.0 * np.random.random()) - 0.5) * pred.std())  
                    for x in pred]  
            synth_data.append(vals)  

        if col_name in cat_features:  
            clf = RandomForestClassifier()  
            clf.fit(df[use_synth_cols], df[col_name])  
            synth_data.append(clf.predict(synth_df[use_synth_cols]))  

        synth_cols.append(col_name)  
          
    synth_df = pd.DataFrame(synth_data).T  
    synth_df.columns = synth_cols  
    return synth_df  

 synth_df = generate_dataset(df, max_cols_used=2, use_left=False)

運行後繪製At_bats和RBI，結果如下：

At bats和RBIs。真實數據藍色，合成數據紅色。

可以看到，大體關係保留了，但不像基於全部前序特徵生成時那麼貼合。

高斯混合模型的應用

第二種方法基於高斯混合模型（GMM）。《Python中的異常值檢測》裏有詳細介紹GMM及其在異常檢測中的應用。這裏快速説一下：GMM描述數據的分佈，假設數據分佈在若干簇(cluster)中，每個簇有中心點、大小，可以用協方差矩陣表示。協方差矩陣描述數據的形狀，指定每個特徵的方差（假設全是數值數據）以及每對特徵間的協方差。

GMM假設每個簇內的數據在各維度上近似高斯分佈，但允許任意數量的簇，每個簇可以有任意大小。它還假設每個簇裏的數據分佈在超橢球(hyper-ellipse)內。也就是説簇內每個特徵可以有任意方差，每對特徵可以有任意相關度，但這些足以合理描述簇內數據的形狀。如果數據在一個或多個成型良好的簇裏，這個假設通常成立。即使簇不夠成型，也通常能細分成更小的簇讓每個都足夠規整。

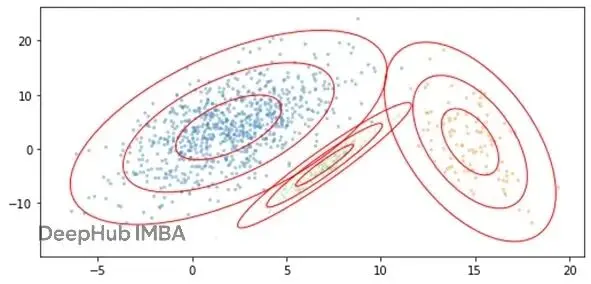
下面是一個2D數據集用GMM建模（3個簇）的例子：

這裏用不同顏色畫了三個簇，綠色最小，黃色次之，藍色最大。對數據空間的每個位置，可以算出數據點出現在那裏的可能性，等於它由藍色簇生成的可能性、綠色簇生成的可能性、黃色簇生成的可能性之和。

每個簇中心周圍的同心橢圓環代表距離中心那麼遠的位置被生成的概率（越靠近中心概率越高）。之所以是橢圓不是圓，因為GMM考慮數據的形狀（通過協方差矩陣）：某些特徵相關的話，簇往往呈現橢圓形而非圓形。

GMM假設數據在各簇中心周圍呈高斯分佈，所以靠近中心的區域比遠離中心的更密集，符合高斯分佈的特點。

靠近兩個或更多簇中心的位置，其他條件相同的話，比只靠近一個簇中心的位置更可能有數據。比如綠色簇左邊的位置比右邊更可能有數據，因為左邊的位置既可能由藍色簇生成，也可能由綠色簇生成。反之，綠色簇右邊的位置，被藍色簇（或黃色簇）生成的概率就低多了。

GMM常用於數據聚類和異常檢測。但它也是生成模型，因此很適合生成跟真實數據高度相似的數據。具體操作是先把GMM擬合到真實數據上，確定簇數量，以及每個簇的中心、大小（更準確説是簇權重——數據點由各簇生成的相對概率）和協方差矩陣。

之後GMM就能生成任意數量的新數據了（底層邏輯是每次生成一條記錄）。調用sample()方法就行。每條新記錄生成時，GMM先按權重隨機選一個簇，然後為該簇生成一個點。這類似於從簡單的1D高斯分佈採樣，但實際是從多元高斯分佈採樣。

下面代碼還是用棒球數據集

 import pandas as pd  
import numpy as np  
from sklearn.datasets import fetch_openml  
import matplotlib.pyplot as plt  
import seaborn as sns  
from sklearn.mixture import GaussianMixture  
from sklearn.ensemble import IsolationForest  

# Load the data  
data = fetch_openml('baseball', version=1, parser='auto')   
df = pd.DataFrame(data.data, columns=data.feature_names)  
df['Strikeouts'] = df['Strikeouts'].fillna(df['Strikeouts'].median())  

# Clean the data of strong outliers  
df = pd.get_dummies(df)  
np.random.seed(0)  
clf_if = IsolationForest()   
clf_if.fit(df)  
pred = clf_if.decision_function(df)  
trimmed_df = df.loc[np.argsort(pred)[50:]]  

# Determine the best number of clusters to use  
best_score = np.inf   
best_n_clusters = -1  
for n_clusters in range(2, 10):  
  gmm = GaussianMixture(n_components=n_clusters)  
  gmm.fit(trimmed_df)  
  score = gmm.bic(trimmed_df)  
  if score < best_score:  
    best_score = score  
    best_n_clusters = n_clusters  

# Fit a GMM  
gmm = GaussianMixture(n_components=best_n_clusters)   
gmm.fit(trimmed_df)  

# Use the GMM to generate synthetic data  
samples = gmm.sample(n_samples=500)   
synth_df = pd.DataFrame(samples[0], columns=df.columns)  

# Plot two columns as a 2d scatterplot  
sns.scatterplot(data=df, x="At_bats", y="RBIs", color='blue', alpha=0.1)  
sns.scatterplot(data=synth_df, x="At_bats", y="RBIs",  
color='red', marker="*", s=200)  
 plt.show()

跟逐列生成（對每列用預測器）一樣，用GMM生成的數據非常真實，特徵間的關聯關係保持得很好。下圖是用GMM生成的。

真實數據（藍點）和GMM生成的合成數據（紅星）的At_bats與RBIs

真實數據還是藍點，合成數據是紅星。合成數據遵循相同分佈，而且至少在這對特徵和生成的數量上，往往比部分真實數據還要"典型"。

處理分類數據的技巧

處理分類數據稍微麻煩些，因為GMM要求純數值數據，得先對分類列編碼。生成的合成行也全是數值，需要反向轉換，把GMM生成的數值轉回數據集原本用的分類值。

具體怎麼轉換取決於編碼方式。如果是獨熱編碼，就取值最高的那個二進制列作為生成的值；如果是計數編碼，就取計數最接近生成值的那個。其他編碼方式類似。

創建更多樣化的數據

這樣用GMM很適合生成真實數據，但不適合生成異常數據。如果想生成變化更大的數據，有幾種辦法。一種是修改各簇的協方差矩陣。Scikit-learn的GMM類（這裏用的）維護一個3D協方差數組，第一個維度對應簇，然後每個簇有一個2D矩陣。上面代碼選了9作為簇數，所以有9個2D協方差矩陣。每個是22×22，因為編碼後有22個特徵，矩陣存儲每對特徵間的協方差（主對角線是各特徵的方差）。

可以修改協方差讓值的範圍更大：

 for i in range(len(gmm.covariances_)):  
   for j in range(len(gmm.covariances_[i])):  
     for k in range(len(gmm.covariances_[i])):  
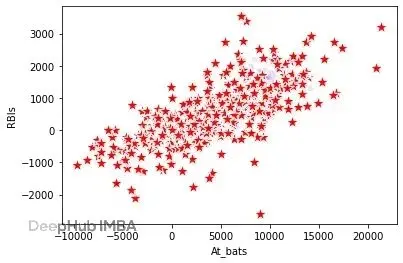
       gmm.covariances_[i][j][k] *= 20.0

這把每個簇協方差矩陣裏的每個值都乘以20.0；不同情況可能需要更小或更大的係數，這個可以調來生成一系列不同的測試數據集。生成結果如下：

合成數據（紅星）的範圍在各個方向上都比真實數據大得多，相對原始數據應該包含很大比例的異常值。

其他對數據空間密度建模的工具也能類似生成數據。比如scikit-learn的KernelDensity工作方式很像，也提供sample() API。多維直方圖這種方法也能對真實數據建模並生成匹配的合成數據。

評估生成數據的質量

首先得看數據，做點探索性數據分析(EDA)，看能不能發現明顯問題。還可以寫一些測試。一個簡單方法是訓練分類器看它能否正確區分真實數據和合成數據。如果用CatBoost這種強模型，它大部分情況下都分不出來，那合成數據質量應該不錯。理想情況是花時間調一下CatBoost模型，雖然CatBoost默認超參數已經挺強了。

另一個辦法是做異常檢測。在真實數據上訓練一兩個異常檢測器，然後用它們評估真實數據和合成數據，看合成數據是不是有更多異常值——以及是不是有比真實數據更極端的異常值。做這個的時候還應該做集體異常檢測(collective outlier detection)，不是檢查單個合成行是否真實，而是檢查它們整體作為一個集合是否合理。

總結

這裏只講了兩種生成合成數據的辦法：用預測模型逐單元格生成；用高斯混合模型(GMM)。其他方法還有很多，包括貝葉斯網絡、模擬、生成對抗網絡(GANs)、自編碼器、大語言模型(LLMs)等等。不過這兩種方法已經夠用了，實現直接、速度快、相對好理解，生成的合成數據跟原始真實數據的匹配度通常能滿足需求。

https://avoid.overfit.cn/post/46d206b780a844c0b9a72334a5f276da

作者：W Brett Kennedy