---

 

2. Find Max and Min

 

 

---

 

3. Matrix Search

這個問題有一個十分美好的前提，那就是我們所給的$n\times n$矩陣是行列皆有序的，在這樣的條件下，我們要尋找某個元素$x$在不在矩陣中，通過對手論證，我們可以做到線性時間$O(n)$。

 

首先是一個並不高效的方法，對每一行採用二分搜索，最多搜索$n$行，所以複雜度為$O(n\log n)$

 

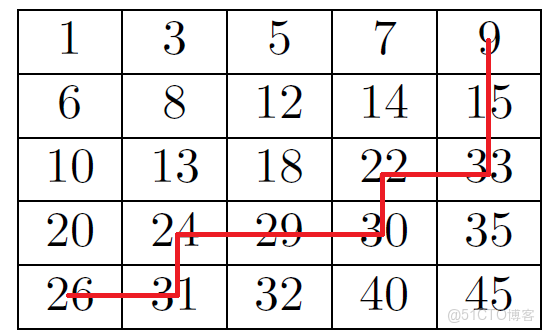
這裏有一個超級機智的算法，<Step-wise線性搜索>從右上角開始，每次將搜索值$x$與右上角的值比較，如果大於右上角的值，則直接去除1行，否則，則去掉1列。如下所示，展示了在矩陣中查找$x=28$的過程

 

 

在對手論證中，我們只需要儘可能的構造一個數去查找，但是總是不滿足條件，比如找不到的情況，就能達到最壞情況，而最短時間就是採用這種<Step-wise>方法了。這種查找方式最多也就是遍歷完兩遍對角線，總共的探查次數最多為$n+n-1=2n-1$，所以複雜度為$O(n)$。

 

---

 

4.

 

問題描述：有25匹賽馬，一片場地只有5條賽道，現在要求你用盡可能少的比賽場次來選出最快的前三名。

首先，至少每一匹馬都有機會去跑一遍，所以至少要先比賽5場，得出總共25匹馬的5個小組排名。接着，就是把每一組的冠軍拿出來遛遛，第6場過後，我們就能選出冠軍了，同時，我們也知道這第六場中的最後兩名一定不可能是前三名了，因為他們至少都要輸給已知的3匹馬。順帶着，這兩匹不可能的賽馬所在小組裏的馬廄都不可能了，想想小組第一都敗了。（咦，當年翁學姐小組第一但是沒出線就是這麼一回事兒啊！！！）那麼問題來了，下面只用一場比賽能夠搞定麼？答案是：可以！！

我們先給出競賽的情況，