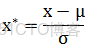歸一化

（1）什麼是歸一化？
        通俗理解，就是對原始數據進行線性變換把數據映射到[0, 1]區間。

具有的特點：
        1、對不同特徵維度進行伸縮變換。
        2、改變原始數據的分佈。使各個特徵維度對目標函數的影響權重是一致的（即使得那些扁平分佈的數據伸縮變換成類圓形）。
        3、對目標函數的影響體現在數值上 。
        4、把有量綱表達式變為無量綱表達式 。

（2）歸一化有什麼優點？
        A、使數據處理更加便捷、快速。
        B、把有量綱的數據變換為無量綱的純量，即使數據處於同一數量級，可以消除指標之間的量綱和量綱單位的影響，提高不同數據指標之間的可比性。
        C、提升模型的收斂速度。
        D、提升模型的精度。
        E、深度學習中數據歸一化可以防止模型梯度爆炸。

（3）歸一化有哪些缺點？
        A、最大值與最小值非常容易受異常點影響。
        B、魯棒性較差，只適合傳統精確小數據場景。

（4）歸一化有哪些方法？
        A、線性轉換，即min-max歸一化（常用方法）例如： y=(x-min)/(max-min)
        B、對數函數轉換，例如 y=log10(x)
        C、反餘切函數轉換， 例如 y=atan(x)*2/PI

標準化

（1）什麼是標準化？
通俗理解，把數據按比例縮放，使之落入一個小的空間裏。

具有的特點：對不同特徵維度的伸縮變換的目的是使得不同度量之間的特徵具有可比性。同時不改變原始數據的分佈。

（2）標準化有什麼優點？
1、不改變原始數據的分佈。保持各個特徵維度對目標函數的影響權重 。
2、對目標函數的影響體現在幾何分佈上 。
3、在已有樣本足夠多的情況下比較穩定，適合現代嘈雜大數據場景。

（3）標準化有哪些方法？
1、z-score標準化，經過處理後的數據均值為0，標準差為1。方法為：

其中，其中μ是樣本的均值， σ是樣本的標準差。這種標準化方法一般要求原始數據的分佈近似為高斯分佈（正太分佈），否則標準化的效果會變得很差。它們可以通過現有樣本進行估計，在已有樣本足夠多的情況下比較穩定，適合現代嘈雜大數據場景
2、小數定標標準化：通過移動X的小數位置來進行規範化，y= x/10的j次方(其中,j使得Max(|y|) <1的最小整數。
3、對數Logistic模式：新數據=1/（1+e^(-原數據)）。