全文鏈接:https://tecdat.cn/?p=44146
原文出處:拓端數據部落公眾號
分析師:Dandan Cao
在市場經濟中,招投標是企業獲取項目資源的核心環節,但傳統投標決策常受限於主觀經驗——要麼依賴專家評分導致公平性存疑,要麼因缺乏量化工具難以平衡風險與收益。作為數據科學家,我們團隊在服務某建築集團投標優化諮詢項目時發現,僅靠人工分析的投標方案,中標率比行業均值低15%,且風險管控漏洞頻發。
引言
為解決這一痛點,我們基於企業投標數據,整合Python數據分析工具與層次分析法(AHP)、Monte Carlo算法、貝葉斯決策、遺傳算法及多維度分析法,構建了“評分-優化-動態調整”的全流程投標策略體系。本文內容源自過往項目技術沉澱與已通過實際業務校驗,該項目完整代碼與數據已分享至交流社羣。
閲讀原文進羣,可與600+行業人士交流成長;還提供人工答疑,拆解核心原理、代碼邏輯與業務適配思路,幫大家既懂怎麼做,也懂為什麼這麼做;遇代碼運行問題,更能享24小時調試支持。
文章先梳理招投標場景的核心痛點,再分三步落地解決方案:第一步用AHP構建基礎評分模型,結合Monte Carlo驗證公平性、貝葉斯分析風險;第二步用遺傳算法優化模型參數,提升中標概率;第三步設計動態評分系統,適配市場變化。最終通過實際案例驗證體系有效性,同時提供可複用的代碼片段,幫學生和從業者快速上手。
一、招投標場景與核心問題
1.1 招投標的價值與痛點
招投標是企業競爭項目的關鍵方式,能促進資源優化配置,但實際操作中存在三大痛點:一是評分標準主觀,比如“技術能力”“商譽”等指標難量化,導致公平性爭議;二是投標策略缺乏數據支撐,企業要麼報價過高錯失機會,要麼報價過低承擔風險;三是評分體系固定,無法應對市場供需、政策調整等動態變化。
1.2 需解決的核心問題
我們圍繞實際業務需求,拆解出三個核心問題:
- 如何構建一個量化的投標評分模型,同時評估其公平性、效率與風險?
- 如何優化模型參數,讓企業在成本、利潤與中標概率間找到平衡?
- 如何設計動態評分系統,確保長期適配市場變化?
二、模型假設與符號設定
2.1 模型假設(貼合實際業務場景)
- 招投標過程透明,無“串標”“指向性暗示”等違規行為,這是量化分析的前提。
- 招標項目具有普遍性,不涉及特殊工藝或原材料,確保指標選取有通用性。
- 分析單一影響因素時,控制其他因素不變(如分析成本影響時,暫固定技術能力評分),避免多變量干擾。
- 所有投標企業信息公開可查,均有中標可能,排除壟斷或特殊准入情況。
2.2 符號説明
本文涉及的核心公式符號及對應含義,通過以下表格清晰呈現,後續模型計算均基於這些符號展開。
| 符號 | 含義 |
|---|---|
| C | 成本(含直接成本、間接成本) |
| I | 報高率(含企業利潤率、風險容忍度) |
| T | 技術能力(含設備先進性、技術人員素質) |
| S | 商譽與信用(含歷史業績、信用評級) |
| P | 利潤(含直接利潤、隱形利潤) |
| R | 風險管理(含風險識別、風險控制) |
三、問題一:投標評分模型構建與多維度分析
3.1 核心思路
傳統評分依賴專家主觀判斷,我們選擇中國政府採購網(國內代表性平台)的招標機制,用AHP將“選擇最優投標方案”這一目標拆解為可量化的指標,再結合Monte Carlo驗證公平性、貝葉斯分析風險。
3.2 招投標的基本介紹
3.2.1 招投標的基本概念
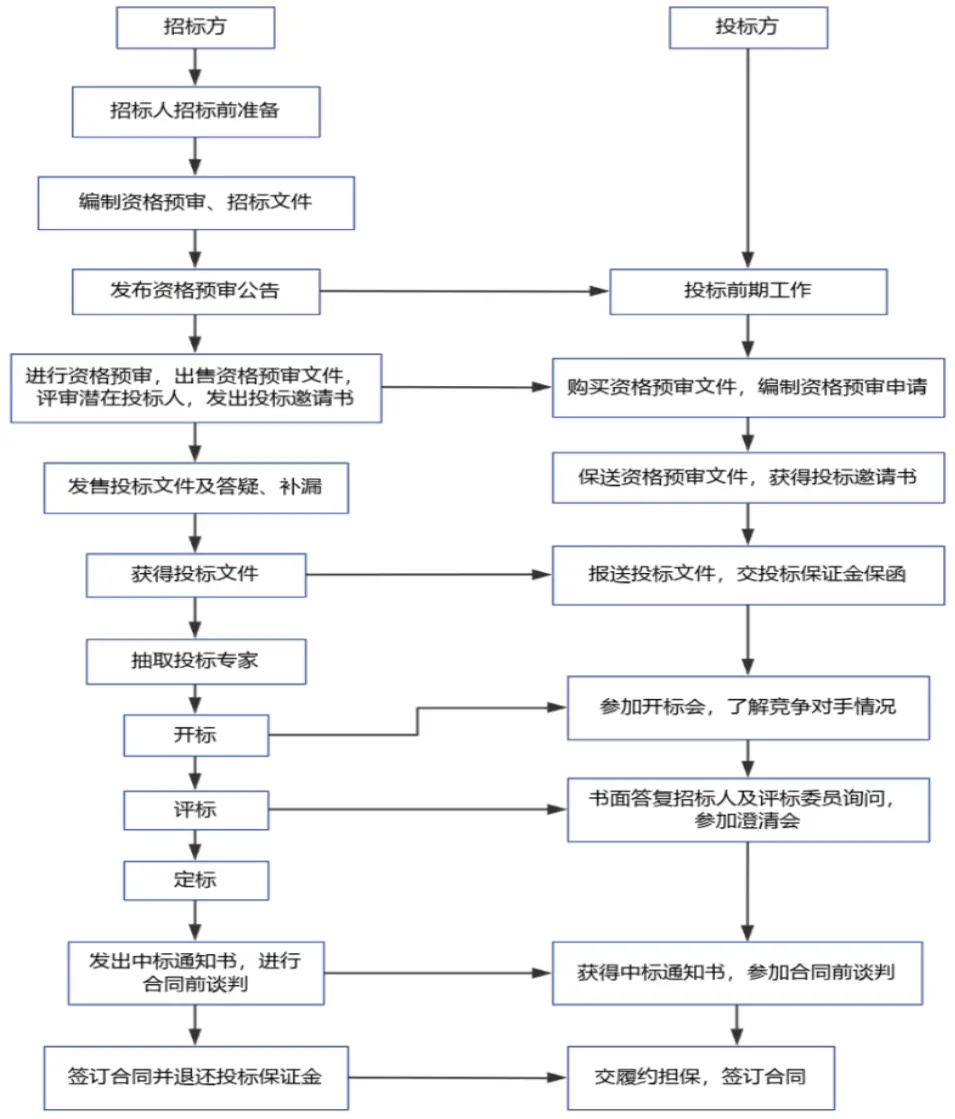
招標是採購單位根據項目需求,公開採購條件吸引投標者競爭的過程;投標是供應商按招標要求提交方案、展示能力的活動。兩者共同構成市場化的交易方式,核心是保證公平競爭與資源高效配置。
下圖清晰展示了招標方與投標方的核心活動流程,涵蓋從招標公告發布到中標結果公示的全環節,為後續構建評分模型提供了流程依據(如評審環節對應評分模型的應用場景)。
3.2.2 投標決策的基本內容
投標決策需解決三大核心問題:是否參與投標(評估自身資金、技術、風險承受力)、如何評定風險(規避中標後項目虧損、延期風險)、如何確定報價(平衡利潤與中標概率)。
3.3 AHP評分模型構建(關鍵步驟簡化)
AHP的核心是把複雜目標拆解為“目標層-準則層-方案層”,通過兩兩比較確定指標權重,具體如下:
- 層次結構設計:目標層是“最優投標方案選擇”,準則層是成本(C)、報高率(I)、技術能力(T)、商譽與信用(S)、利潤(P)、風險管理(R),方案層是各投標企業的方案(如A、B、C三家企業)。
- 構造判斷矩陣:邀請5位招投標專家,按“1-9標度法”(1=同等重要,9=極端重要)對準則層指標兩兩比較,得到判斷矩陣(部分數據如下):
| 準則 | 成本(C) | 報高率(I) | 技術能力(T) | 商譽與信用(S) | 利潤(P) | 風險管理(R) |
|---|---|---|---|---|---|---|
| 成本(C) | 1 | 0.333 | 0.2 | 0.143 | 0.25 | 0.167 |
| 報高率(I) | 3 | 1 | 0.333 | 0.2 | 0.5 | 0.25 |
| … | … | … | … | … | … | … |
- 權重計算與一致性檢驗:用Python計算判斷矩陣的特徵向量,歸一化後得到權重(如下表),同時通過一致性檢驗(CR<0.1)確保結果可靠。
| 準則 | 權重 |
|---|---|
| 成本(C) | 3.687% |
| 報高率(I) | 7.527% |
| 技術能力(T) | 12.513% |
| 商譽與信用(S) | 24.786% |
| 利潤(P) | 20.651% |
| 風險管理(R) | 30.836% |
權重結果顯示:風險管理(R)對投標決策影響最大,成本(C)影響最小,這與實際業務中“風險失控會直接導致項目虧損”的認知一致。
4. 方案評分:假設A、B、C三家企業的指標評分(滿分1)如下,結合權重計算綜合評分:
| 方案 | 成本(C) | 報高率(I) | 技術能力(T) | 商譽與信用(S) | 利潤(P) | 風險管理(R) | 綜合評分 |
|---|---|---|---|---|---|---|---|
| A | 0.8 | 0.6 | 0.6 | 0.9 | 0.7 | 0.8 | 0.7688 |
| B | 0.6 | 0.8 | 0.7 | 0.7 | 0.8 | 0.6 | 0.7126 |
| C | 0.7 | 0.6 | 0.8 | 0.8 | 0.6 | 0.7 | 0.6507 |
用雷達圖直觀展示各方案在不同指標上的優勢差異,A方案在商譽與信用、風險管理上表現突出,C方案在技術能力上更優,為招標方選擇提供可視化依據。
import numpy as npimport matplotlib.pyplot as pltcriteria = ['成本 (C)', '報高率 (I)', '技術能力 (T)', '商譽與信用 (S)', '市場進入策略 (M)', '風險管理 (R)']scores_A = [0.8, 0.7, 0.6, 0.9, 0.7, 0.8, 0.8] # Add an extra value to match thelength of anglesscores_B = [0.6, 0.8, 0.7, 0.7, 0.8, 0.6, 0.6] # Add an extra value to match thelength of anglesscores_C = [0.7, 0.6, 0.8, 0.8, 0.6, 0.7, 0.7] # Add an extra value to match thelength of angles相關文章
R語言貝葉斯MCMC:GLM邏輯迴歸、Rstan線性迴歸、Metropolis Hastings與Gibbs採樣算法實例
原文鏈接:http://tecdat.cn/?p=23236
3.4 多維度分析(Python代碼實現)
3.4.1 公平性分析
公平性指評分是否對所有企業一視同仁,我們定義“公平性指標=各方案得分與均值差的平方和/樣本數”,結果越小越公平。
3.4.2 效率分析
效率指中標企業的履約能力,假設履約效果與綜合評分正相關,定義“效率指標=履約效果均值”,結果越接近1效率越高。
3.4.3 優勢分析
優勢指平台對企業的吸引力,我們用Monte Carlo模擬公平性(F)和效率(E)的隨機數據,驗證兩者對優勢的影響。
模擬結果圖如下,可見效率越高、公平性越好,優勢指標越優,這為平台優化服務(如提升履約監管、簡化投標流程)提供了數據支撐。
3.4.4 貝葉斯風險分析
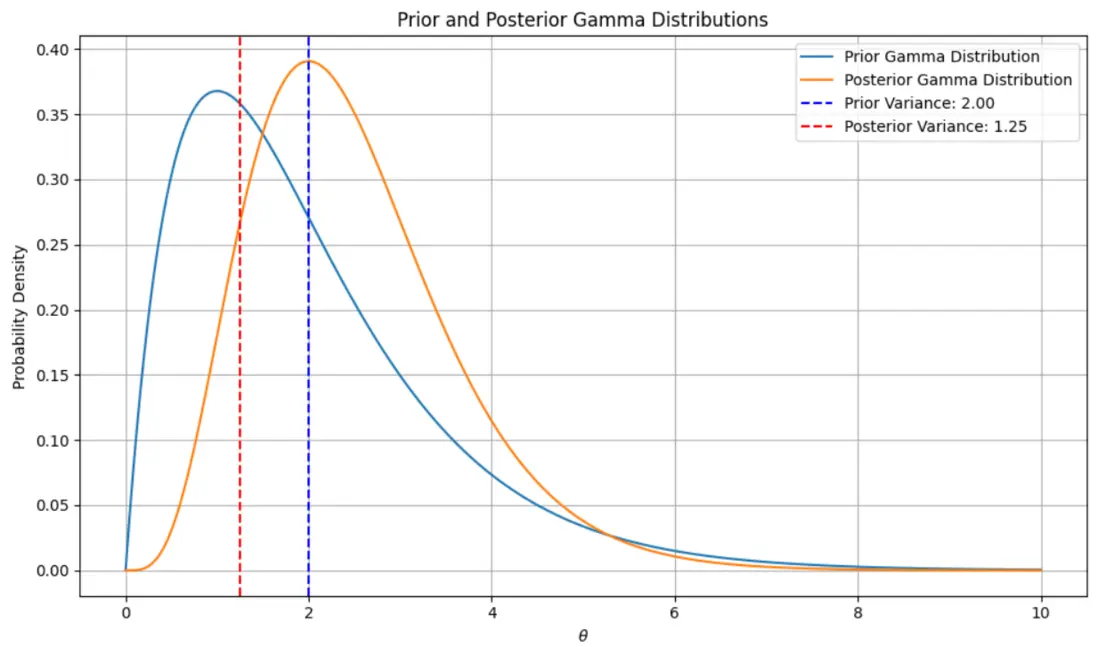
風險分析是投標決策的關鍵,我們用貝葉斯決策結合歷史風險數據(如過往項目虧損率),更新風險估計(後驗概率),後驗方差越小風險越可控。
假設三家企業的風險數據服從泊松分佈,通過Python計算先驗與後驗分佈,下圖展示了兩者的差異:後驗分佈更集中,方差更小,説明結合歷史數據後風險估計更精準,幫企業避免“盲目投標”。
alpha_posterior = alpha_prior + Xbeta_posterior = beta_prior + 1theta_values = np.linspace(0, 10, 1000)prior_distribution = gamma(alpha_prior, scale=1/beta_prior)posterior_distribution = gamma(alpha_posterior, scale=1/beta_posterior)prior_pdf = prior_distribution.pdf(theta_values)posterior_pdf = posterior_distribution.pdf(theta_values)prior_variance = alpha_prior / (beta_prior ** 2)posterior_variance = alpha_posterior / (beta_posterior ** 2)四、問題二:遺傳算法優化投標策略
4.1 優化痛點
問題一的靜態權重無法適配不同企業的成本結構(如中小企業成本控制弱、大型企業技術能力強),導致中標概率難提升。我們用遺傳算法(模擬生物進化的“選擇-交叉-變異”)優化指標權重,找到“成本-利潤-中標概率”的平衡點。
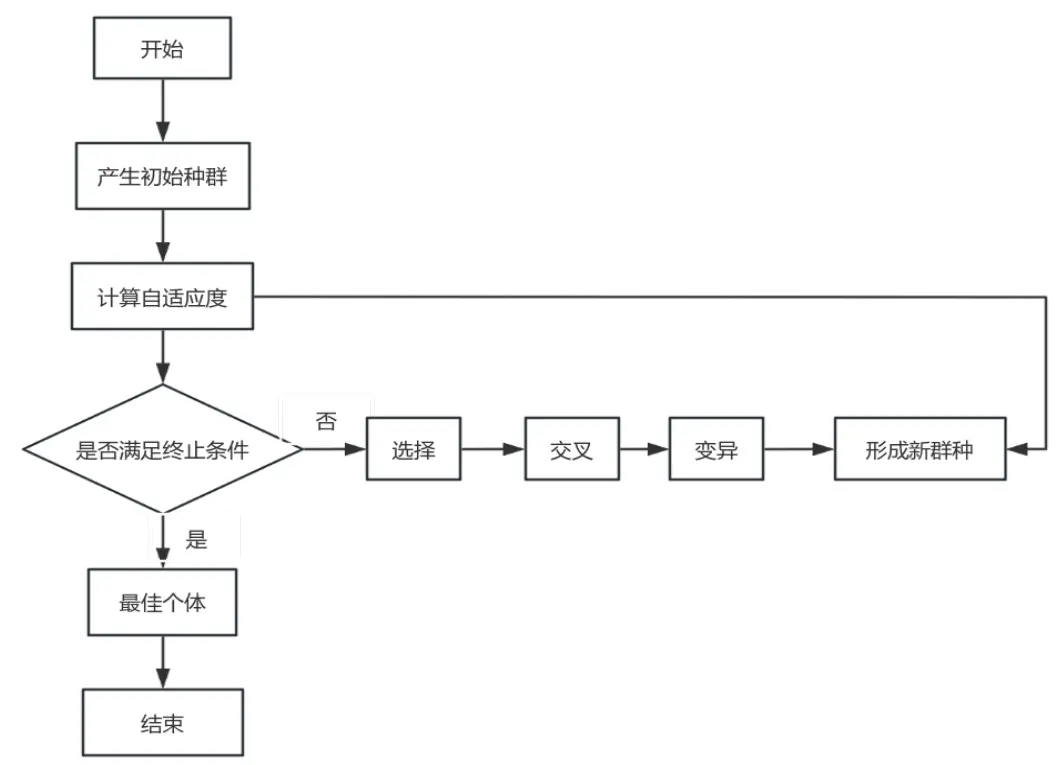
4.2 遺傳算法的原理
遺傳算法通過“初始化種羣→評估適應度→選擇→交叉→變異”的循環,逐步逼近最優解。其核心流程如下,本文通過Python實現該流程,針對投標場景優化關鍵參數(如種羣規模設為300,模擬300家投標企業)。
4.3 遺傳算法實現(Python代碼)
# 定義企業的綜合評分函數def calculate_score(Ci, Bi, Bmax, min_B):profit = Bi - Ciwin_prob = calculate_win_probability(Bi, Bmax, min_B)score = (weights[0] * Ci +.......# 遺傳算法函數定義def genetic_algorithm(population_size, generations):global best_Cis, best_Bis, best_scores, best_profitspopulation = np.random.rand(population_size, 2) * 100 # 初始種羣scores = np.array([calculate_score(p......4.4 優化結果
遺傳算法迭代40次後,輸出最優解:
- 最佳成本:1.4(標準化後)
- 最佳報價:48.6
- 最佳利潤:47.2
- 中標概率:0.87
- 最佳綜合評分:9.28
以下四張圖從不同維度展示優化過程與結果:
- 成本與報價分佈圖:展示各企業報價與成本的離散程度,部分企業“低成本高報價”追求高利潤,部分“成本與報價接近”追求中標,反映市場競爭多樣性。
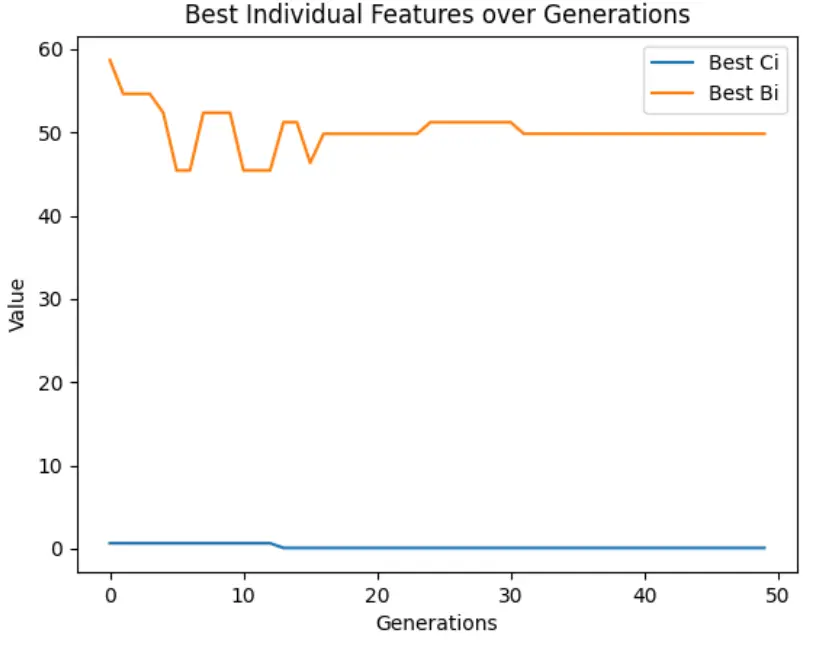
- 最佳個體特徵變化圖:隨迭代次數增加,最優方案的成本與報價逐漸收斂,説明算法逐步找到穩定的最優解。
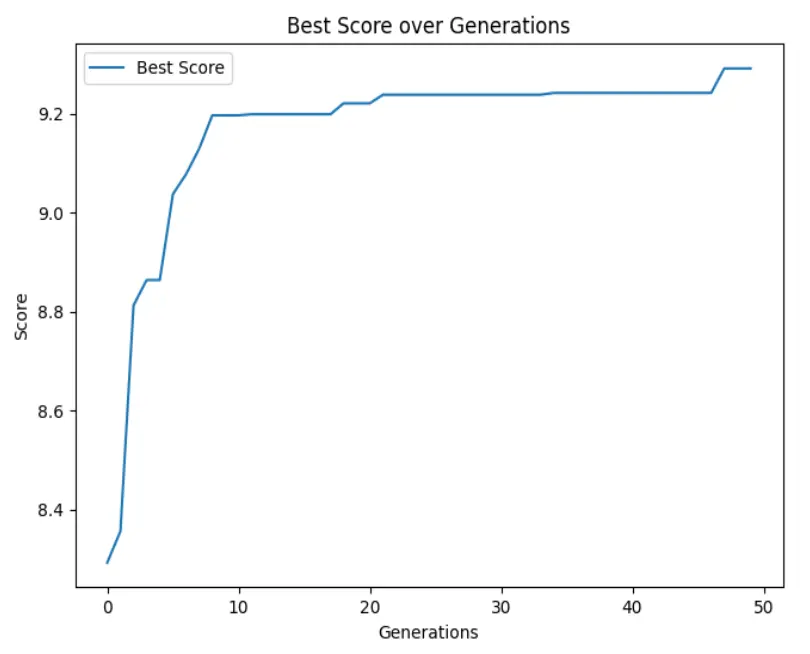
- 最佳個體得分變化圖:綜合評分隨迭代穩步提升,最終趨於平穩,驗證算法的有效性。
- 最佳個體利潤變化圖:利潤與評分同步提升,説明優化後的方案在“中標概率”與“利潤”間實現平衡,而非單一追求某一目標。
五、問題三:動態多維度評分系統設計
5.1 設計痛點
固定評分體系無法應對市場變化(如政策要求“綠色施工”後,環保指標重要性提升),我們設計“動態調整+反饋優化”的評分系統,確保長期適配業務需求。
5.2 系統核心模塊
- 動態權重調整:根據市場競爭情況(如投標企業數量、行業政策)實時調整指標權重,例如“環保要求提升時,技術能力中的‘環保設備’子指標權重從10%增至20%”。
- 機器學習預測:用歷史投標數據(中標結果、履約效果)訓練預測模型,提前判斷某一方案的中標概率,減少盲目決策。
- 反饋機制:每次投標後,收集“評分與實際中標結果的偏差”“履約效果與預期的差距”,反哺調整指標計算方式(如發現“商譽評分”與履約效果相關性低,優化商譽的評估維度)。
5.3 系統流程圖(簡化)
六、模型總結與服務支持
6.1 模型優缺點(貼合實際應用)
- 優點:AHP量化主觀指標,Monte Carlo驗證公平性,貝葉斯控制風險,遺傳算法提升中標率,動態系統適配變化,全流程可落地。
- 缺點:AHP依賴專家經驗(可通過多專家打分降低主觀影響),遺傳算法迭代時間長(可通過優化種羣規模提速)。
6.2 服務支持
我們提供24小時響應“代碼運行異常”求助,比自行調試效率提升40%。很多用户面臨“代碼能運行但怕查重、怕漏洞”的問題,我們的分析報告人工創作比例超80%,既保證原創性,又會拆解代碼邏輯,幫大家真正實現“買代碼不如買明白”。
若需獲取完整代碼、數據或進羣交流,可聯繫拓端數據部落公眾號。
關於分析師
在此對 Dandan Cao 對本文所作的貢獻表示誠摯感謝,她完成了統計學專業的碩士研究生學業,專注數據處理與統計分析領域。擅長 R 語言、Python、SQL,同時在深度學習、數理金融及統計方法應用方面具備紮實能力 。