為什麼 shift 比 pop 慢？JS 中隊列的實現詳情 - javascript,前端,隊列,shift,pop 清隆動態日志

我們知道在 JS 中，刪除數組元素有兩個方法：pop 與 shift，分別可以刪除末尾與開頭的元素。

然而同樣是刪除元素，它們的執行時間確實不同的。

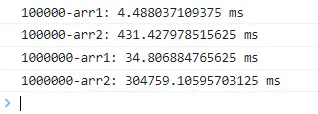
當數組項目較多時，shift 的執行時間明顯長於 pop。

const test = (arrLength) => {
  let arr1 = []
  console.time(`${arrLength}-arr1`)
  for (let i = 0; i < arrLength; i++) {
    arr1.push(i)
  }
  for (let i = 0; i < arrLength; i++) {
    arr1.pop()
  }
  console.timeEnd(`${arrLength}-arr1`)

  let arr2 = []
  console.time(`${arrLength}-arr2`)
  for (let i = 0; i < arrLength; i++) {
    arr2.push(i)
  }
  for (let i = 0; i < arrLength; i++) {
    arr2.shift()
  }
  console.timeEnd(`${arrLength}-arr2`)
}

test(10 ** 5)
test(10 ** 6)

結果如下：

這是因為 pop 刪除元素後不需要改變其他元素的索引，時間複雜度為 O(1)；而調用 shift 方法刪除開頭元素後，需要維護數組的索引，相當於對數組中的所有元素都進行了一次賦值操作，其時間複雜度為 O(n)

棧與隊列

棧與隊列是我們常用的兩種數據結構。

棧的元素先進後出，比如函數棧，函數遞歸調用時，後調用的函數先執行完。

隊列的元素先進先出，比如任務隊列，任務按照派發的順序依次執行。

在 JS 中，棧可以看成只調用 push 與 pop 方法的數組，隊列可以看成是隻調用 shift 與 push 方法的數組。

然而在之前的例子中也看到了，當處理大量數據時，把數組直接當成隊列使用性能非常差。

所以，我們要設法實現隊列這一數據結構。

如何實現？

開始之前我們要明確實現的目標，我們實現的隊列要提供以下幾個功能：

存儲數據：隊列要能夠按序存儲數據
push：添加元素的唯一方法，將元素添加進隊列尾部的方法，並返回隊列長度
shift：刪除元素的唯一方法，將隊首元素刪除的方法，並返回刪除的元素
length：可以通過 length 屬性訪問隊列的長度
訪問元素：一般隊列會允許訪問隊頭與隊尾的元素

這裏介紹通過 假刪除數組元素 的方式實現隊列。

我們知道數組的不能當作隊列使用的原因是直接使用 shift 刪除元素後會移動其餘元素的索引。

我們可以自己維護數組的索引，避免刪除後頻繁移動。

具體實現是定義一個 offset 變量，記錄索引的偏移。

在訪問元素時，通過偏移量的計算，獲取正確的結果。

在刪除元素時，只用把數組首元素置空，然後偏移加 1。

這期間不進行真實的刪除操作，這就是所謂的假刪除。

但為了避免數組大小無限增大，我們設置當偏移量(空元素)大於數組的長度的一半時，就將空元素刪除，保證佔用空間不超過使用隊列大小的兩倍。

具體實現代碼及註釋如下

// 創建一個隊列
function createQueue() {
  const arr = [] // 內部的數組
  let offset = 0 // 偏移

  // 添加元素，返回隊列的長度
  const push = (...arg) => {
    return arr.push(...arg) - offset
  }
  // 刪除元素，返回被刪除的元素
  const shift = () => {
    const res = arr[offset] // 要返回的刪除元素
    // 假刪除
    arr[offset] = undefined
    offset++

    // 避免數組無限擴大，定期一次性刪除前面的空元素
    if (offset > arr.length / 2) {
      arr.splice(0, offset)
      offset = 0
    }

    return res
  }

  // 通過 Proxy 攔截隊列的操作
  const p = new Proxy(
    {},
    {
      get(target, prop) {
        switch (prop) {
          case 'push': {
            return push
          }
          case 'shift': {
            return shift
          }
          case 'length': {
            // 隊列長度 = 數組實際長度 - 偏移
            return arr.length - offset
          }
          default: {
            // 元素真實索引 = 要訪問的索引 + 偏移
            return arr[Number(prop) + offset]
          }
        }
      },
    }
  )

  return p
}

const queue = createQueue()

console.log(queue.push(0, 1, 2, 3, 4)) // 5
console.log(queue[0]) // 0
console.log(queue.length) // 5

console.log(queue.shift()) // 0
console.log(queue[0]) // 1
console.log(queue.length) // 4

console.log(queue.shift()) // 1
console.log(queue.push(5)) // 4
console.log(queue[0]) // 2
console.log(queue[queue.length - 1]) // 5

測試性能

進行 10/100/1000 萬次增刪操作，測試隊列的性能

const test = (arrLength) => {
  let arr1 = []
  console.time(`${arrLength}-arr1`)
  for (let i = 0; i < arrLength; i++) {
    arr1.push(i)
  }
  for (let i = 0; i < arrLength; i++) {
    arr1.pop()
  }
  console.timeEnd(`${arrLength}-arr1`)

  let arr2 = createQueue()
  console.time(`${arrLength}-arr2`)
  for (let i = 0; i < arrLength; i++) {
    arr2.push(i)
  }
  for (let i = 0; i < arrLength; i++) {
    arr2.shift()
  }
  console.timeEnd(`${arrLength}-arr2`)
}

test(10 ** 5)
test(10 ** 6)
test(10 ** 7)

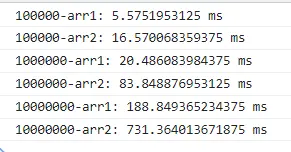
function createQueue() {……}

測量結果如下：