【數據結構與算法】初識算法詳情 - java,算法,數據結構,leetcode,leetcode算法程序員波特動態日志

1.1 什麼是算法？

定義

在數學和計算機科學領域，算法是一系列有限的嚴謹指令，通常用於解決一類特定問題或執行計算

In mathematics and computer science, an algorithm (/ˈælɡərɪðəm/) is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation.¹

Introduction to Algorithm²

不正式的説，算法就是任何定義優良的計算過程：接收一些值作為輸入，在有限的時間內，產生一些值作為輸出。

Informally, an algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output in a finite amount of time.

1.2 什麼是數據結構？

定義

在計算機科學領域，數據結構是一種數據組織、管理和存儲格式，通常被選擇用來高效訪問數據

In computer science, a data structure is a data organization, management, and storage format that is usually chosen for efficient access to data

Introduction to Algorithm²

數據結構是一種存儲和組織數據的方式，旨在便於訪問和修改

A data structure is a way to store and organize data in order to facilitate access and modifications

可以説，程序 = 數據結構 + 算法，它們是每一位程序員的基本功，下來我們通過對一個非常著名的二分查找算法的講解來認識一下算法

1.3 二分查找 ³

二分查找算法也稱折半查找，是一種非常高效的工作於有序數組的查找算法。後續的課程中還會學習更多的查找算法，但在此之前，不妨用它作為入門。

1) 基礎版

需求：在有序數組 $A$ 內，查找值 $target$

如果找到返回索引
如果找不到返回 $-1$

算法描述


前提	給定一個內含 $n$ 個元素的有序數組 $A$，滿足 $A_{0}\leq A_{1}\leq A_{2}\leq \cdots \leq A_{n-1}$，一個待查值 $target$
1	設置 $i=0$，$j=n-1$
2	如果 $i \gt j$，結束查找，沒找到
3	設置 $m = floor(\frac {i+j}{2})$ ，$m$ 為中間索引，$floor$ 是向下取整（$\leq \frac {i+j}{2}$ 的最小整數）
4	如果 $target < A_{m}$ 設置 $j = m - 1$，跳到第2步
5	如果 $A_{m} < target$ 設置 $i = m + 1$，跳到第2步
6	如果 $A_{m} = target$，結束查找，找到了

P.S.

對於一個算法來講，都有較為嚴謹的描述，上面是一個例子

後續講解時，以簡明直白為目標，不會總以上面的方式來描述算法

java 實現

public static int binarySearch(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {            // 在左邊
            j = m - 1;
        } else if (a[m] < target) {        // 在右邊
            i = m + 1;
        } else {
            return m;
        }
    }
    return -1;
}

$i,j$ 對應着搜索區間 $[0,a.length-1]$（注意是閉合的區間），$i<=j$ 意味着搜索區間內還有未比較的元素，$i,j$ 指向的元素也可能是比較的目標
- 思考：如果不加 $i==j$ 行不行？
- 回答：不行，因為這意味着 $i,j$ 指向的元素會漏過比較
$m$ 對應着中間位置，中間位置左邊和右邊的元素可能不相等（差一個），不會影響結果
如果某次未找到，那麼縮小後的區間內不包含 $m$

2) 改變版

另一種寫法

public static int binarySearch(int[] a, int target) {
    int i = 0, j = a.length;
    while (i < j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {            // 在左邊
            j = m;
        } else if (a[m] < target) {        // 在右邊
            i = m + 1;
        } else {
            return m;
        }
    }
    return -1;
}

$i,j$ 對應着搜索區間 $[0,a.length)$（注意是左閉右開的區間），$i<j$ 意味着搜索區間內還有未比較的元素，$j$ 指向的一定不是查找目標
- 思考：為啥這次不加 $i==j$ 的條件了？
- 回答：這回 $j$ 指向的不是查找目標，如果還加 $i==j$ 條件，就意味着 $j$ 指向的還會再次比較，找不到時，會死循環
如果某次要縮小右邊界，那麼 $j=m$，因為此時的 $m$ 已經不是查找目標了

1.4 衡量算法好壞

時間複雜度

下面的查找算法也能得出與之前二分查找一樣的結果，那你能説出它差在哪裏嗎？

public static int search(int[] a, int k) {
    for (
        int i = 0;
        i < a.length;
        i++
    ) {
        if (a[i] == k) {
            return i;
        }
    }
    return -1;
}

考慮最壞情況下（沒找到）例如 [1,2,3,4] 查找 5

int i = 0 只執行一次
i < a.length 受數組元素個數 $n$ 的影響，比較 $n+1$ 次
i++ 受數組元素個數 $n$ 的影響，自增 $n$ 次
a[i] == k 受元素個數 $n$ 的影響，比較 $n$ 次
return -1，執行一次

粗略認為每行代碼執行時間是 $t$，假設 $n=4$ 那麼

總執行時間是 $(1+4+1+4+4+1)*t = 15t$
可以推導出更一般地公式為，$T = (3*n+3)t$

如果套用二分查找算法，還是 [1,2,3,4] 查找 5

public static int binarySearch(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {            // 在左邊
            j = m - 1;
        } else if (a[m] < target) {        // 在右邊
            i = m + 1;
        } else {
            return m;
        }
    }
    return -1;
}

int i = 0, j = a.length - 1 各執行 1 次
i <= j 比較 $floor(\log_{2}(n)+1)$ 再加 1 次
(i + j) >>> 1 計算 $floor(\log_{2}(n)+1)$ 次
接下來 if() else if() else 會執行 $3* floor(\log_{2}(n)+1)$ 次，分別為
- if 比較
- else if 比較
- else if 比較成立後的賦值語句
return -1，執行一次

結果：

總執行時間為 $(2 + (1+3) + 3 + 3 * 3 +1)*t = 19t$
更一般地公式為 $(4 + 5 * floor(\log_{2}(n)+1))*t$

注意：

左側未找到和右側未找到結果不一樣，這裏不做分析

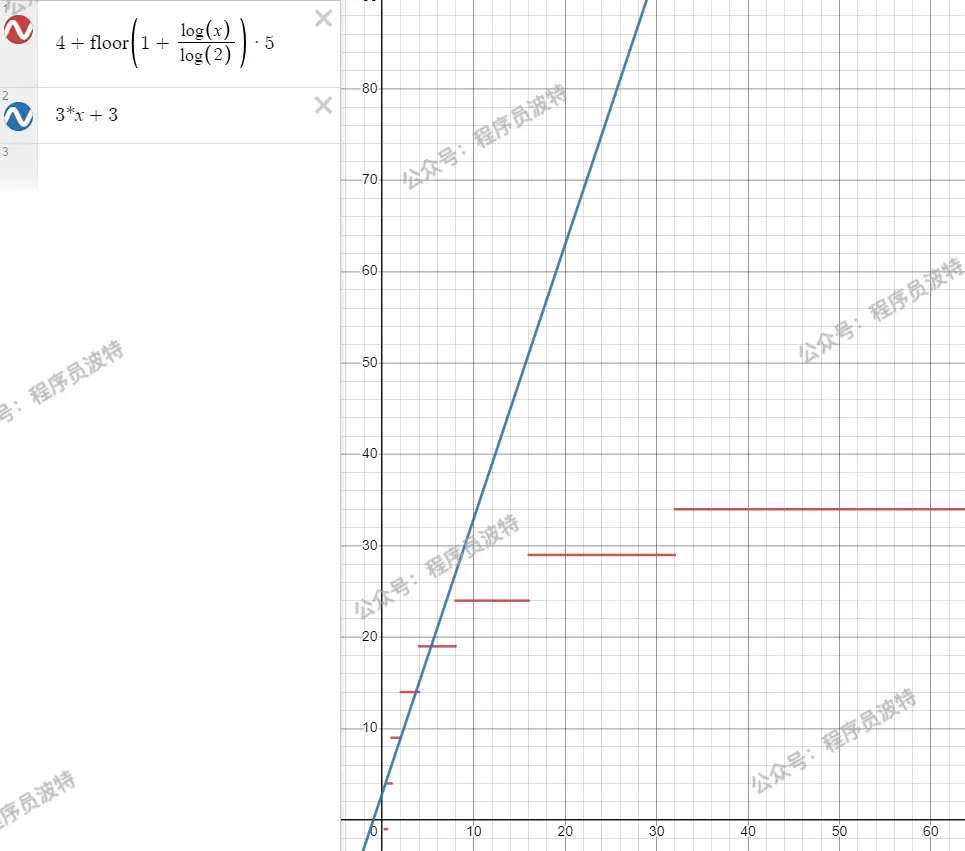
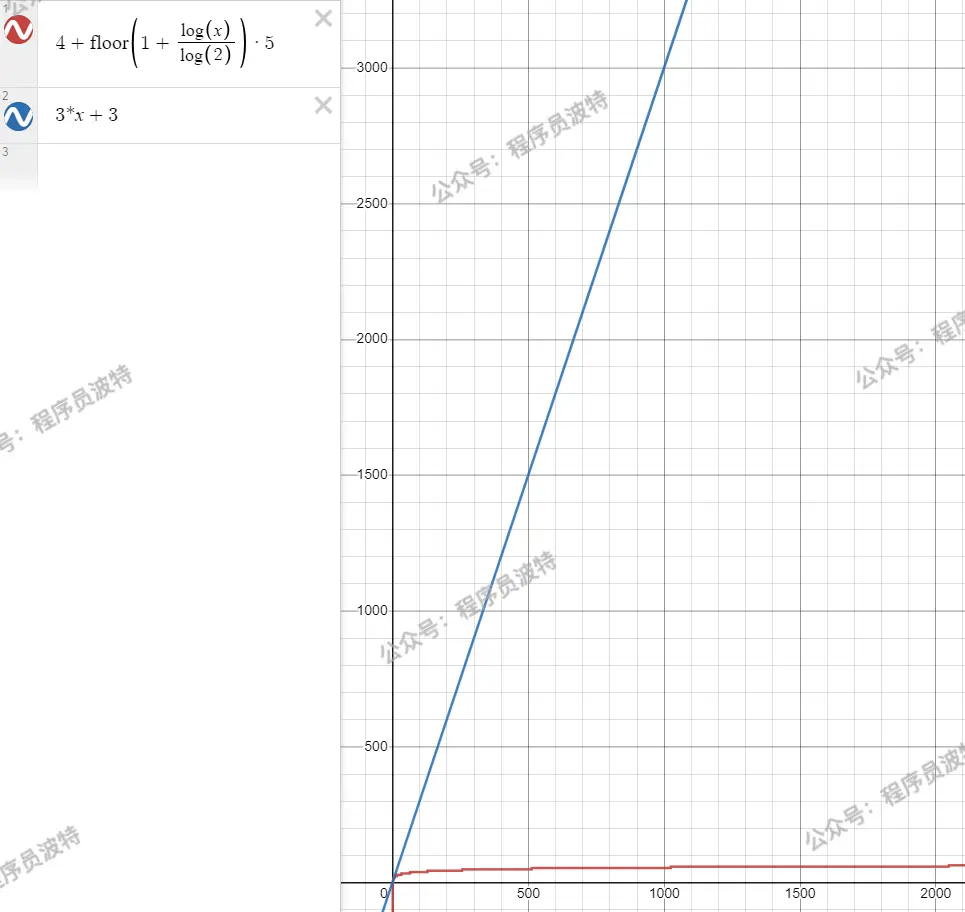
兩個算法比較，可以看到 $n$ 在較小的時候，二者花費的次數差不多

file

但隨着 $n$ 越來越大，比如説 $n=1000$ 時，用二分查找算法（紅色）也就是 $54t$，而藍色算法則需要 $3003t$

file

畫圖採用的是 Desmos | 圖形計算器

計算機科學中，時間複雜度是用來衡量：一個算法的執行，隨數據規模增大，而增長的時間成本

不依賴於環境因素

如何表示時間複雜度呢？

假設算法要處理的數據規模是 $n$，代碼總的執行行數用函數 $f(n)$ 來表示，例如：
- 線性查找算法的函數 $f(n) = 3*n + 3$
- 二分查找算法的函數 $f(n) = (floor(log_2(n)) + 1) * 5 + 4$
為了對 $f(n)$ 進行化簡，應當抓住主要矛盾，找到一個變化趨勢與之相近的表示法

大 $O$ 表示法⁴

file

其中

$c, c_1, c_2$ 都為一個常數
$f(n)$ 是實際執行代碼行數與 n 的函數
$g(n)$ 是經過化簡，變化趨勢與 $f(n)$ 一致的 n 的函數

漸進上界

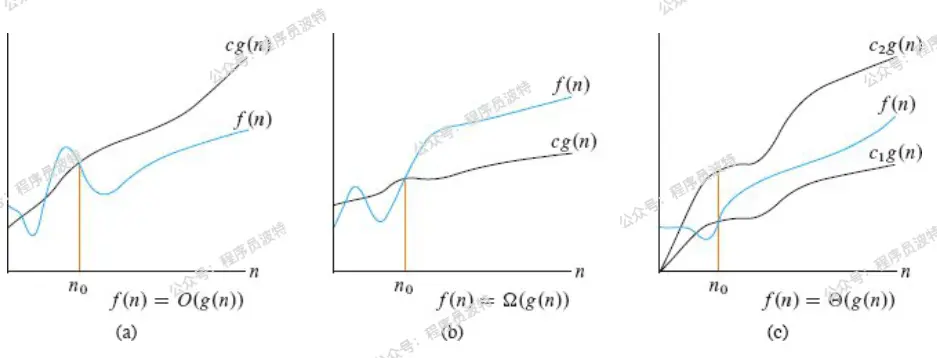
漸進上界（asymptotic upper bound）：從某個常數 $n_0$開始，$c*g(n)$ 總是位於 $f(n)$ 上方，那麼記作 $O(g(n))$

代表算法執行的最差情況

例1

$f(n) = 3*n+3$
$g(n) = n$
取 $c=4$，在$n_0=3$ 之後，$g(n)$ 可以作為 $f(n)$ 的漸進上界，因此表示法寫作 $O(n)$

例2

$f(n) = 5*floor(log_2(n)) + 9$
$g(n) = log_2(n)$
$O(log_2(n))$

已知 $f(n)$ 來説，求 $g(n)$

表達式中相乘的常量，可以省略，如
- $f(n) = 100*n^2$ 中的 $100$
多項式中數量規模更小（低次項）的表達式，如
- $f(n)=n^2+n$ 中的 $n$
- $f(n) = n^3 + n^2$ 中的 $n^2$
不同底數的對數，漸進上界可以用一個對數函數 $\log n$ 表示
- 例如：$log_2(n)$ 可以替換為 $log_{10}(n)$，因為 $log_2(n) = \frac{log_{10}(n)}{log_{10}(2)}$，相乘的常量 $\frac{1}{log_{10}(2)}$ 可以省略
類似的，對數的常數次冪可省略
- 如：$log(n^c) = c * log(n)$

常見大 $O$ 表示法

file

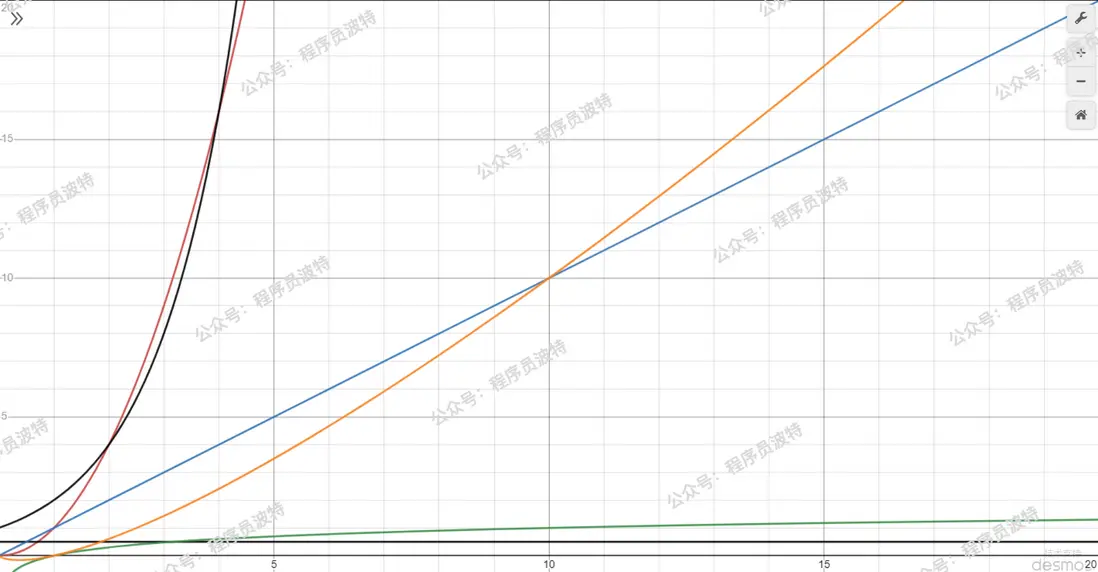
按時間複雜度從低到高

黑色橫線 $O(1)$，常量時間，意味着算法時間並不隨數據規模而變化
綠色 $O(log(n))$，對數時間
藍色 $O(n)$，線性時間，算法時間與數據規模成正比
橙色 $O(n*log(n))$，擬線性時間
紅色 $O(n^2)$ 平方時間
黑色朝上 $O(2^n)$ 指數時間
沒畫出來的 $O(n!)$

漸進下界

漸進下界（asymptotic lower bound）：從某個常數 $n_0$開始，$c*g(n)$ 總是位於 $f(n)$ 下方，那麼記作 $\Omega(g(n))$

漸進緊界

漸進緊界（asymptotic tight bounds）：從某個常數 $n_0$開始，$f(n)$ 總是在 $c_1*g(n)$ 和 $c_2*g(n)$ 之間，那麼記作 $\Theta(g(n))$

空間複雜度

與時間複雜度類似，一般也使用大 $O$ 表示法來衡量：一個算法執行隨數據規模增大，而增長的額外空間成本

public static int binarySearchBasic(int[] a, int target) {
    int i = 0, j = a.length - 1;    // 設置指針和初值
    while (i <= j) {                // i~j 範圍內有東西
        int m = (i + j) >>> 1;
        if(target < a[m]) {         // 目標在左邊
            j = m - 1;
        } else if (a[m] < target) { // 目標在右邊
            i = m + 1;
        } else {                    // 找到了
            return m;
        }
    }
    return -1;
}

二分查找性能

下面分析二分查找算法的性能

時間複雜度

最壞情況：$O(\log n)$
最好情況：如果待查找元素恰好在數組中央，只需要循環一次 $O(1)$

空間複雜度

需要常數個指針 $i,j,m$，因此額外佔用的空間是 $O(1)$

1.5 再看二分查找

1) 平衡版

public static int binarySearchBalance(int[] a, int target) {
    int i = 0, j = a.length;
    while (1 < j - i) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m;
        } else {
            i = m;
        }
    }
    return (a[i] == target) ? i : -1;
}

思想：

左閉右開的區間，$i$ 指向的可能是目標，而 $j$ 指向的不是目標
不奢望循環內通過 $m$ 找出目標, 縮小區間直至剩 1 個, 剩下的這個可能就是要找的（通過 $i$）
- $j - i > 1$ 的含義是，在範圍內待比較的元素個數 > 1
改變 $i$ 邊界時，它指向的可能是目標，因此不能 $m+1$
循環內的平均比較次數減少了
時間複雜度 $\Theta(log(n))$

2) Java 版

private static int binarySearch0(long[] a, int fromIndex, int toIndex,
                                     long key) {
    int low = fromIndex;
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        long midVal = a[mid];

        if (midVal < key)
            low = mid + 1;
        else if (midVal > key)
            high = mid - 1;
        else
            return mid; // key found
    }
    return -(low + 1);  // key not found.
}

例如 $[1,3,5,6]$ 要插入 $2$ 那麼就是找到一個位置，這個位置左側元素都比它小
- 等循環結束，若沒找到，low 左側元素肯定都比 target 小，因此 low 即插入點
插入點取負是為了與找到情況區分
-1 是為了把索引 0 位置的插入點與找到的情況進行區分

3) Leftmost 與 Rightmost

有時我們希望返回的是最左側的重複元素，如果用 Basic 二分查找

對於數組 $[1, 2, 3, 4, 4, 5, 6, 7]$，查找元素4，結果是索引3
對於數組 $[1, 2, 4, 4, 4, 5, 6, 7]$，查找元素4，結果也是索引3，並不是最左側的元素

public static int binarySearchLeftmost1(int[] a, int target) {
    int i = 0, j = a.length - 1;
    int candidate = -1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else if (a[m] < target) {
            i = m + 1;
        } else {
            candidate = m; // 記錄候選位置
            j = m - 1;     // 繼續向左
        }
    }
    return candidate;
}

如果希望返回的是最右側元素

public static int binarySearchRightmost1(int[] a, int target) {
    int i = 0, j = a.length - 1;
    int candidate = -1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else if (a[m] < target) {
            i = m + 1;
        } else {
            candidate = m; // 記錄候選位置
            i = m + 1;       // 繼續向右
        }
    }
    return candidate;
}

應用

對於 Leftmost 與 Rightmost，可以返回一個比 -1 更有用的值

Leftmost 改為

public static int binarySearchLeftmost(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target <= a[m]) {
            j = m - 1;
        } else {
            i = m + 1;
        }
    }
    return i; 
}

leftmost 返回值的另一層含義：$\lt target$ 的元素個數
小於等於中間值，都要向左找

Rightmost 改為

public static int binarySearchRightmost(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else {
            i = m + 1;
        }
    }
    return i - 1;
}

大於等於中間值，都要向右找

幾個名詞

file

範圍查詢：

查詢 $x \lt 4$，$0 .. leftmost(4) - 1$
查詢 $x \leq 4$，$0 .. rightmost(4)$
查詢 $4 \lt x$，$rightmost(4) + 1 .. \infty $
查詢 $4 \leq x$， $leftmost(4) .. \infty$
查詢 $4 \leq x \leq 7$，$leftmost(4) .. rightmost(7)$
查詢 $4 \lt x \lt 7$，$rightmost(4)+1 .. leftmost(7)-1$

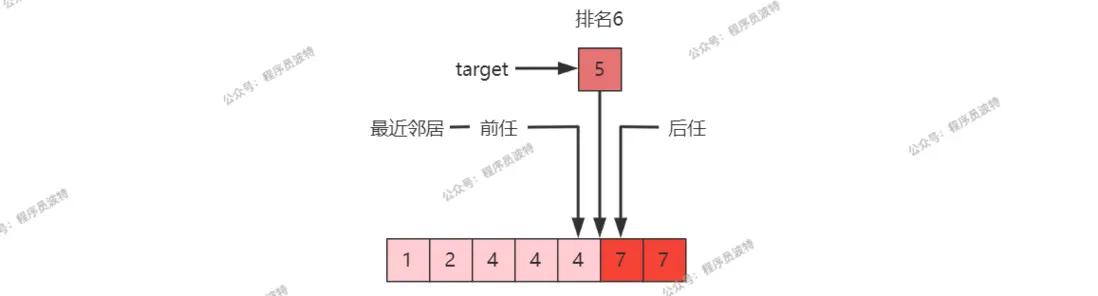
求排名：$leftmost(target) + 1$

$target$ 可以不存在，如：$leftmost(5)+1 = 6$
$target$ 也可以存在，如：$leftmost(4)+1 = 3$

求前任（predecessor）：$leftmost(target) - 1$

$leftmost(3) - 1 = 1$，前任 $a_1 = 2$
$leftmost(4) - 1 = 1$，前任 $a_1 = 2$

求後任（successor）：$rightmost(target)+1$

$rightmost(5) + 1 = 5$，後任 $a_5 = 7$
$rightmost(4) + 1 = 5$，後任 $a_5 = 7$

求最近鄰居：

前任和後任距離更近者

習題

1) 時間複雜度估算

用函數 $f(n)$ 表示算法效率與數據規模的關係，假設每次解決問題需要 1 微秒（$10^{-6}$ 秒），進行估算：

如果 $f(n) = n^2$ 那麼 1 秒能解決多少次問題？1 天呢？
如果 $f(n) = log_2(n)$ 那麼 1 秒能解決多少次問題？1 天呢？
如果 $f(n) = n!$ 那麼 1 秒能解決多少次問題？1 天呢？

參考解答

1秒 $\sqrt{10^6} = 1000$ 次，1 天 $\sqrt{10^6 * 3600 * 24} \approx 293938$ 次
1秒 $2^{1,000,000} $ 次，一天 $2^{86,400,000,000}$
推算如下
- $10! = 3,628,800$ 1秒能解決 $1,000,000$ 次，因此次數為 9 次
- $14!=87,178,291,200$，一天能解決 $86,400,000,000$ 次，因此次數為 13 次

2) 耗時估算

一台機器對200個單詞進行排序花了200秒(使用冒泡排序)，那麼花費800秒，大概可以對多少個單詞進行排序

a. 400

b. 600

c. 800

d. 1600

答案

解釋

冒泡排序時間複雜度是 $O(N^2)$
時間增長 4 倍，而因此能處理的數據量是原來的 $\sqrt{4} = 2$ 倍

3) E01. 二分查找-Leetcode 704

要點：減而治之，可以用遞歸或非遞歸實現

給定一個 n 個元素有序的（升序）整型數組 nums 和一個目標值 target ，寫一個函數搜索 nums 中的 target，如果目標值存在返回下標，否則返回 -1

例如

輸入: nums = [-1,0,3,5,9,12], target = 9
輸出: 4
解釋: 9 出現在 nums 中並且下標為 4
    
輸入: nums = [-1,0,3,5,9,12], target = 2
輸出: -1
解釋: 2 不存在 nums 中因此返回 -1

參考答案：略，可以用講過的任意一種二分求解

4) E02. 搜索插入位置-Leetcode 35

要點：理解誰代表插入位置

給定一個排序數組和一個目標值

在數組中找到目標值，並返回其索引
如果目標值不存在於數組中，返回它將會被按順序插入的位置

例如

輸入: nums = [1,3,5,6], target = 5
輸出: 2

輸入: nums = [1,3,5,6], target = 2
輸出: 1

輸入: nums = [1,3,5,6], target = 7
輸出: 4

參考答案1：用二分查找基礎版代碼改寫，基礎版中，找到返回 m，沒找到 i 代表插入點，因此有

public int searchInsert(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else if (a[m] < target) {
            i = m + 1;
        } else {
            return m;
        }
    }
    return i; // 原始 return -1
}

參考答案2：用二分查找平衡版改寫，平衡版中

如果 target == a[i] 返回 i 表示找到
如果 target < a[i]，例如 target = 2，a[i] = 3，這時就應該在 i 位置插入 2
如果 a[i] < target，例如 a[i] = 3，target = 4，這時就應該在 i+1 位置插入 4

public static int searchInsert(int[] a, int target) {
    int i = 0, j = a.length;
    while (1 < j - i) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m;
        } else {
            i = m;
        }
    }
    return (target <= a[i]) ? i : i + 1;
    // 原始 (target == a[i]) ? i : -1;
}

參考答案3：用 leftmost 版本解，返回值即為插入位置（並能處理元素重複的情況）

public int searchInsert(int[] a, int target) {
    int i = 0, j = a.length - 1;
    while(i <= j) {
        int m = (i + j) >>> 1;
        if(target <= a[m]) {
            j = m - 1;
        } else {
            i = m + 1;
        } 
    }
    return i;
}

5) E03. 搜索開始結束位置-Leetcode 34

給你一個按照非遞減順序排列的整數數組 nums，和一個目標值 target。請你找出給定目標值在數組中的開始位置和結束位置。

如果數組中不存在目標值 target，返回 [-1, -1]。

你必須設計並實現時間複雜度為 O(log n) 的算法解決此問題

例如

輸入：nums = [5,7,7,8,8,10], target = 8
輸出：[3,4]

輸入：nums = [5,7,7,8,8,10], target = 6
輸出：[-1,-1]

輸入：nums = [], target = 0
輸出：[-1,-1]

參考答案

public static int left(int[] a, int target) {
    int i = 0, j = a.length - 1;
    int candidate = -1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else if (a[m] < target) {
            i = m + 1;
        } else {
            candidate = m;
            j = m - 1;
        }
    }
    return candidate;
}

public static int right(int[] a, int target) {
    int i = 0, j = a.length - 1;
    int candidate = -1;
    while (i <= j) {
        int m = (i + j) >>> 1;
        if (target < a[m]) {
            j = m - 1;
        } else if (a[m] < target) {
            i = m + 1;
        } else {
            candidate = m;
            i = m + 1;
        }
    }
    return candidate;
}

public static int[] searchRange(int[] nums, int target) {
    int x = left(nums, target);
    if(x == -1) {
        return new int[] {-1, -1};
    } else {
        return new int[] {x, right(nums, target)};
    }
}