函數遞歸與題目解析——C語言詳情 - c BlackQid 動態日志

1 遞歸是什麼?

遞歸是一種解決問題的方法，在C語言中，遞歸就是函數自己調用自己。

1.1 遞歸的思想

把一個大型複雜問題層層轉化為一個與原問題相似，但規模較小的子問題來求解；直到子問題不能再被拆分，遞歸就結束了。所以遞歸的思考方式就是把大事化小的過程。

遞歸中的遞就是遞推的意思，歸就是迴歸的意思，接下來慢慢來體會。

1.2 遞歸的限制條件

遞歸在書寫的時候，有2個必要條件：

遞歸存在限制條件，當滿足這個限制條件的時候，遞歸便不再繼續。
每次遞歸調用之後越來越接近這個限制條件。

在下面的例子中，我們逐步體會這2個限制條件。

2 遞歸題目解析

2.1 求n的階乘

一個正整數的階乘(factorial)是所有小於及等於該數的正整數的積，並且0的階乘為1。

自然數n的階乘寫作n!。

題目：計算n的階乘(不考慮溢出)，n的階乘就是1~n的數字累積相乘。

2.1.1 分析和代碼實現

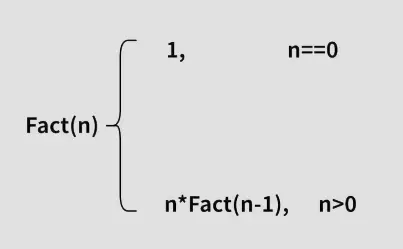
我們知道n的階乘的公式：n! = n * (n一1)!

從這個公式不難看出：如何把一個較大的問題，轉換為一個與原問題相似，但規模較小的問題來求解的。

n的階乘和n-1的階乘是相似的問題，但是規模要少了n。有一種有特殊情況是：當n==0的時候，n的階乘是1，而其餘n的階乘都是可以通過上面的公式計算。

這樣就能寫出n的階乘的遞歸公式:

那我們就可以寫出函數Fact()求n的階乘（遞歸是基於函數的），假設Fact(n)就是求n的階乘，那麼Fact(n-1)就是求n-1的階乘，函數如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>

//遞歸
int Func(int n)
{
    if (n == 0)
        return 1;
    return n * Func(n - 1);
}

//非遞歸
int Func2(int n)
{
    int m = 1;
    for (int i = 1; i <= n; i++)
    {
        m *= i;
    }
    return m;
}

int main()
{
    int n = 5;
    printf("%d\n", Func(n));
    printf("%d\n", Func2(n));
    return 0;
}

2.2 順序打印一個整數的每一位

輸入一個整數m，按照順序打印整數的每一位。

比如：

輸入：1234 輸出：1 2 3 4

輸入：520 輸出：5 2 0

2.2.1 分析和代碼實現

這個題目，放在我們面前，首先想到的是，怎麼得到這個數的每一位呢?

如果n是一位數，n的每一位就是n自己

n是超過1位數的話，就得拆分每一位

1234%10就能得到4,然後1234/10得到123,這就相當於去掉了4

然後繼續對123%10,就得到了3,再除10去掉3,以此類推

不斷的%10和/10操作，直到1234的每一位都得到;

但是這裏有個問題就是得到的數字順序是倒着的

但是我們有了靈感，我們發現其實一個數字的最低位是最容易得到的，通過%10就能得到

那我們假設想寫一個函數Print()來打印n的每一位，如下表示：

如果n是1234，那表示為

Print(1234) //打印1234的每一位

其中1234中的4可以通過%10得到，那麼

Print(1234)就可以拆分為兩步：

Print(1234/10) //打印123的每一位
printf(1234%10) //打印4

完成上述2步，那就完成了1234每一位的打印

那麼Print(123)又可以拆分為Print(123/10) + printf (123%10)

以此類推下去，直到被打印的數字變成一位數的時候，就不需要再拆分，遞歸結束。

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//打印一個數的每一位
void Print(int n)
{
    if (n > 9)
    {
        Print(n / 10);
    }
    printf("%d ", n%10);
}

int main()
{
    int n = 1234;
    Print(n);

    return 0;
}

在這個解題的過程中，我們就是使用了大事化小的思路

把Print(1234)打印1234每一位，拆解為首先Print(123)打印123的每一位，再打印得到的4

把Print(123)打印123每一位，拆解為首先Print(12)打印12的每一位，再打印得到的3

直到Print打印的是一位數，直接打印就行。

2.3 青蛙跳台階問題[1]

一隻青蛙一次可以跳上1級台階，也可以跳上2級。求該青蛙跳上一個n級的台階總共有多少種跳法（先後次序不同算不同的結果）。

2.3.1 分析和代碼實現

我們設定Jump(n)可以計算青蛙跳上一個n級的台階總共有多少種跳法。

假設n = 4，青蛙跳到第4級台階時有兩種跳法，從第3級跳上來或者從第2級跳上來

可以寫作Jump(4) = Jump(3) + Jump(2)

而青蛙跳到第3級台階時也有兩種跳法，從第2級跳上來或者從第1級跳上來

Jump(3) = Jump(2) + Jump(1)

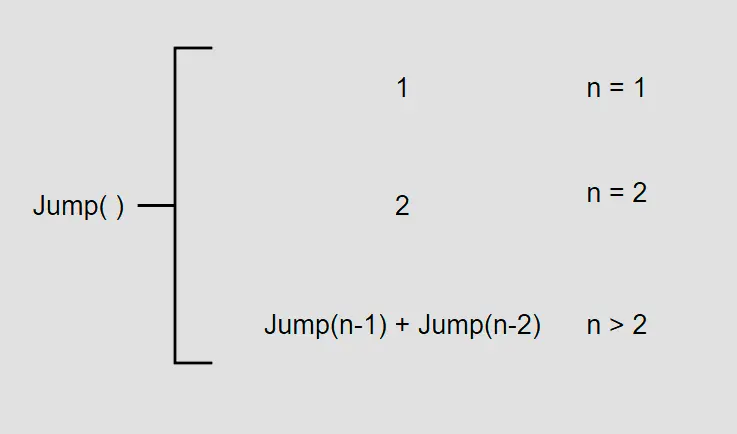
我們知道當台階為1級時，只有1種跳法；為2級時，有2種跳法。

即 Jump(2) = 2；Jump(1) = 1

接下來我們推廣到第n級（n>2）台階時前一次跳的情況。它也有兩種跳法：一是從第n-1級台階起跳，二是從第n-2級台階起跳。這樣一來，我們就可以寫出關於n的遞推公式：

那我們就可以寫出函數Jump()求n級台階的跳法，假設Jump(n)就是到n級台階的跳法，那麼Jump(n-1)就是求到n-1級台階的跳法，Jump(n-2)就是求到n-2級台階的跳法，函數如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>


//青蛙跳台階

int Jump(int x)
{
    if (x == 1)
        return 1;
    else if (x == 2)
        return 2;
    else
        return Jump(x - 1) + Jump(x - 2);
}


int main()
{
    int n = 4;
    int ret = Jump(n);
    printf("%d\n", ret);
    return 0;
}

2.4 計算一個數的每位之和

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//計算一個數的每位之和
int DigitSum(int n)
{
    if (n < 10)
    {
        return n;
    }
    return n%10 + DigitSum(n/10);
}

int main()
{
    int n = 1234;
    printf("%d", DigitSum(n));
    return 0;
}

2.5 計算x的y次冪

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//計算x的y次冪
int MI(int x, int y)
{
    if (y == 0)
        return 1;
    else if (y == 1)
        return x;
    else
        return x * MI(x, y - 1);
}

int main()
{
    int x = 0;
    int y = 0;
    scanf("%d %d", &x, &y);
    int ret = MI(x, y);
    printf("%d\n", ret);
    return 0;
}

2.6 漢諾塔問題[2]

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
//漢諾塔
void Print(char x, char y)
{
    printf("%c->%c ", x, y);
}
void Hanno(int x, char pos1, char pos2, char pos3)
{
    if (x == 1)
        Print(pos1, pos3);
    else
    {
        Hanno(x - 1, pos1, pos3, pos2);
        Print(pos1, pos3);
        Hanno(x - 1, pos2, pos1, pos3);
    }
}

int main()
{
    int n = 3;
    Hanno(n,'A','B','C');
    return 0;
}