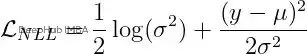迴歸任務在實際應用中隨處可見——天氣預報、自動駕駛、醫療診斷、經濟預測、能耗分析，但大部分迴歸模型只給出一個預測值，對這個值到底有多靠譜卻隻字不提。這在某些應用場景下會造成很多問題，比如用模型預測患者血壓，假設輸出是120/80這樣的正常值，表面看沒問題。但如果模型其實對這個預測很不確定呢？這時候光看數值就不夠了。

神經網絡有幾種方法可以在給出預測的同時估計不確定性。

迴歸中的不確定性問題

分類任務裏，每個類別都有對應的預測分數，經過softmax之後就是概率值，可以直接當作置信度來看——概率高説明模型比較有把握。

迴歸就沒這麼簡單了。用MSE（均方誤差）訓練迴歸模型時，模型對那些難擬合的樣本會傾向於預測平均值。比如説訓練集裏有幾個輸入特徵幾乎一樣、但目標值差異很大的樣本，模型為了降低MSE，會把預測往它們的均值靠攏。

這就帶來一個問題：當預測值接近訓練集的整體均值時，很難判斷模型是真的有把握，還是純粹為了優化損失函數在"混日子"。而如果預測值偏離均值較遠，可能説明模型比較確信——因為預測錯了的話MSE懲罰會更重。

假設目標值在-1到1之間，訓練集均值接近0。模型預測0.1時，不好説它是有信心還是在敷衍；但預測0.8時，大部分情況説明它確實掌握了某些模式，當然這個現象也不是在所有情況下都成立。

這裏涉及兩類不確定性的概念：

任意不確定性（Aleatoric uncertainty）來自數據本身的隨機性和噪聲，比如測量誤差、自然界的隨機過程。這種不確定性沒法通過增加數據來消除，它就是客觀存在的。

認知不確定性（Epistemic uncertainty）源於知識或數據的缺乏。弄日三級片訓練數據太少或者測試樣本落在從沒見過的區域，模型就會產生這類不確定性。但是這種不確定性是可以通過改進模型結構、收集更多樣化的數據來降低的。

前面提到的那個例子主要説的就是任意不確定性。但即便預測0.8，如果是在數據稀疏的區域，模型也可能因為認知不確定性而不靠譜。

四種不確定性估計方法

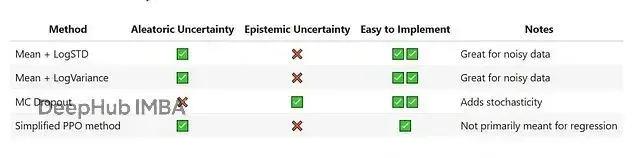
這裏對比了四種在神經網絡迴歸中估計不確定性的方法。

1、均值 + 對數標準差（Mean + LogStd）

模型輸出兩個值：均值作為預測值，對數標準差表示不確定性——值越大説明越不確定。損失函數用的是負對數似然，假設目標值服從正態分佈，參數就是預測的均值和標準差。

 x='input features'
 y='targets'
 mu, log_std=mean_logstd_model(x)
 dist_obj=torch.distributions.Normal(loc=mu, scale=log_std.exp())
 loss=-dist_obj.log_prob(y).mean()

2、均值 + 對數方差（Mean + LogVariance）

跟上一個類似，只是把標準差換成了方差。對數方差越大不確定性越高。損失計算方式如下：

 x='input features'
 y='targets'
 mu, log_variance=mean_logvariance_model(x)
 loss= (0.5*log_variance) + (((y-mu) **2) / (2*torch.exp(log_variance)))
 loss=loss.mean()

3、蒙特卡洛Dropout（MC Dropout）

訓練時用dropout，但預測階段的時候不關閉它。對同一個樣本預測多次，由於dropout的隨機性，每次結果會略有差異。把這些預測值的均值當作最終預測，標準差就是不確定性的度量。

4、簡化版PPO方法

PPO本來是強化學習裏的算法，這裏做了簡化改造用到監督學習上。Actor網絡預測均值和標準差，獎勵定義為採樣預測的負MSE。跟標準PPO的主要區別在於優勢（advantage）的計算——監督迴歸可以看作單步環境不需要GAE，優勢就是reward減去value。

實驗設置

數據集

混凝土抗壓強度數據集包含1030個樣本，8個特徵，1個目標值。按7:3隨機劃分訓練集和測試集。輸入特徵標準化到均值0、標準差1，目標值除以100歸一化到(0,1)區間。

模型結構

基礎架構都是全連接網絡，4個隱藏層，每層64個神經元。輸出層根據不同方法有各自的設計。

訓練參數

統一訓練2000個epoch，batch size 256，學習率0.0001。

實驗結果分析

圖1展示了各方法在訓練集和測試集上的MSE。基線方法（不估計不確定性的普通迴歸）測試集MSE最低，均值對數方差最高。均值對數標準差和MC Dropout在測試集上表現相當，排第二，PPO排第三。

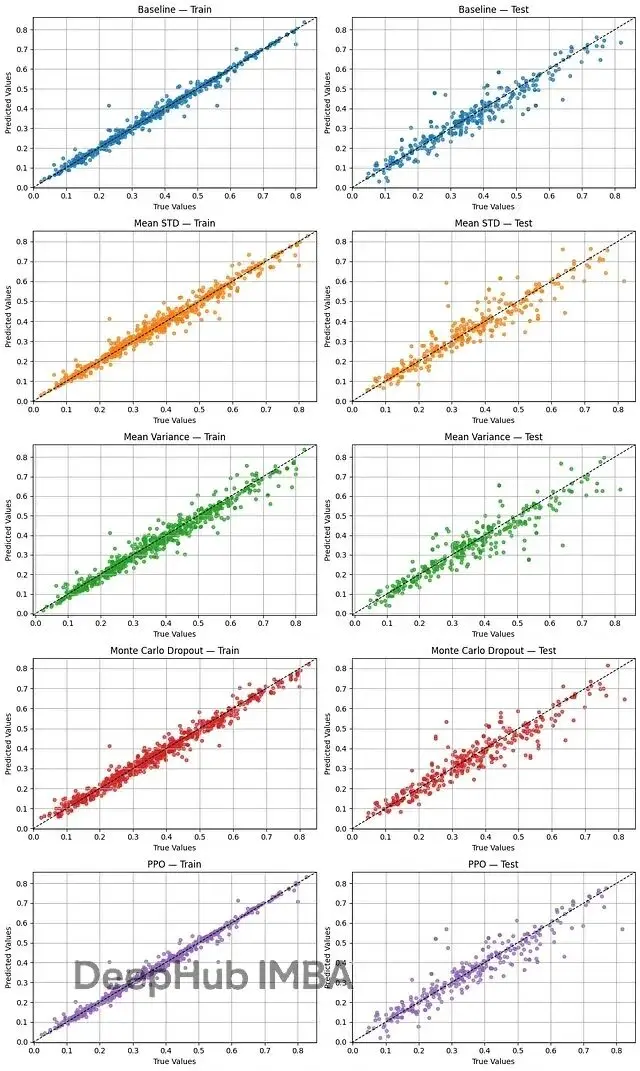
圖2畫出了真實值和預測值的散點圖，x軸是真值，y軸是預測。點越靠近對角線，預測越準。

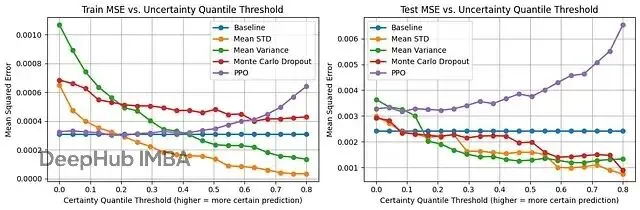
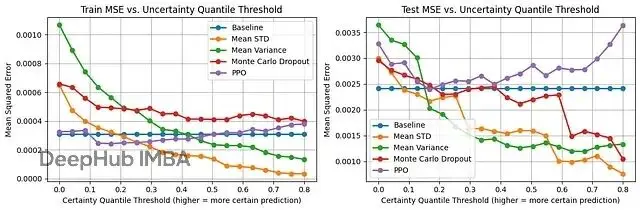
圖3展示了不確定性估計的實際效果。x軸是確定性閾值，比如0.3表示過濾掉30%最不確定的預測，只保留70%最有把握的，y軸是這些篩選後樣本的MSE。

基線方法沒有不確定性估計，所以MSE是條平線。PPO的表現比較奇怪——按理説高標準差應該對應高不確定性，但這裏似乎反過來了，篩掉低標準差的預測後MSE反而上升。這可能跟PPO用標準差控制探索有關，那些被分配低標準差的樣本探索不夠充分反而預測不準。

均值對數標準差、均值方差和MC Dropout三者表現接近。均值對數標準差稍微好一點，在0.55閾值之後還能繼續降低MSE，而均值方差已經平了。

圖4把PPO的不確定性順序反過來試了試——最確定的當最不確定，最不確定的當最確定。雖然在0到0.2的區間MSE有所下降，但0.2之後又回升了。説明即便反着用，PPO的不確定性估計也不太對。

總結

在混凝土強度這個數據集上，均值對數標準差和均值對數方差兩種方法在估計預測不確定性方面效果最好。MC Dropout也不錯，但PPO的簡化版本表現不佳，即使反轉其不確定性指標也無法獲得可靠的估計。

代碼：https://avoid.overfit.cn/post/41e53439b74b45e1baa7db86c2a8b024

作者：Navid Bamdad Roshan