文章內容整理自【博學谷狂野架構師】
索引(index)是幫助MySQL高效獲取數據的數據結構(有序)。在數據之外,數據庫系統還維護着滿足 特定查找算法的數據結構,這些數據結構以某種方式引用(指向)數據, 這樣就可以在這些數據結構 上實現高級查找算法,這種數據結構就是索引。

優缺點:
優點:
- 提高數據檢索效率,降低數據庫的IO成本
- 通過索引列對數據進行排序,降低數據排序的成本,降低CPU的消耗
缺點:
- 索引列也是要佔用空間的
- 索引大大提高了查詢效率,但降低了更新的速度,比如 INSERT、UPDATE、DELETE
索引結構
| 索引結構 | 描述 |
|---|---|
| B+Tree | 最常見的索引類型,大部分引擎都支持B+樹索引 |
| Hash | 底層數據結構是用哈希表實現,只有精確匹配索引列的查詢才有效,不支持範圍查詢 |
| R-Tree(空間索引) | 空間索引是 MyISAM 引擎的一個特殊索引類型,主要用於地理空間數據類型,通常使用較少 |
| Full-Text(全文索引) | 是一種通過建立倒排索引,快速匹配文檔的方式,類似於 Lucene, Solr, ES |
- 上述是MySQL中所支持的所有的索引結構,接下來,我們再來看看不同的存儲引擎對於索引結構的支持 情況。
| 索引 | InnoDB | MyISAM | Memory |
|---|---|---|---|
| B+Tree索引 | 支持 | 支持 | 支持 |
| Hash索引 | 不支持 | 不支持 | 支持 |
| R-Tree索引 | 不支持 | 支持 | 不支持 |
| Full-text | 5.6版本之後支持 | 支持 | 不支持 |
注意: 我們平常所説的索引,如果沒有特別指明,都是指B+樹結構組織的索引。
二叉樹
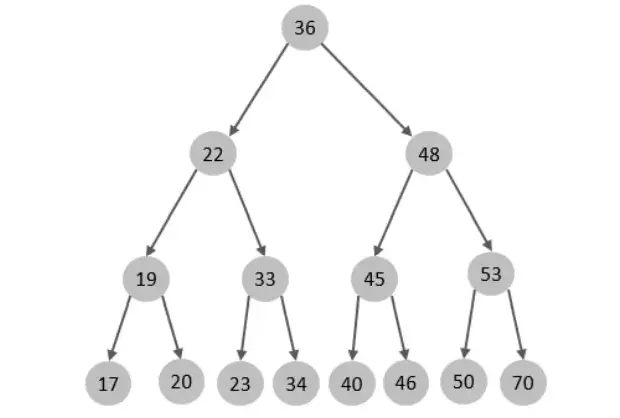
假如説MySQL的索引結構採用二叉樹的數據結構,比較理想的結構如下:
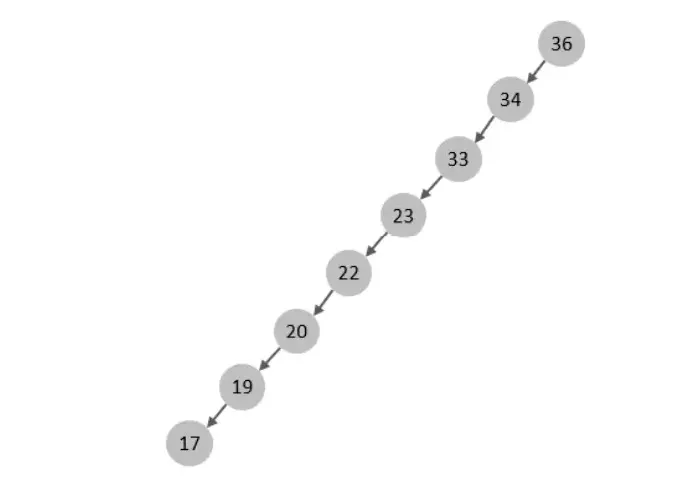
如果主鍵是順序插入的,則會形成一個單向鏈表,結構如下:
所以,如果選擇二叉樹作為索引結構,會存在以下缺點:
- 順序插入時,會形成一個鏈表,查詢性能大大降低。
- 大數據量情況下,層級較深,檢索速度慢。
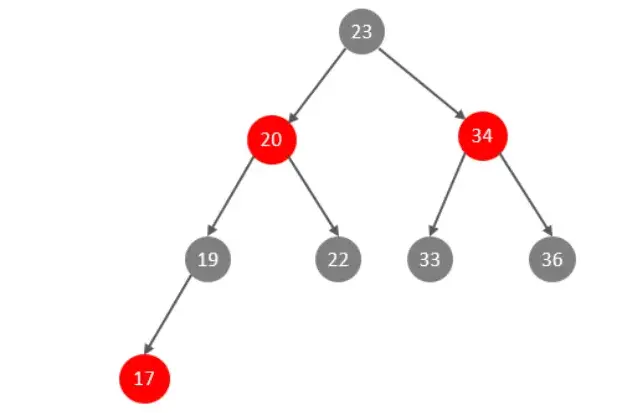
此時大家可能會想到,我們可以選擇紅黑樹,紅黑樹是一顆自平衡二叉樹,那這樣即使是順序插入數據,最終形成的數據結構也是一顆平衡的二叉樹,結構如下:
但是,即使如此,由於紅黑樹也是一顆二叉樹,所以也會存在一個缺點:
- 大數據量情況下,層級較深,檢索速度慢。
所以,在MySQL的索引結構中,並沒有選擇二叉樹或者紅黑樹,而選擇的是B+Tree,那麼什麼是B+Tree呢?在詳解B+Tree之前,先來介紹一個B-Tree。
B-Tree
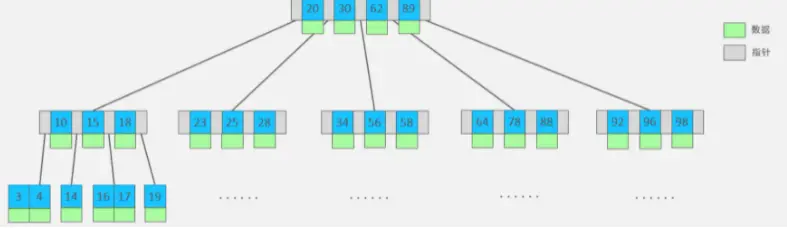
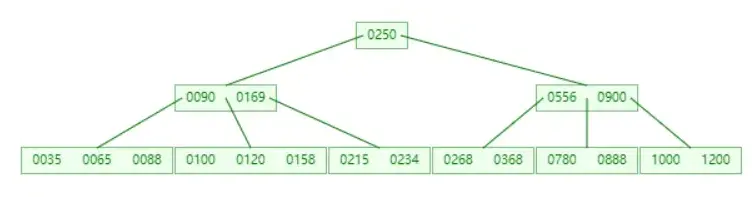
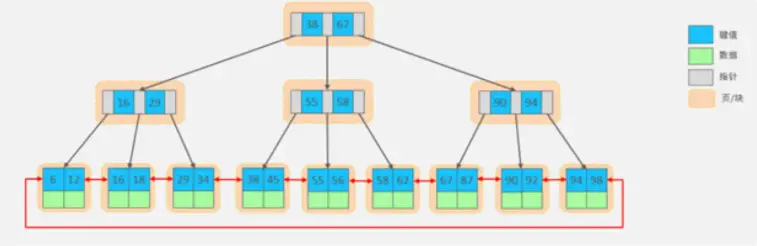
B-Tree,B樹是一種多路衡查找樹,相對於二叉樹,B樹每個節點可以有多個分支,即多叉。以一顆最大度數(max-degree)為5(5階)的b-tree為例,那這個B樹每個節點最多存儲4個key,5個指針:
樹的度數指的是一個節點的子節點個數。
我們可以通過一個數據結構可視化的網站來簡單演示一下。B-Tree Visualization (usfca.edu)(opens new window)
插入一組數據: 100 65 169 368 900 556 780 35 215 1200 234 888 158 90 1000 88 120 268 250 。然後觀察一些數據插入過程中,節點的變化情況。
特點:
- 5階的B樹,每一個節點最多存儲4個key,對應5個指針。
- 一旦節點存儲的key數量到達5,就會裂變,中間元素向上分裂。
- 在B樹中,非葉子節點和葉子節點都會存放數據。
B+Tree
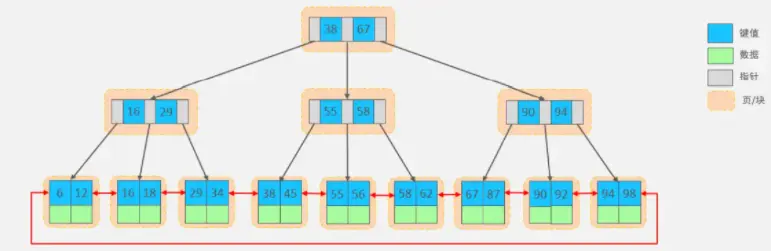
B+Tree是B-Tree的變種,我們以一顆最大度數(max-degree)為4(4階)的b+tree為例,來看一下其結構示意圖:
我們可以看到,兩部分:
- 綠色框框起來的部分,是索引部分,僅僅起到索引數據的作用,不存儲數據。
- 紅色框框起來的部分,是數據存儲部分,在其葉子節點中要存儲具體的數據。
我們可以通過一個數據結構可視化的網站來簡單演示一下。B+ Tree Visualization (usfca.edu)(opens new window)

插入一組數據: 100 65 169 368 900 556 780 35 215 1200 234 888 158 90 1000 88 120 268 250 。然後觀察一些數據插入過程中,節點的變化情況。
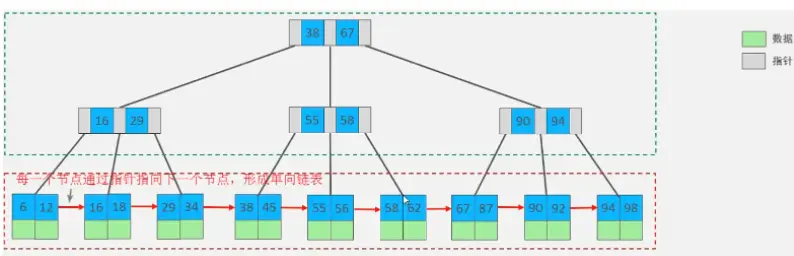
最終我們看到,B+Tree 與 B-Tree相比,主要有以下三點區別:
- 所有的數據都會出現在葉子節點。
- 葉子節點形成一個單向鏈表。
- 非葉子節點僅僅起到索引數據作用,具體的數據都是在葉子節點存放的。
上述我們所看到的結構是標準的B+Tree的數據結構,接下來,我們再來看看MySQL中優化之後的B+Tree。
MySQL索引數據結構對經典的B+Tree進行了優化。在原B+Tree的基礎上,增加一個指向相鄰葉子節點的鏈表指針,就形成了帶有順序指針的B+Tree,提高區間訪問的性能,利於排序。
Hash
MySQL中除了支持B+Tree索引,還支持一種索引類型---Hash索引。
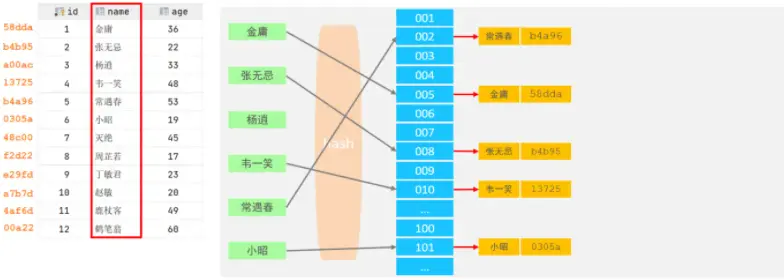
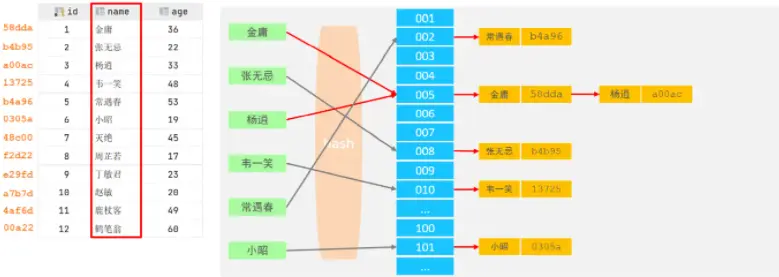
- 結構
哈希索引就是採用一定的hash算法,將鍵值換算成新的hash值,映射到對應的槽位上,然後存儲在hash表中。
如果兩個(或多個)鍵值,映射到一個相同的槽位上,他們就產生了hash衝突(也稱為hash碰撞),可以通過鏈表來解決。
- 特點
- Hash索引只能用於對等比較(=,in),不支持範圍查詢(between,>,< ,...)
- 無法利用索引完成排序操作
- 查詢效率高,通常(不存在hash衝突的情況)只需要一次檢索就可以了,效率通常要高於B+tree索引
- 存儲引擎支持
在MySQL中,支持hash索引的是Memory存儲引擎。 而InnoDB中具有自適應hash功能,hash索引是 InnoDB存儲引擎根據B+Tree索引在指定條件下自動構建的。
思考題: 為什麼InnoDB存儲引擎選擇使用B+tree索引結構?
- 相對於二叉樹,層級更少,搜索效率高;
- 對於B-tree,無論是葉子節點還是非葉子節點,都會保存數據,這樣導致一頁中存儲的鍵值減少,指針跟着減少,要同樣保存大量數據,只能增加樹的高度,導致性能降低;
- 相對Hash索引,B+tree支持範圍匹配及排序操作;
索引的分類
在MySQL數據庫,將索引的具體類型主要分為以下幾類:主鍵索引、唯一索引、常規索引、全文索引。
| 分類 | 含義 | 特點 | 關鍵字 |
|---|---|---|---|
| 主鍵索引 | 針對於表中主鍵創建的索引 | 默認自動創建,只能有一個 | PRIMARY |
| 唯一索引 | 避免同一個表中某數據列中的值重複 | 可以有多個 | UNIQUE |
| 常規索引 | 快速定位特定數據 | 可以有多個 | |
| 全文索引 | 全文索引查找的是文本中的關鍵詞,而不是比較索引中的值 | 可以有多個 | FULLTEXT |
在 InnoDB 存儲引擎中,根據索引的存儲形式,又可以分為以下兩種:
| 分類 | 含義 | 特點 |
|---|---|---|
| 聚集索引(Clustered Index) | 將數據存儲與索引放一塊,索引結構的葉子節點保存了行數據 | 必須有,而且只有一個 |
| 二級索引(Secondary Index) | 將數據與索引分開存儲,索引結構的葉子節點關聯的是對應的主鍵 | 可以存在多個 |
聚集索引選取規則:
- 如果存在主鍵,主鍵索引就是聚集索引
- 如果不存在主鍵,將使用第一個唯一(UNIQUE)索引作為聚集索引。
- 如果表沒有主鍵,或沒有合適的唯一索引,則InnoDB會自動生成一個rowid作為隱藏的聚集索 引。
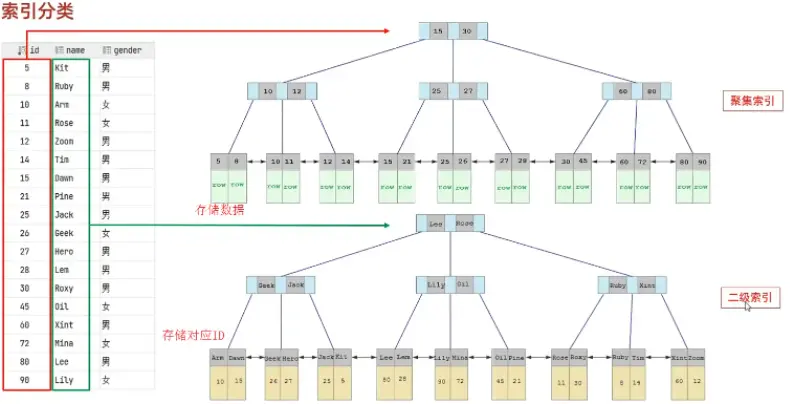
聚集索引和二級索引的具體結構如下:
演示圖:
- 聚集索引的葉子節點下掛的是這一行的數據 。
- 二級索引的葉子節點下掛的是該字段值對應的主鍵值。
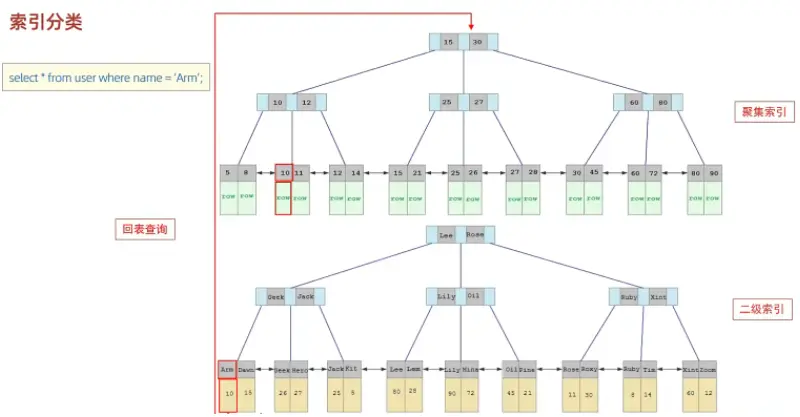
接下來,我們來分析一下,當我們執行如下的SQL語句時,具體的查找過程是什麼樣子的。
具體過程如下:
- 由於是根據name字段進行查詢,所以先根據name='Arm'到name字段的二級索引中進行匹配查 找。但是在二級索引中只能查找到 Arm 對應的主鍵值 10。
- 由於查詢返回的數據是*,所以此時,還需要根據主鍵值10,到聚集索引中查找10對應的記錄,最 終找到10對應的行row。
- 最終拿到這一行的數據,直接返回即可。
回表查詢: 這種先到二級索引中查找數據,找到主鍵值,然後再到聚集索引中根據主鍵值,獲取 數據的方式,就稱之為回表查詢。
思考題:
以下兩條SQL語句,那個執行效率高? 為什麼?
A. select * from user where id = 10 ;
B. select * from user where name = 'Arm' ;
備註: id為主鍵,name字段創建的有索引;
解答:
- A 語句的執行性能要高於B 語句。
- 因為A語句直接走聚集索引,直接返回數據。 而B語句需要先查詢name字段的二級索引,然後再查詢聚集索引,也就是需要進行回表查詢。
思考題:
- InnoDB主鍵索引的B+tree高度為多高呢?
答:假設一行數據大小為1k,一頁中可以存儲16行這樣的數據。InnoDB 的指針佔用6個字節的空間,主鍵假設為bigint,佔用字節數為8. 可得公式:
n * 8 + (n + 1) * 6 = 16 * 1024,其中 8 表示 bigint 佔用的字節數,n 表示當前節點存儲的key的數量,(n + 1) 表示指針數量(比key多一個)。算出n約為1170。如果樹的高度為2,那麼他能存儲的數據量大概為:
1171 * 16 = 18736; 如果樹的高度為3,那麼他能存儲的數據量大概為:1171 * 1171 * 16 = 21939856。另外,如果有成千上萬的數據,那麼就要考慮分表,涉及運維篇知識
如果本文對您有幫助,歡迎
關注和點贊`,您的支持是我堅持創作的動力。轉載請註明出處!