動態

詳情 返回 返回

【工程應用十】 基於Hessian矩陣的Frangi濾波算法 == 血管圖像增強 == Matlab中fibermetric函數的自我實現、加速和優化。 - 動態 詳情

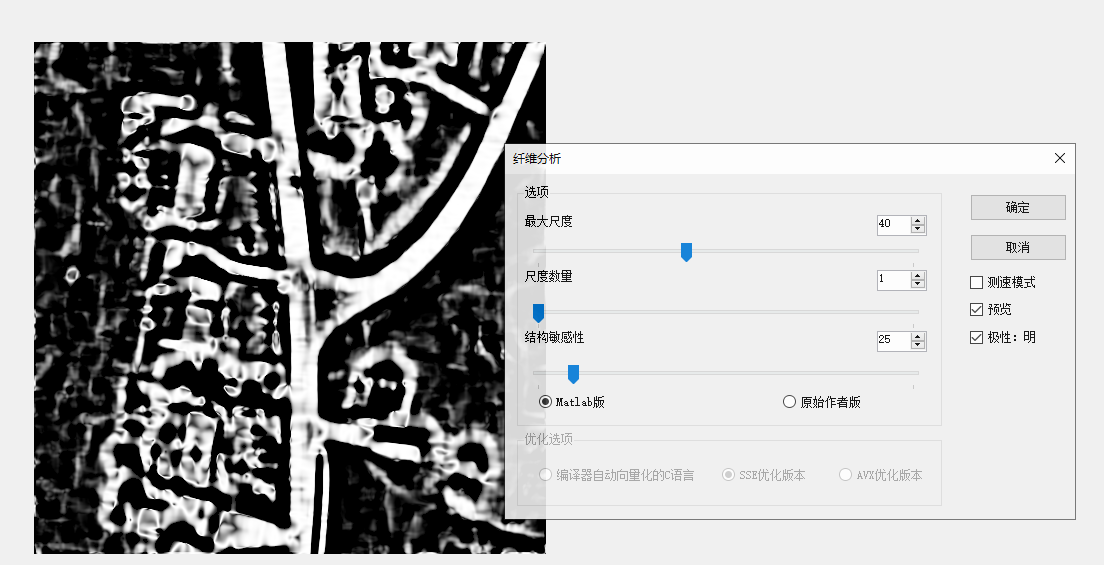
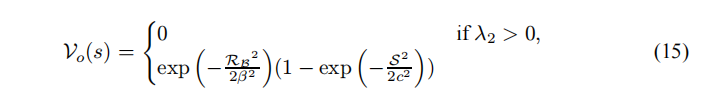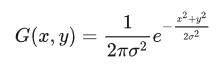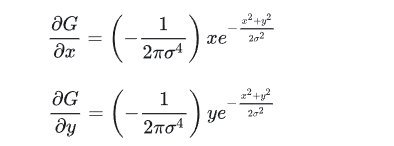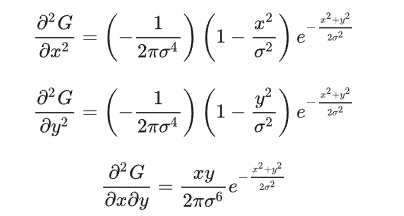　　前幾天在翻一翻matlab中的幫助文檔，無意中發現一個叫fibermetric的圖像處理函數，感覺有點意思，可以增強或者説突出一些類似於管狀的對象，後面看了下算法的幫助文檔，在百度上找了找，原來這也是一種比較經典的增強算法。

　　核心的論文是《Multiscale vessel enhancement filtering》，可以從這裏下載得到：https://www.researchgate.net/publication/2388170_Multiscale_Vessel_Enhancement_Filtering；

　　至於論文的思想，除了直接看原始論文，我也還參考了一下幾篇文章：

　　https://ww2.mathworks.cn/matlabcentral/fileexchange/24409-hessian-based-frangi-vesselness-filter Hessian based Frangi Vesselness filter   原始作者的matlab實現
　　https://github.com/BoguslawObara/vesselness2d 　　　　 　　 　   2d multiscale vessel enhancement filtering
 　  https://www.cnblogs.com/jsxyhelu/p/18157603 　　　　 　　 　　   Hessian矩陣以及在血管增強中的應用——OpenCV實現【2024年更新】
      https://blog.csdn.net/piaoxuezhong/article/details/78428785　　　　眼底圖像血管增強與分割--（5）基於Hessian矩陣的Frangi濾波算法
　  https://blog.csdn.net/lwzkiller/article/details/55050275 　　　　 　　 Hessian矩陣以及在圖像中的應用
 　 https://zhuanlan.zhihu.com/p/127951058 　　　　　　　　　　　　 Multiscale Vessel Enhancement Filtering(多尺度血管增強濾波，基本是對原英文的翻譯）

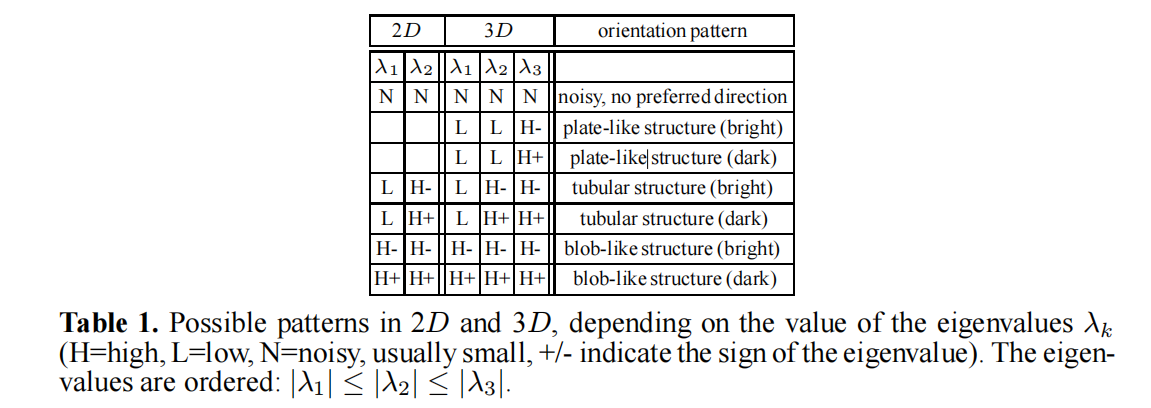
　　但是説實在的我沒有看明白原理，懵懵懂懂的，反正大概就是知道通過判斷Hessian矩陣的兩個特徵值之間的某些關係可以確定某個位置是否屬於血管或者説管狀結構，我覺得呢大概看懂論文裏這個表可能就比較好了：

　　我們重點關注2D的情況。

　　表中Lambda1和Lambda2分別為某個尺度下的Hessian矩陣的特徵值，並且是|Lambda1| < |Lambda2|，對於管狀對象，一般是|Lambda1| << |Lambda2|，其中 <<表示遠遠小於，另外呢，一個先驗就是在血管圖像中背景部分的像素其Hessian矩陣的特徵值一般都比較小，因此，基於這兩個特徵呢，構造了一下兩個中間變量來衡量一個位置的像素是屬於血管還是背景：

                      　　　　

　  　　　　

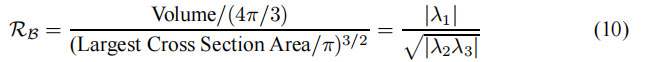
　　對於2D圖像，RB可以簡化為  RB = |Lambda1| / |Lambda2|，而S則即為   S = sqrt(Lambda1^2 + Lambda2^2)；

　　利用這兩個中間變量，然後構架了下式作為某個像素的輸出響應：

　　　　　　

　　其中Beta和C是一些可調節參數，Beta默認可設置為0.5。C後面再説。　　

　　注意觀察，上面公式的下半部分是兩個指數函數的乘積，而指數函數內部的參數必然是負值（2個平方數相除在求負），這個指數函數範圍的有效值為【0,1】，後面部分的1-exp(//)的範圍也必然是【0,1】。 因此2項的乘積必然也是在【0,1】之間。

                           

 　　第一個指數項中，如果RB值越小，則指數值越大，第二個項目中，如果S值越大，則指數值越大， 這恰好正確的反映了前面所説血管區域的特徵。 

　　對於某一個尺度下的響應使用上述公式，而為了獲得更為理想的效果，可以使用連續的多個尺度進行計算，然後取每個尺度下的最大值作為最終的響應值。

　　具體到實現代碼，我們首先參考了論文作者自己的代碼，這個可在https://ww2.mathworks.cn/matlabcentral/fileexchange/24409-hessian-based-frangi-vesselness-filter Hessian based Frangi Vesselness filter下載。

　　我們貼一下這個代碼的主要函數：

sigmas=options.FrangiScaleRange(1):options.FrangiScaleRatio:options.FrangiScaleRange(2);
sigmas = sort(sigmas, 'ascend');
beta  = 2*options.FrangiBetaOne^2;
c     = 2*options.FrangiBetaTwo^2;
% Make matrices to store all filterd images
ALLfiltered=zeros([size(I) length(sigmas)]);
ALLangles=zeros([size(I) length(sigmas)]);
% Frangi filter for all sigmas
for i = 1:length(sigmas),% Make 2D hessian
    [Dxx,Dxy,Dyy] = Hessian2D(I,sigmas(i));
    % Correct for scale
    Dxx = (sigmas(i)^2)*Dxx;
    Dxy = (sigmas(i)^2)*Dxy;
    Dyy = (sigmas(i)^2)*Dyy;
    % Calculate (abs sorted) eigenvalues and vectors
    [Lambda2,Lambda1,Ix,Iy]=eig2image(Dxx,Dxy,Dyy);
    % Compute the direction of the minor eigenvector
    angles = atan2(Ix,Iy);
    % Compute some similarity measures
    Lambda1(Lambda1==0) = eps;
    Rb = (Lambda2./Lambda1).^2;
    S2 = Lambda1.^2 + Lambda2.^2;
    % Compute the output image
    Ifiltered = exp(-Rb/beta) .*(ones(size(I))-exp(-S2/c));
    
    % see pp. 45
    if(options.BlackWhite)
        Ifiltered(Lambda1<0)=0;
    else
        Ifiltered(Lambda1>0)=0;
    end
    % store the results in 3D matrices
    ALLfiltered(:,:,i) = Ifiltered;
    ALLangles(:,:,i) = angles;
end

　　其中Hessian2D的主要代碼如下：

function [Dxx,Dxy,Dyy] = Hessian2D(I,Sigma)
if nargin < 2, Sigma = 1; end
% Make kernel coordinates
[X,Y]   = ndgrid(-round(3*Sigma):round(3*Sigma));
% Build the gaussian 2nd derivatives filters
DGaussxx = 1/(2*pi*Sigma^4) * (X.^2/Sigma^2 - 1) .* exp(-(X.^2 + Y.^2)/(2*Sigma^2));
DGaussxy = 1/(2*pi*Sigma^6) * (X .* Y)           .* exp(-(X.^2 + Y.^2)/(2*Sigma^2));
DGaussyy = DGaussxx';
Dxx = imfilter(I,DGaussxx,'conv');
Dxy = imfilter(I,DGaussxy,'conv');
Dyy = imfilter(I,DGaussyy,'conv');
　　eig2image的主要代碼為：
function [Lambda1,Lambda2,Ix,Iy]=eig2image(Dxx,Dxy,Dyy)
% | Dxx  Dxy |
% |          |
% | Dxy  Dyy |
% Compute the eigenvectors of J, v1 and v2
tmp = sqrt((Dxx - Dyy).^2 + 4*Dxy.^2);
v2x = 2*Dxy; v2y = Dyy - Dxx + tmp;
% Normalize
mag = sqrt(v2x.^2 + v2y.^2); i = (mag ~= 0);
v2x(i) = v2x(i)./mag(i);
v2y(i) = v2y(i)./mag(i);
% The eigenvectors are orthogonal
v1x = -v2y; 
v1y = v2x;
% Compute the eigenvalues
mu1 = 0.5*(Dxx + Dyy + tmp);
mu2 = 0.5*(Dxx + Dyy - tmp);
% Sort eigen values by absolute value abs(Lambda1)<abs(Lambda2)
check=abs(mu1)>abs(mu2);
Lambda1=mu1; Lambda1(check)=mu2(check);
Lambda2=mu2; Lambda2(check)=mu1(check);
Ix=v1x; Ix(check)=v2x(check);
Iy=v1y; Iy(check)=v2y(check);

　　其實不是很複雜，拋開多個尺度取最大值部分，對於單個尺度的結果的計算，主要是以下幾個部分：

　　1、某個尺度下的圖像的二級導數（fxx,fyy以及fxy）.

　　2、由這些導數構成了圖像的Hessian矩陣，求解這個矩陣的特徵值。

　　3、根據特徵值按照前面所描述的公式計算響應值。

　　這裏所謂某個尺度下圖像，就是對原始圖像進行該尺度的高斯模糊後得到的圖像，在所有的可搜索的博文或者代碼中，我們都看到了大家都是按照論文作者提供的matlab代碼的方式，直接根據高斯模糊卷積核的公式，先求出其3種二級偏導數的理論計算公式，然後在根據公式取求取卷積的結果，直接得到二級偏導數，即如下過程：

　　對於2維的高斯模糊，其卷積核為：

　　　　　　　

 　　其一階偏導數為：

　　　　

 　　二階偏導數為：　　　　

　　　　

 　　在上述Hessian2D的matlab代碼中，我們可以找到和這個二級導數對應的離散計算表達式，注意一般高斯相關的計算，因為在3*Sigma範圍外，其權重基本已經衰減到了99%以外了，因此，一般只需要計算3*Sigma半徑內的卷積，如下面的曲面所示：

　         　

　　Hessian2D中的imfilter函數即為實現該卷積的過程。

　　至於Hessian2D的特徵值的計算，因為有固定的計算公式，直接算就可以了，這個沒有什麼好説的。

　　後續響應值的計算，也就是按步就班的來。也沒有什麼可談的。

　　前幾天我也一直按照這個思路來編碼實現效果，那麼做完後呢，確實有結果，不過和matlab的fibermetric相比呢，結果總是有一些區別，而且速度也有較大的差異。我就一直在想，為什麼計算某個尺度下二級導數，一定要直接從那個高斯函數求導後做卷積呢，不能先計算出高斯模糊後的結果後，然後在利用這個結果直接求離散化的二階導數嗎。

　　幸好matlab是個相對不封閉的工具，我們在matlab的窗口中輸入 edit fibermetric，後可以看到他的具體實現，相關代碼如下（做了精簡）：

% Output can be double or single
B = zeros(size(V),'like',V);
numel(thickness)
for id = 1:numel(thickness)
    sigma = thickness(id)/6;
    if (ismatrix(V))
        Ig = imgaussfilt(V, sigma, 'FilterSize', 2*ceil(3*sigma)+1);
    elseif (ndims(V)==3)
        Ig = imgaussfilt3(V,sigma, 'FilterSize', 2*ceil(3*sigma)+1);
    end
    out = images.internal.builtins.fibermetric(Ig, c, isBright, sigma);    
    B = max(B,out);
end

　　代碼不多，但是給出的信息量還是蠻大的，第一輸入參數的thickness和卷積核的參數關係有了對應，即 :

　　　　sigma = thickness(id)/6;

　　為什麼是除以6，我想和剛才那個3*Sigma裏的3應該精密相關吧。

　　第二，可以明顯的看到他是先對原始圖像進行了高斯模糊的，然後在調用一個內部的函數builtins.fibermetric對這個模糊後的圖像進行處理的。由於matlab裏buildins函數是不可以看到源代碼的，所以其具體的進一步實現我們無從得知。但是，這無疑和原始論文作者提供的思路是不一樣，而和我剛才的懷疑則高度一致。於是我按照我自己的想法寫了個過程，其中模糊使用如下方式：

unsigned char* Blur = (unsigned char*)malloc(Height * Stride * sizeof(unsigned char));
IM_GaussBlur_SSE(Src, Blur, Width, Height, Stride, Sigma);

　　得到的結果趨勢和matlab的結果基本一致，但是細節上有很多噪點和干擾。

　　開始的時候我一直認為是這樣做不行，但是看到matlab的實現，我又可以肯定是沒有問題的。因此一直耽擱咋這裏。

　　後面某一刻，我就在想，因為高斯模糊或者或其他的模糊，都會把圖像的細節減少，把尖鋭的地方磨平，因此，模糊的Sigma越大，在離散化計算梯度的時候，如果使用字節版本的模糊呢，由於現相關領域內的像素差異實際上很小了（由浮點數據裁剪到字節數據時丟失了很多信息），因此，就會出現較大的誤差，導致趨勢對，而結果不夠完美。

　　因此，後續我把這個模糊改為浮點版本的模糊，結果就非常的完美了。

　　這裏還有個細節，關於圖像的二階離散的梯度的計算，我們在百度上能搜到的結果是這樣的：   

                       

　　對於fxx,fyy我覺得還是比較合理的，而對於fxy這個結果明顯不太對稱和合理，總感覺有點問題。

　　這個問題的解惑呢，也還是要看機遇，在繼續翻matlab的函數時，我又發現他還有一個maxhessiannorm函數，並且他和fibermetric是精密相關，通過edit maxhessiannorm發現這個函數是完全分享代碼的，其核心代碼如下：

sigma = thickness/6;
[Gxx, Gyy, Gxy]     = images.internal.hessian2D(I, sigma);
[eigVal1, eigVal2]  = images.internal.find2DEigenValues(Gxx, Gyy, Gxy);
absEigVal1 = abs(eigVal1);
absEigVal2 = abs(eigVal2);
maxHessianNorm = max([max(absEigVal1(:)), max(absEigVal2)]);
C = maxHessianNorm;

　　他的作用是獲取最大的Hessian矩陣的特徵值，而且和fibermetric的過程是對應的。

　　我們看這裏的images.internal.hessian2D，還好這個internal是可以看到代碼的。

Ig = imgaussfilt(I, sigma, 'FilterSize', 2*ceil(3*sigma)+1);
[Gx, Gy]   = imgradientxy(Ig, 'central');
[Gxx, Gxy] = imgradientxy(Gx, 'central');
[ ~ , Gyy] = imgradientxy(Gy, 'central');

Gxx = (sigma^2)*Gxx;
Gyy = (sigma^2)*Gyy;
Gxy = (sigma^2)*Gxy;

　　第一行和fibermetric函數是一模一樣的，而後續的三行就是計算二階梯度，在去看imgradientxy的相關注釋，有下面的語句

 'central'               : Central difference gradient dI/dx = (I(x+1)- I(x-1))/ 2

　　這樣，我們一步一步的做個推導，具體如下：

 　　簡單來説，對於如下的一箇中線點像素 P12，

　　　　　　

 　　其二級偏導數分別為：

           //    求該尺度下圖像的二階梯度
            float Dxx = (P14 + P10 - P12 - P12) * 0.25f;
            float Dyy = (P22 + P2 - P12 - P12) * 0.25f;
            float Dxy = (P18 + P6 - P16 - P8) * 0.25f;

　　這個時候在去看Dxy則是完全對稱的了。

　　同時，這個地方還給我解惑了另外一個問題，即在fibermetric的代碼中，還有這樣一句話

 　　　　out = images.internal.builtins.fibermetric(Ig, c, isBright, sigma); 

　按理説，前面高斯模糊需要這個Sigma是無可厚非的，那後面這裏這個函數怎麼還需要傳遞sigma呢，一直不理解，後面看看這個images.internal.hessian2D就明白了，原來是要在這裏用sigma方法放大。
　　　　　　Gxx = (sigma^2)*Gxx;
　　　　　　Gyy = (sigma^2)*Gyy;
　　　　　　Gxy = (sigma^2)*Gxy;
　　最後，在matlab的函數裏，還有一個StructureSensitivity參數，這個我測試了半天，我認為他就是公式中的c變量，這裏有一個很好的理由支撐他， 因為在maxhessiannorm的解釋文檔中，有如下內容：
　　% C = maxhessiannorm(I) calculates the maximum of Frobenius norm of the
　　% hessian of intensity image I. As this function is used in the context
　　% of fibermetric, default thickness of 4 is used to find the hessian and
　　% returns the obtained value as C.
　　
　　第一，這裏直接用的字母C作為返回值，這個是一種遙相呼應，第二，這個函數計算的是特徵值的最大值，和前面的公式變量S精密相關，而S又和C在計算時綁定在一起，因此，他應該就是C的一個外在表現。
　　至此，大部分的工作都已經完成了，而通過這樣的改動，我所實現的結果基本和maltab的完全一致，並且速度方面有高斯模糊有快速的算法，因此算法的執行速度和參數基本無關了。而傳統的那種卷積實現，當尺度較大時，必然會影響速度。 
　　
　　使用相同的圖做測試，500*500的，單尺度時matlab大概需要15ms， 我實現的版本大概在3ms，還是有相當大的提高的。 
 
　　   
　　　　　　　　　　　　　　matlab測試圖　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Thickness等於7時的結果圖

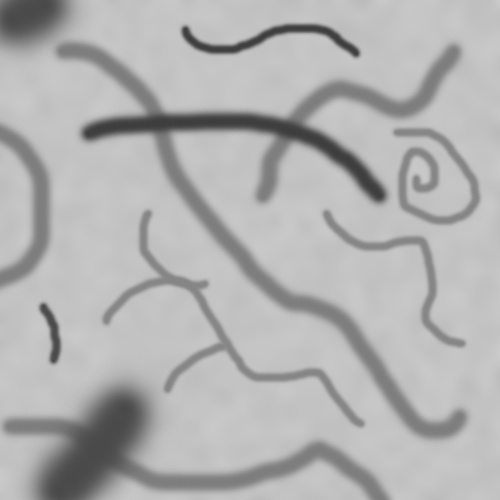
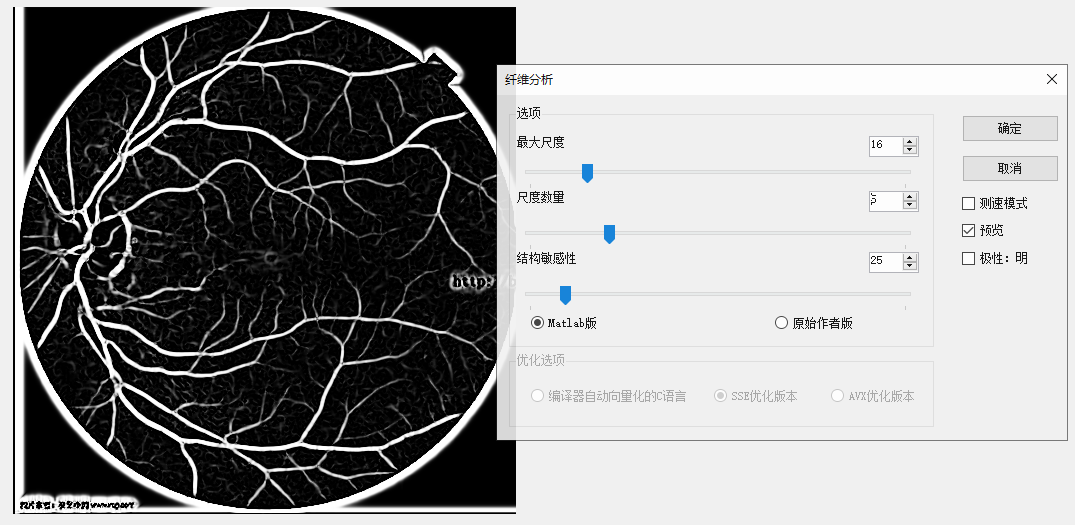
　　那一副醫學圖像做測試，效果確實不錯：

    

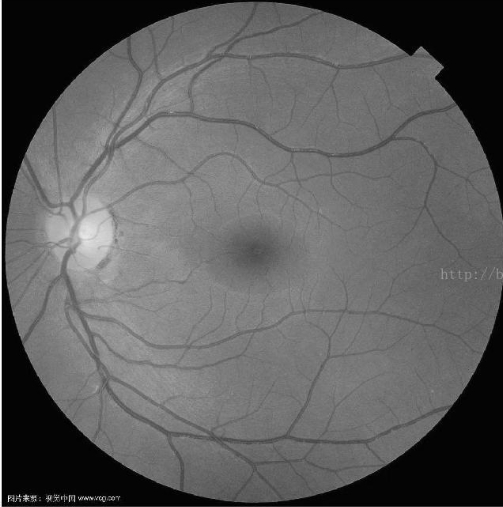
 　　　　　　　　　　原圖　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　尺度數量為5，最大尺度為16的結果 

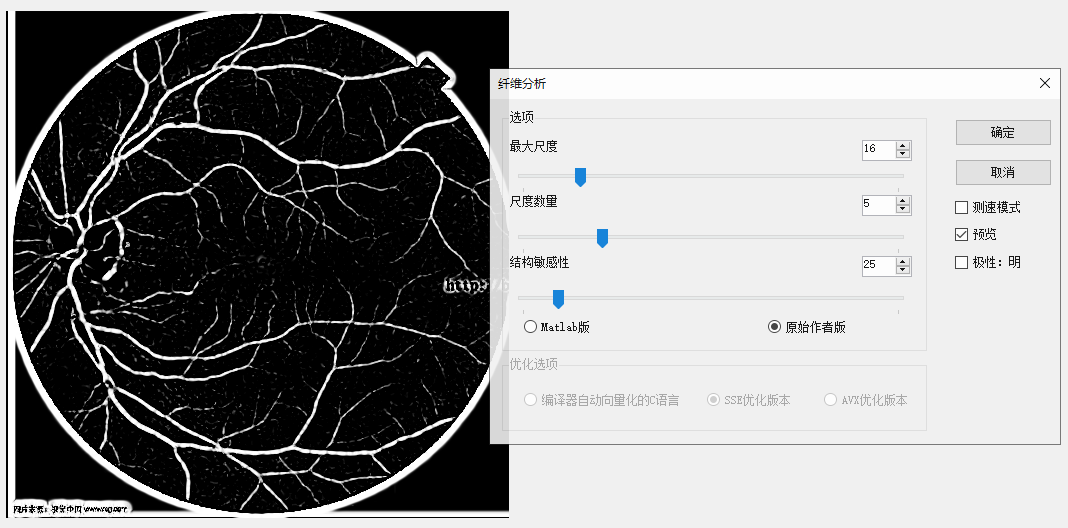
 　　　　　　　　　　　　　　同樣參數原始作者版本的結果，明顯沒有maltab的清晰　　

　　這個算法我測試確實對血管圖像的提取效果比較顯著，在貼幾個圖片。

　　　　　　

　　另外，在Halcon中有個lines_gauss函數，以前我就研究過他，並且小有成果，我現在可以100%肯定這個函數和我現在研究的這個東西有很大的關聯，也許在不久就可以把這個函數研究成功，因為，我們用lines_gauss這個常用的幾個圖片測試，會得到類似這樣的結果：

 

　　　　　　　　　　　　原圖　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　分析結果

　　  本文Demo下載地址：  https://files.cnblogs.com/files/Imageshop/SSE_Optimization_Demo.rar，本算法位於Detection(檢測相關）--》 FiberMetric（纖維分析） 菜單下，裏面的所有算法都是基於SSE實現的。

　　

計算機圖形學
user avatar hhhlxmh 頭像
點贊 1 用戶, 點贊了這篇動態!
點贊

Add a new 評論

Some HTML is okay.