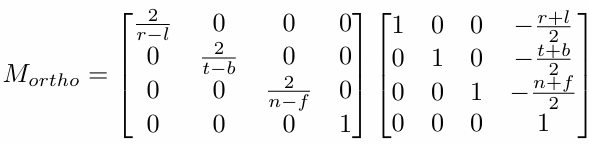計算機圖形學——Games101深度解析_第二章詳情 - 計算機圖形學 ENchantEd丨動態日志

三維旋轉的符號問題

旋轉矩陣的符號差異源於座標系的手系規則和旋轉方向定義。
首先是我們最常規的繞着z軸旋轉，這是右手系下的標準定義，符合"x軸轉向y軸"的正方向。

\[\mathbf{R}_z(\alpha) = \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]

這個時候，我們通常都把x軸與y軸線性變換之後所形成的角度設為$\alpha$ ,不同角的設置就會出現不同的符號，我們通常設置角的優先度就是x>y>z，所以就有了下面不同的符號。

X軸為基準軸：其旋轉矩陣最直觀，Y-Z平面完全遵循右手法則
Y軸次之：由於Y軸旋轉時Z-X平面的定義需保持座標系一致性，導致項符號反轉
Z軸最後：作為最常用的旋轉軸，其定義需兼容前兩者的嵌套結果。

\[\mathbf{R}_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]

\[\mathbf{R}_y(\alpha) = \begin{pmatrix} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]

歐拉角

我們把沿着每個角的旋轉角度分開來表示被稱之為歐拉角

[!note]
$\mathbf{R}_{xyz}(\alpha, \beta, \gamma) = \mathbf{R}_x(\alpha) \, \mathbf{R}_y(\beta) \, \mathbf{R}_z(\gamma)$

這裏挖坑：可以去探究下羅德里格斯旋轉公式是什麼，以及怎麼推導的，參考[數學]羅德里格旋轉公式（Rodrigues' rotation formula） - 知乎

視圖變換

相機放置的標準位置

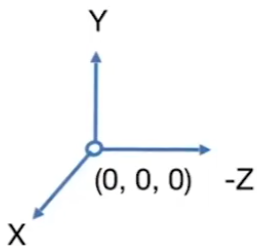
相機本體放在(0,0,0)上，正方向為-Z方向，正上方向為+Y方向，然後場景移動，而不是相機移動

視圖變換

有了這些概念之後我們就應該明白，即便我們要把相機放在世界座標系的原點上也是世界座標系移動，使得原點跑到了相機的座標上，而不是移動相機跑到原點上。那麼此刻我們感受到的應該是反客為主，此時相機的座標就是原點，而世界座標系才是需要移動的。

既然反客為主，這個時候世界座標系的原點也不一樣了，應該是相機視角下世界座標系原點的座標。比如，此刻相機的座標系為(10,5,3)，那麼此時原點現對於相機的座標為（$0-10,0-5,0-3$），或者一個物品此時的座標為(15,7,8)，那麼這個物品的相對座標就為：（15-10,7-5,8-3）。

所以想要把世界座標軸原點移動到相機就得直接減去相對座標才行。
那麼此時的變換矩陣就應該是$T_{view} = \begin{bmatrix}1 & 0 & 0 & -x_e \\0 & 1 & 0 & -y_e \\0 & 0 & 1 & -z_e \\0 & 0 & 0 & 1\end{bmatrix}$

當我們有了找個標準的視角之後，如果相機不是標準方向，那麼就需要我們把相機的視角旋轉到找個標準的位置。我們就要嘗試找到找個旋轉矩陣。但是這個矩陣肉眼並不好看出來，只能靠其他的辦法去求了。
我們雖然不知道怎麼直接拿到世界座標系旋轉到詳細座標系的旋轉矩陣，但是能知道怎麼把相機座標系的點怎麼在世界座標系來表示：

\[R = \begin{bmatrix} x_{\hat{g}\times\hat{t}} & x_t & x_{-g} & 0 \\ y_{\hat{g}\times\hat{t}} & y_t & y_{-g} & 0 \\ z_{\hat{g}\times\hat{t}} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

那麼表示起來就是這樣：$p_{\text{world}} = R \cdot p_{\text{camera}}$ 這裏的$p_{\text{camera}}$ 就是相機座標的點（基本座標 x 倍數 = 座標系下的座標），那麼我們要把世界座標轉換到相機座標只需要我們用$R^T R = R R^T = I$ 的性質對其進行轉換。
我們把$p_{\text{world}} = R \cdot p_{\text{camera}}$ 兩邊同時乘一個$R^T$ 那麼就出現了 $R^T \cdot p_{\text{world}} = RR^T \cdot p_{\text{camera}}$ 最後結果就是$$R^T \cdot p_{\text{world}} = p_{\text{camera}}$$
所以旋轉矩陣就是：

\[R^T=\begin{bmatrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0 \\ x_t & y_t & z_t & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

最後再加上平移矩陣，最後的總矩陣就是：

\[\begin{bmatrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & -x_e \\ x_t & y_t & z_t & -y_e \\ x_{-g} & y_{-g} & z_{-g} & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

透視投影與正交投影

正交投影

正交投影應該沒什麼可説的，很直觀，我們這裏只看一個東西。

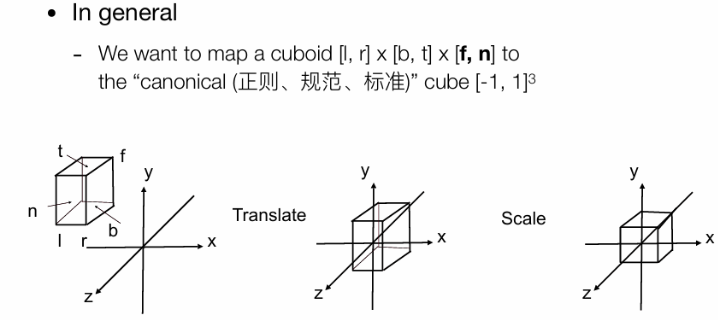
很多時候我們都把一個物體等價縮放到一個2x2的標準正方體裏面，如圖：

當然整個移動縮放矩陣就很清晰了

透視投影

我們重點還是透視投影。
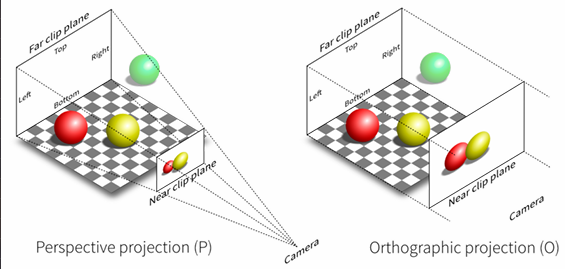
透視投影的核心概念是遠近縮放效應，即物體越遠，看起來越小。
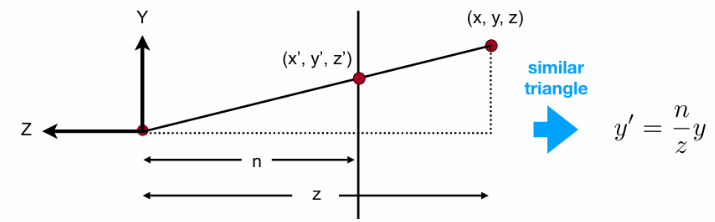
透視投影説白了就是個三角形，關係如下：

\[y' = \frac{n}{z} y, \quad x' = \frac{n}{z} x \]

其中：

(x,y,z)是原始三維座標
(x′,y′)是投影后的二維座標
n 是近平面的位置

這個關係説明，投影后的 x′,y′值與z 反比，物體越遠 (z 大)，投影座標越小。

這個時候我們希望有一個矩陣在齊次座標能夠表示到把$\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}$ 映射為 $\begin{pmatrix} \frac{nx}{z} \\ \frac{ny}{z} \\ \text{unknown} \\ 1 \end{pmatrix}$

讓我們一點一點地分析 ：

分析：

為什麼z軸的數值是unknown？

透視投影會改變 zz 的表現方式，在透視投影之後，我們仍然希望能夠正確地表示物體的深度 z 。
這個公式不能簡單地設為 $\frac{n}{z} z$，因為那樣會導致 z' 始終是 n，無法正確區分不同深度的物體。我們希望 z' 能保留某種線性變換形式，以便在深度緩衝（Z-buffer）等操作中使用。

變換矩陣的初步構造

為了方便計算我們將整個映射後的矩陣再乘以一個z

\[\begin{pmatrix} nx \\ ny \\ \text{still unknown} \\ z \end{pmatrix} \]

那麼這個變換矩陣就應該是這樣：

\[M_{\text{persp}\rightarrow\text{ortho}}\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} nx \\ ny \\ \text{still unknown} \\ z \end{pmatrix} \]

所以我們直接看都能看出來，x與y只用乘一個$n$ ，而最後保證和z的值一樣就行，所以就有了初步的結果：

\[M_{\text{persp}\rightarrow\text{ortho}}=\begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{pmatrix} \]

為什麼最後一行為(0,0,1,0)?

我們看到 $\begin{pmatrix} nx \\ ny \\ \text{still unknown} \\ z \end{pmatrix}$ 的最後一行實際上就是 $\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}$ 的z。

尋找第三行的關係

其中第三個分量 ? 就是新的 z'，它必須滿足以下要求：

必須是深度的線性函數，即形如 z′=Az+B
在近裁剪面 z = n 時，z' 應該保持為 n，以保證近裁剪面不會被誤判深度。
在遠裁剪面 z = f 時，z' 應該保持為 f，以保證遠裁剪面深度正確。

我們其實早就能發現z的值與xy的值是沒有關係的，
所以前面的兩個數都會是$(0,0,?,?)$
我們知道：

[!note] 近平面上的點 (z = n) 不能變動，即：

\[M_{\text{persp}\rightarrow\text{ortho}} \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ y \\ n^2 \\ 1 \end{pmatrix} \]

這表明，第三行應該是 $(0 \ 0 \ A \ B)$ 同時滿足：$An + B = n^2$

[!note] 遠平面上的點 (z = f) 不能變動：

\[Af + B = f^2 \]

通過解方程：

\[\begin{cases} An + B = n^2 \\ Af + B = f^2 \end{cases} \]

得到：

\[\begin{cases} A = n + f \\ B = -nf \end{cases} \]

所以，第三行最終確定為：

\[(0 \ ,0 \ ,(n+f) \ ,-nf) \]

最終的完整矩陣就為：

\[M_{\text{persp}\rightarrow\text{ortho}} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{pmatrix} \]

得到了這個投影之後在做一個正交投影就能直接投射到攝像機上

最後的思考題

[!note]
當空間中有一個點，在frustum內，但是不在近平面與遠平面上的時候，經過壓縮變換之後，這個點在Z軸上的座標，會變得離近平面更近、還是離遠平面更近、還是不變？

這裏的意思實際上是想讓我們思考：

在視錐體（frustum）內部、但不在近平面或遠平面上的一個點，
經過透視投影矩陣的壓縮變換後，
該點的 Z 軸座標是變得更靠近近平面，還是更靠近遠平面，還是不變？

解析

這個地方我們的第一反應就應該去求 Z 軸座標的值，這個地方實際上很好求，因為前面我們已經有了這樣一個旋轉矩陣了：$\begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{pmatrix}$ 。

我們設這個frustum內一點P的齊次座標為：$\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}$

變換後，得到新的齊次座標：

\[M_{\text{persp} \rightarrow \text{ortho}} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} nx \\ ny \\ (n+f)z - nf \\ z \end{pmatrix} \]

那麼我們的 z' = $\frac{(n+f)z - nf}{z} = (n+f) - \frac{nf}{z}$ ，其中 n < z < f

這個時候就很簡單了，我們只需要知道這個式子的單調性就能知道整個式子隨着 z’ 的增大是減小還是增加，如果是前者，那麼就是更靠近遠平面，反之亦然。也就是説，當 z 越發靠近 n ，變換後的值也會越小，越小，那麼離攝像機越近，離攝像機，那可不越靠近n嗎

這裏值得一提的是，這裏n，f，z都是大於0的，因為在攝像機視角中，只能看見正面，後面是看不見的，也不用進行處理，所以這裏的n，f，z一定都是大於0的。

這個式子不用多説，想知道單調性直接求個導就出來了：

\[\frac{d}{dz} z' = \frac{d}{dz} \left( (n+f) - \frac{nf}{z} \right) = \frac{nf}{z^2} \]

無論 z 等於何值，倒數都大於0，整個函數單調遞增。

透視投影的本質是“壓縮”遠處的深度範圍。
遠離近平面的點 z 變換後會向近平面擠壓，因為透視變換非線性縮小了遠處的深度範圍。
所有在 frustum 內的點，變換後 z′ 都比原來的 z 更靠近近平面。

問題解決。

ENchantEd丨動態日志

@ENchantedN

標簽

計算機圖形學 (20)

動態

計算機圖形學——Games101深度解析_第二章 - 動態詳情

三維旋轉的符號問題

歐拉角