動態

詳情 返回 返回

算法典型例題：N皇后問題，五種解法，逐步優化（遞歸版） - 動態 詳情

本文將介紹N皇后問題的五種解法，包括樸素回溯法、對稱優化、標記優化、可用優化、位運算優化，對於每種解題思路，提供相應的遞歸版代碼實現，最後將對每種解法進行測試，橫向對比每種解法的求解時間。

題目描述

在 N×N 格的國際象棋上擺放 N 個皇后，使其不能互相攻擊，即任意兩個皇后都不能處於同一行、同一列或同一斜線上，問有多少種擺法？

回溯法

解題思路

回溯法採用深度有限的搜索策略遍歷問題的解空間樹，可採用遞歸方式實現，也可採用非遞歸方式實現。本文提供的解題思路均採用遞歸法實現。

代碼實現

/**
 * N皇后問題：回溯法（所有下標均從1開始）
 * @param n 皇后的數量
 * @return 擺法的數量
 */
int queen(int n) {

    // 特判
    if (n == 1)return 1;

    // 棋盤  解的數量
    int q[n + 1], res = 0;
    memset(q, 0, sizeof q);

    // 判斷第k個皇后放置位置是否合適
    auto check = [&](int k) {
        for (int i = 1; i < k; ++i)
            // 同列、同斜線已存在皇后
            if (q[i] == q[k] || abs(q[i] - q[k]) == abs(i - k))return false;
        return true;
    };

    // 嘗試放置第i行
    function<void(int)> dfs = [&](int i) {
        if (i > n && ++res)return;
        q[i] = 0;
        while (++q[i] <= n) {
            if (!check(i))continue;
            dfs(i + 1);
        }
    };

    // 嘗試放置第一行
    dfs(1);

    return res;
}

時間複雜度：O(n^{n^n})。

空間複雜度：O(n)。

對稱優化

解題思路

仔細觀察N-皇后的解，發現一種方案可以通過“對稱”得到另一種方案。以“左右對稱”為例，當 N=5，限定第一行皇后在左邊一半區域時，方案數為 6，如圖 1 所示。

（N皇后的可行解存在七種對稱關係，此處僅討論左右對稱。）

圖1

通過“左右對稱”可以獲得另一方案，同時發現，後面有兩種方案重複，去除重複方案後，剩下的剛好是 N=5 時的全部方案，如圖 2 所示。

圖2

當 N 為偶數時關於中間那條線對稱，當 N 為奇數時關於中間那一列對稱。利用左右對稱可以使得工作量減少一半，為此，在放置皇后時，增加兩條限制

  1. 第一行的皇后只放在左邊一半區域，也即位置小於等於 (n+1)/2；
  2. 當 N 為奇數且第一行皇后剛好放在 (n+1)/2 位置（即中間）時，為避免重複，第二行皇后必須放在左邊一半區域。

代碼實現

/**
 * N皇后問題：對稱優化（所有下標均從1開始）
 * @param n 皇后的數量
 * @return 擺法的數量
 */
int queen(int n) {

    // 特判
    if (n == 1)return 1;

    // 棋盤 中點位置 解的數量
    int q[n + 1], w = (n + 1) >> 1, res = 0;
    memset(q, 0, sizeof q);

    // n是否為奇數
    bool odd = n & 1;

    // 判斷第k個皇后放置位置是否合適
    auto check = [&](int k) {
        for (int i = 1; i < k; ++i)
            // 同列、同斜線已存在皇后
            if (q[i] == q[k] || abs(q[i] - q[k]) == abs(i - k))return false;
        return true;
    };


    // 嘗試放置第i行，第i行放置的上限為k
    function<void(int, int)> dfs = [&](int i, int k) {
        if (i > n && ++res)return;
        // 嘗試放置第i行的每個位置
        q[i] = 0;
        while (++q[i] <= k) {
            if (!check(i))continue;
            // 第1行放中間時，第2行必須放左邊
            if (odd && i == 1 && q[1] == w)dfs(2, w - 1);
            else dfs(i + 1, n);
        }
    };

    // 第1行的上限為w
    dfs(1, w);

    return res << 1;
}

時間複雜度：O(n^{n^n})。

空間複雜度：O(n)。

標記優化

解題思路

對於棋盤單元座標，有如下規律（圖 2 為兩個 4×4 的棋盤）：

  1. 同一正斜線所佔據的單元的橫縱座標之和相等。
  2. 同一反斜線所佔據的單元的橫縱座標之差相等。

圖3

由此，可以設置數組 L 和 R，表示斜線的佔有情況，從而可以做到快速判斷某位置是否可以放置皇后。

① L[i] 表示和為 i 的正斜線是否被佔據，i 的範圍為 [2,2N]，故 0,1兩個位置捨去不用。

② R[i] 表示差為 i 的反斜線是否被佔據，i 的範圍為 [1-N,N-1]，為避免負下標，對 i 作加 N 處理。

L[i] 中的 i 捨去 0,1 兩個位置，R[i] 中的 i 加 N 而不是加 N-1，都是為了減少計算量。

同時，再設置數組 Y，Y[i] 表示第 i 列是否被佔據，1≤i≤N。改用根據數組 L,R,Y 來判斷某位置是否可以放置皇后，可減少大量判斷。（ Y[i] 中的 i 不從 0 開始是為了便於處理）。

此處統一約定，對於標誌數組 L,R,Y，值為 1 表示佔用，值為 0 表示未佔用。以 L 為例，L[i]=1 表示正斜線 i 被佔用。

代碼實現

/**
 * N皇后問題：標記優化（所有下標均從1開始）
 * @param n 皇后的數量
 * @return 擺法的數量
 */
int queen(int n) {

    // 特判
    if (n == 1)return 1;

    // 棋盤 列 左斜線 右斜線
    int q[n + 1], y[n + 1], l[(n << 1) + 1], r[(n << 1) + 1];

    memset(q, 0, sizeof q);
    memset(y, 0, sizeof y);
    memset(l, 0, sizeof l);
    memset(r, 0, sizeof r);

    // 中點位置 擺法數量
    int w = (n + 1) >> 1, res = 0;
    // n是否為奇數
    bool odd = n & 1;

    // 檢查(i,j)是否可以放置皇后
    auto check = [&](int i, int j) {
        // 同列/左斜線（反斜線）/右斜線（正斜線）已存在皇后
        if (y[j] || l[i - j + n] || r[i + j])return false;
        // 同列、左斜線、右斜線標記為不可放置
        y[j] = l[i - j + n] = r[i + j] = 1;
        // 在(i,j)位置放置皇后
        q[i] = j;
        return true;
    };

    // 嘗試放置第i行，第i行放置的上限為k
    function<void(int, int)> dfs = [&](int i, int k) {
        if (i > n && ++res)return;
        // 嘗試放置第i行的每個位置
        for (int j = 1; j <= k; j++) {
            if (!check(i, j))continue;
            // 第1行放中間時，第2行必須放左邊
            if (odd && i == 1 && q[1] == w)dfs(2, w - 1);
            else dfs(i + 1, n);
            // 同列、左斜線、右斜線標記為可放置
            y[j] = l[i - j + n] = r[i + j] = 0;
        }
    };

    // 第1行的上限為w
    dfs(1, w);

    return res << 1;
}

時間複雜度：O(n^n)。

空間複雜度：O(n)。

可用優化

解題思路

前面兩種實現，總是從當前行的第一個位置開始嘗試，即使當前行沒有位置可以放置，也需嘗試完當前行每一個位置，這顯然是沒有必要的。新增 next 數組，next[i] 表示位置 i 的下一個可用位置（可用列），next[0] 表示第一個可用位置，next[i]=0 表示 i 是最後一個可用位置，特別的，next[0]=0 表示無可用位置，此時需要回溯。既然已經知道哪些位置可用，那就不再需要數組 Y 來判斷某列是否可用。

代碼實現

/**
 * N皇后問題：可用優化（所有下標均從1開始）
 * @param n 皇后的數量
 * @return 擺法的數量
 */
int queen(int n) {

    // 特判
    if (n == 1)return 1;

    // 棋盤 列 左斜線 右斜線
    int q[n + 1], nex[n + 1], l[(n << 1) + 1], r[(n << 1) + 1];

    memset(q, 0, sizeof q);
    for (int i = nex[n] = 0; i < n; ++i) nex[i] = i + 1;
    memset(l, 0, sizeof l);
    memset(r, 0, sizeof r);

    // 中點位置 擺法數量
    int w = (n + 1) >> 1, res = 0;
    // n是否為奇數
    bool odd = n & 1;

    // 嘗試放置第i行，第i行放置的上限為k
    function<void(int, int)> dfs = [&](int i, int k) {
        if (i > n && ++res)return;
        // cur 下一個可放置的位置 pre cur的前一個位置
        int pre = 0, cur = nex[pre];
        while (cur > 0 && cur <= k) {
            if (!l[i - cur + n] && !r[i + cur]) {
                // 左斜線、右斜線置為不可放置
                l[i - cur + n] = r[i + cur] = 1;
                // 在(i,cur)位置放置皇后
                q[i] = cur;
                // 刪除cur
                nex[pre] = nex[cur];
                // 第一行棋子放中間時
                if (odd && i == 1 && q[1] == w)dfs(2, w - 1);
                else dfs(i + 1, n);
                // 將cur添加回備選位置
                nex[pre] = cur;
                // 左斜線、右斜線置為可放置
                l[i - cur + n] = r[i + cur] = 0;
            }
            // 下一節點的前導
            pre = cur;
            // 下一節點
            cur = nex[pre];
        }
    };

    // 第1行的上限為w
    dfs(1, w);

    return res << 1;
}

時間複雜度：O(n!)。

空間複雜度：O(n)。

位運算

解題思路

以 3×3 的棋盤為例，最左上角的左斜線記作第一條左斜線，最右上角的第一條右斜線記作第一條右斜線。為了便於敍述，以下涉及到的二進制均只有 n 位（棋盤大小），第幾位是從左往右數。

將列、左斜線（/）、右斜線（\）的可用狀態分別用二進制表示，1 表示佔用，0 表示可用，以列為例，010 表示第 1,3 列可用，第 2 列佔用。

將斜線狀態轉換為列狀態，以左斜線為例，如下表所示

第1行 第2行 第3行
第1條左斜線 100 000 000
第2條左斜線 010 100 000
第3條左斜線 001 010 100
第4條左斜線 000 001 010
第5條左斜線 000 000 001

（第 1 條左斜線，第 1 行）= 100 的解釋為，若第 1 條左斜線不可用，對於第 1 行的影響是 100，即，第 1 列不能放置，第 2,3 列可以放置。

對於第 i 行而言，必須要放置一個皇后（放置不了就直接回溯了），放置完皇后，其對應左斜線狀態必然不是 000，因為放置的這個皇后必然會導致某左斜線不可用，所以，假設第 i 行到第 i+1 行，左斜線狀態狀態由 A➡B，則 A 必定不為 000，在上表所有狀態轉換（由第 j 行到第 j+1）中，排除起始狀態為 000 的轉換，(i,j+1) 可由 (i,j) 左移一位得到。

同理可得，對於右斜線而言，(i,j+1) 可由 (i,j) 右移一位得到。

設考慮第 i 行時，列、左斜線、右斜線狀態分別為 C,L,R，則

  • 第 i 行可選的位置為 pos = ~(C | L | R) & ((1<<n)-1) 的二進制中 1 對應的列，假設選的是第 k 列，則記為 P，P 的二進制中只有第 k 位為 1。
  • 考慮第 i 行時，C = C|P，L = (L|P)<<1，R = (R|P)>>1。

注意，C,L,R 需要始終保持只有 n 位有效，由於整數 int 有 32 位，那麼除開低 n 位，其餘各位均需保持為 0。

代碼實現

/**
 * N皇后問題：位運算
 * @param n 皇后的數量
 * @return 擺法的數量
 */
int queen(int n) {
    int res = 0, mk = (1 << n) - 1;
    // c 列 l 左斜線  r 右斜線
    function<void(int, int, int)> dfs = [&](int c, int l, int r) {
        // 每行都放完則列狀態低n位均為1，即等於mk
        if (c == mk && ++res)return;
        // 放置的位置
        int pos = ~(c | l | r) & mk, p;
        while (pos) {
            // 取pos最低位的1
            p = pos & (-pos);
            // 將pos最低位的1置為0
            pos &= pos - 1;
            // 放置第k+1行
            dfs(c | p, (l | p) << 1, (r | p) >> 1);
        }
    };
    // 列、左斜線、右斜線初始狀態均為0，即均未被佔用
    dfs(0, 0, 0);
    return res;
}

時間複雜度：O(n!)。

空間複雜度：O(n)。

統計與分析

五種解法均採用遞歸實現，為了直觀比較五種解法的效率，分別統計五種解法在 N=10 到 N=18 的情況下的求解時間（單位為毫秒），測試結果如下表所示。

解法\N 10 11 12 13 14 15 116 17 18
回溯法 4 29 163 1000 6418 43895 313615 2382453 18972771
對稱優化 2 14 74 447 2864 19986 142508 1096171 8902861
標記優化 0 16 32 270 1589 10214 70769 512974 3898774
可用優化 1 4 21 124 726 4513 31100 221271 1633623
位運算 0 4 24 135 774 4905 33137 242848 1889411

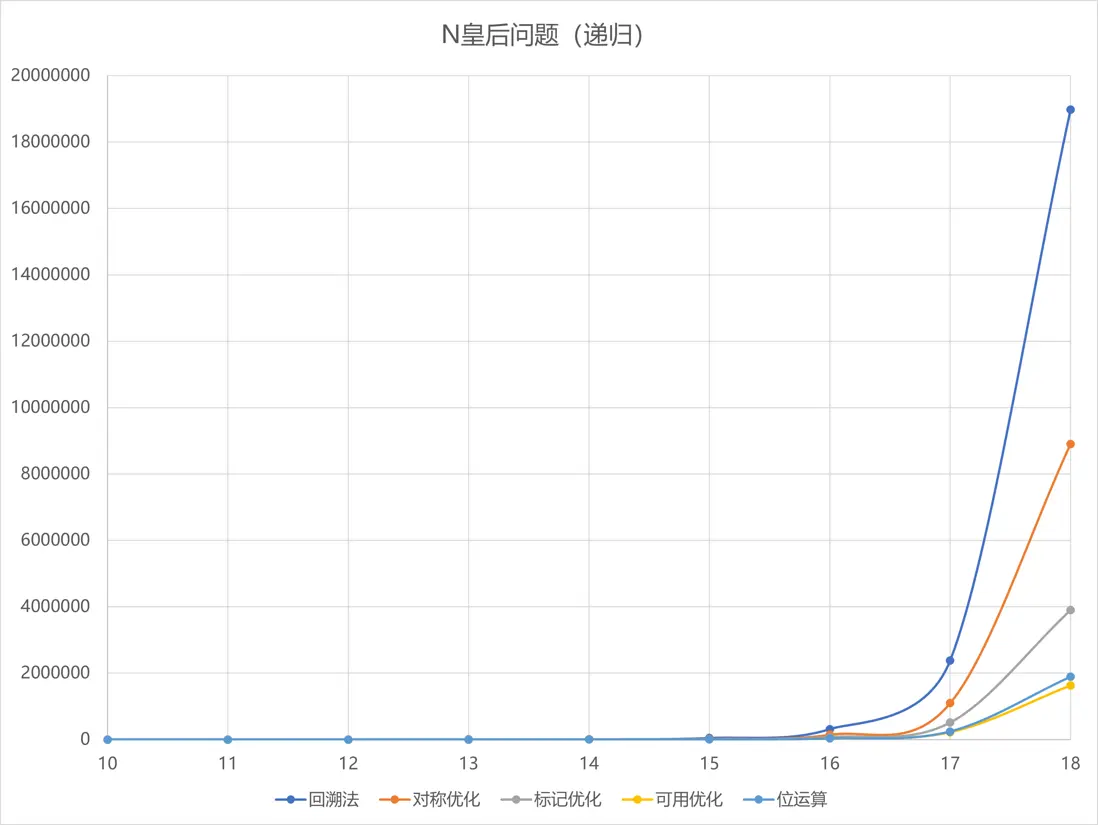
根據上表數據製作散點圖，如圖 4 所示：

圖4 N皇后問題遞歸求解時間散點圖

從回溯法到可用優化，通過逐步優化求解方式，求解時間也顯著減少。位運算方式的求解時間略高於可用優化，但大致相當。

END

文章文檔：公眾號 字節幺零二四 回覆關鍵字可獲取本文文檔。

算法 , 遞歸 , 回溯法
user avatar u_17513518 頭像 yuanfang_648a85b26d85e 頭像 AmbitionGarden 頭像 u_16769727 頭像 lenglingx 頭像 jiangyi 頭像 chuanghongdengdeqingwa_eoxet2 頭像 lvlaotou 頭像 jkdataapi 頭像 huangxunhui 頭像 meituanjishutuandui 頭像 chenjiabing666 頭像
點贊 26 用戶, 點贊了這篇動態!
點贊

Add a new 評論

Some HTML is okay.