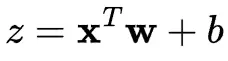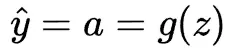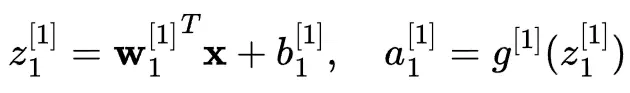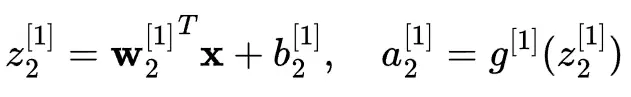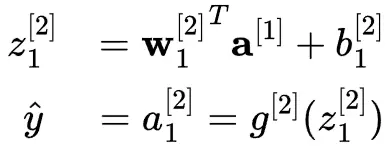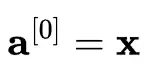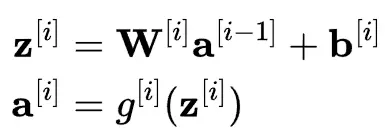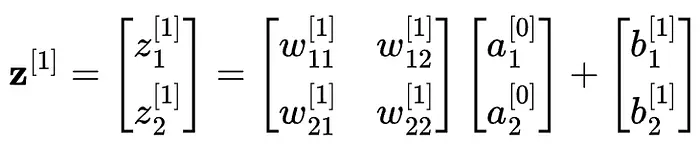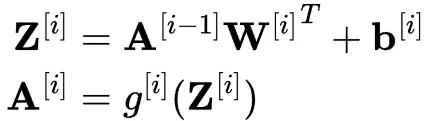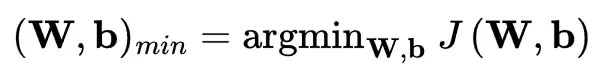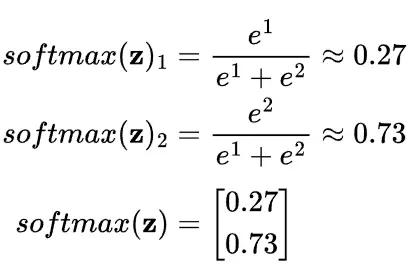本文簡單介紹了神經網絡的基本原理、組成和基礎算法，並通過示例介紹了最簡單的神經網絡是如何工作的。原文：Learn How Neural Networks Work

神經網絡是人工智能中最重要的組成部分之一，若沒有神經網絡，像 ChatGPT 這樣的大語言模型就不會存在。實際上，幾乎所有深度學習模型都在某種程度上使用了神經網絡。

這就是為什麼瞭解神經網絡的工作原理如此重要。所以，讓我們重温一下機器學習的基礎知識吧。

神經網絡

神經網絡是一種受人類大腦工作原理啓發而設計的機器學習模型，由許多被稱為神經元（neuron）的小單元組成，這些神經元以層的形式相互連接。

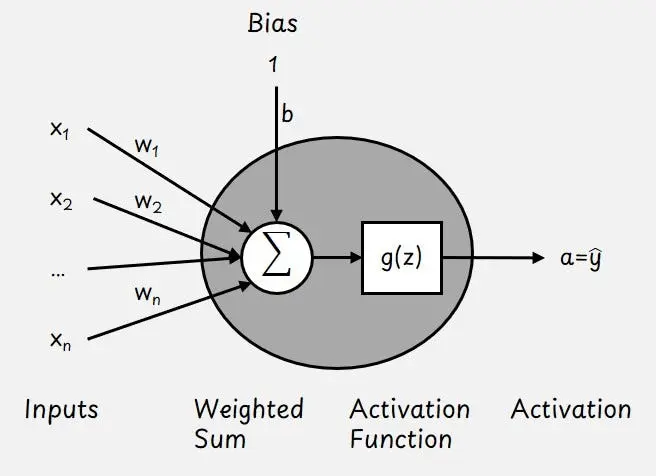
我們從最簡單的神經網絡開始講起，這種網絡只有一個神經元，下圖展示了其具體的樣子。

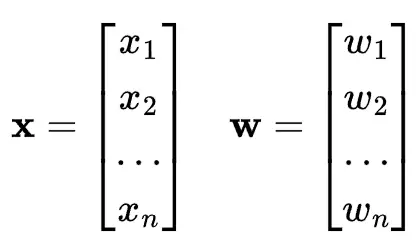
神經元包括輸入特徵向量x，可學習權重參數向量w和可學習偏置b。

這些參數幫助神經元確定每個輸入的重要性。

我們首先計算輸入的加權和：

然後通過激活函數g(z)變換輸出值z。該函數幫助網絡學習非線性模式。神經元的輸出稱為激活a，在只有一個神經元的情況下，也是模型的輸出預測。

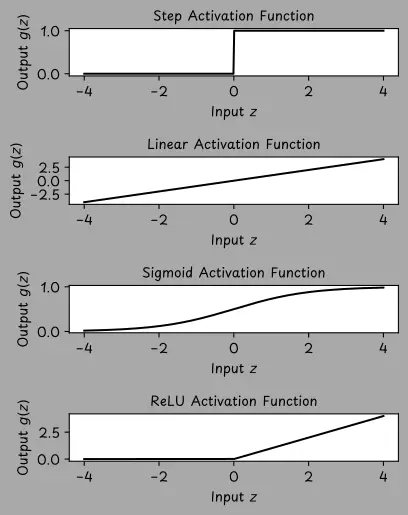
在神經網絡中有幾種可能的激活函數，每種函數都有不同性質，下圖顯示了4個示例。

• 在早期的一種被稱為“感知機（perceptron）”的神經網絡中，使用了階梯激活函數（step activation function）。當輸入值 z 大於 0 時，神經元會“觸發”（輸出 1），否則會處於關閉狀態（輸出 0）。
• 線性激活函數（linear activation function） g(z) = z 與完全不使用激活函數的效果相同。在只有一個神經元的網絡中，會產生線性迴歸模型。
• Sigmoid 激活函數 g(z) = sigma(z) 將任何輸入值轉換為 0 到 1 之間的範圍，這在我們想要建模概率時特別有用。當與單個神經元一起使用時，為我們提供了邏輯迴歸模型。
• 修正線性單元（ReLU，rectified linear unit） 是一種定義為 g(z) = max(z, 0) 的激活函數。是深度學習中最廣泛使用的激活函數。如果輸入是正數，ReLU 會讓其通過。如果輸入是負數，ReLU 輸出 0。

根據激活函數的不同，單個神經元可以執行分類或迴歸任務。例如，它可以表現得像線性或邏輯迴歸模型。這些都是具有特定激活選擇的神經元的特殊情況，從而使得單個神經元成為一種簡單但靈活的構建模塊。然而，神經網絡真正的強大之處在於將眾多神經元連接在一起。

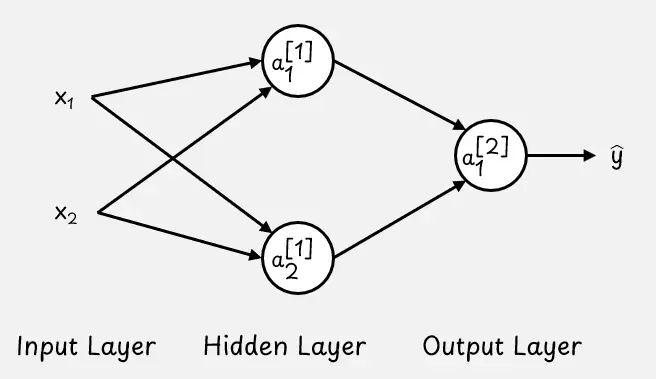
現在，我們不再侷限於單個神經元，而是來探討當多個神經元相互連接形成具有若干層的神經網絡時情況會如何變化。請看下圖示例。這個網絡有三層：

• 輸入層，即數據進入網絡的地方。
• 隱藏層，用於進行中間計算。
• 輸出層，用於生成最終結果。

雖然一共有三層，但在描述網絡深度時，只計算隱藏層和輸出層，因此被稱為兩層神經網絡。這種類型的網絡也被稱為 前饋神經網絡（feedforward neural network） 或 多層感知器（MLP，multi-layer perceptron）。

在這個例子中，隱藏層和輸出層都是全連接的。在全連接層（也稱為密集層）中，每個神經元都與前一層中的每個神經元相連接。

上述圖中的每個圓都代表一個神經元，該神經元具有權重 w、偏差 b 以及激活函數 g(z)。為簡便起見，未明確標註偏差和激活函數符號。

現在來看一下如何計算隱藏層中的激活值。

對於隱藏層中的第一個神經元：

對於隱藏層中的第二個神經元：

然後用前一層的激活作為輸入來計算輸出層的激活：

深度神經網絡通常具有多種特徵、多個隱藏層以及一個或多個輸出單元。而“深度”一詞僅僅表示該網絡具有不止一個隱藏層。

網絡的層數和神經元數量越多，就越能學習複雜的模式。然而，更大的網絡需要學習的參數也更多。這就增加了對更多訓練數據和計算能力的需求，以便有效訓練該網絡。

設計一個神經網絡需要做出一系列重要決策，例如：

• 應包含多少隱藏層（這被稱為網絡的深度）。
• 每層有多少神經元（即網絡的寬度）。
• 應使用何種激活函數。
• 還有許多其他設計細節。

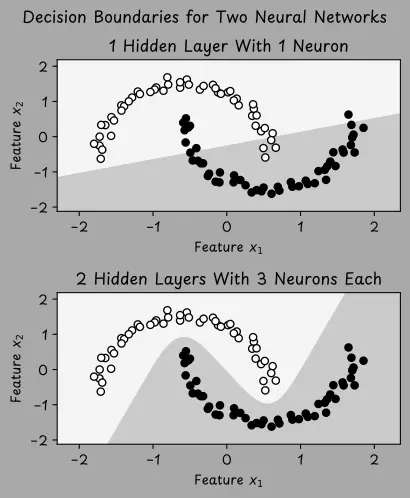
為了説明設計選擇對學習的影響，我們通過下圖演示一個視覺案例。數據集包含兩個類別（標籤 y 可以是 1 或 0），這些點以類似月亮的形狀排列。

上方的圖展示了一個具有一個隱藏層和一個神經元的小型神經網絡，它試圖對數據進行分類。然而，該網絡僅學習到一個簡單的直線邊界，並不足以區分曲線形狀。相比之下，下方的圖展示了一個更大的網絡，有兩層隱藏層，每層有三個神經元。這個網絡學習到了一個非線性邊界，能夠更好的適配數據。

為了減少大型神經網絡模型中的過擬合現象，一種常用的正則化策略是“隨機失活”。在訓練過程中，隨機失活會隨機“關閉”（通過將激活值乘以零）網絡中一定比例的神經元，可以防止模型過度依賴特定神經元，並促使它學習更通用、更穩健的特徵。

矩陣表示法

隨着神經網絡規模的擴大以及數據集容量的增加，單獨對每個神經元進行計算變得過於緩慢且效率低下。為了提高效率，我們採用矩陣乘法。

首先將輸入特徵定義為第 0 個激活值：

對於神經網絡中的每一層，可以使用以下兩個方程：

我們來分步驟説明：

• $z^{[i]}$：用於計算第 i 層加權總和的向量。
• $W^{[i]}$：連接第 [i-1] 層與第 i 層的權重矩陣。此矩陣形狀為第 i 層中的神經元數量乘以第 i-1 層的輸入數量。
• $a^{[i-1]}$：前一層的激活值是當前層的輸入。
• $b^{[i]}$：第 i 層的偏置項向量。
• $g^{[i]}$：第 i 層的激活函數，例如 ReLU 或 Sigmoid。
• $a^{[i]}$：第 i 層的輸出向量（激活值）。

例如，在我們的神經網絡示例中，這裏是如何計算第一層（i=1）的 z 的值的：

到目前為止，我們只研究了一個數據點。然而在實踐中，我們經常希望一次處理一整批數據，這可以通過矩陣乘法完成。

如果將所有輸入向量堆疊到一個矩陣 X 中，每一行代表一個輸入，那麼可以一次計算所有激活：

注意：

• Z 和 A 現在是矩陣形式，每一行代表一個樣本。
• 通過 $W^{[i]^T}$（權重矩陣的轉置），以使維度匹配。
• 偏置向量會添加到每一行（稱為廣播操作）。

這種基於矩陣的方法使得深度學習既高效又可擴展，無需逐個遍歷神經元，而是可以一次性計算所有輸出。這對於 GPU 來説非常理想，因為 GPU 專門設計用於同時處理數千次矩陣運算。

這就是現代人工智能模型能夠處理海量數據並擁有數百萬（甚至數十億）參數的原因：因為在其內部運作機制下，不過就是進行大量快速運算的矩陣數學運算而已。

訓練神經網絡

神經網絡通過調整其參數 W 和 b 來學習，以最小化成本（或損失）函數 J(W,b)，該函數會計算訓練數據集上的平均預測誤差。

具體成本函數取決於任務類型以及在輸出層所使用的激活函數。分類任務通常採用交叉熵損失，而回歸任務則使用均方誤差。

訓練始於初始化階段。通常情況下，偏置項會被設為零，而權重則會以符合均勻分佈或正態（高斯）分佈的較小隨機值進行初始化。這種隨機性有助於打破對稱性，並使每個神經元能夠學習不同內容。

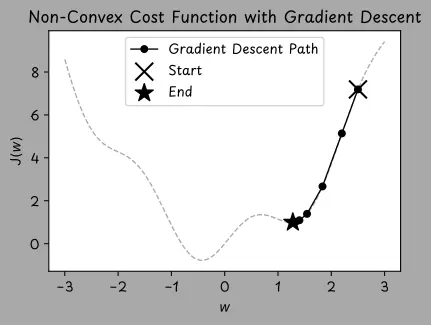
初始化完成後，用一種名為梯度下降的優化算法逐步調整權重和偏置值。梯度下降通過逐步小幅調整模型的權重和偏置值（朝着能減少誤差的方向），來最小化成本函數，有點像沿着山谷的坡面向下走，以找到谷底的位置。

Softmax

在許多機器學習任務中，尤其是在分類任務中，神經網絡並非僅僅生成單一輸出結果。相反，會生成完整的輸出向量，針對每個可能類別分別生成一個輸出值。例如，ImageNet 數據集曾是深度學習在圖像識別領域的早期基準測試，包含的圖像可能屬於 1000 個類別中的某一個。因此，基於 ImageNet 進行訓練的神經網絡的輸出層必須生成 1000 個分數，每個類別對應一個分數。

我們用 softmax 函數將這些原始分數轉換為概率值。softmax 函數將實數向量轉換為概率分佈，每個輸出值都在 0 到 1 之間，且所有輸出值總和為 1。因此，softmax 函數通常被用作分類模型輸出層的激活函數。

對於輸入向量 z ，softmax 函數的計算過程為：

z_i 的值越高，其對應 softmax 輸出就越大，但所有輸出都是相對於向量中的其他值而言的。

這些值 z_i 通常被稱為“對數機率”，是機器學習模型在經過 softmax 函數轉換為概率之前所產生的原始分數。

Softmax 示例：

對於 z = [1, 2] 的 softmax 計算結果為：

現在有兩個相加起來等於 1 的概率：0.27 + 0.73 = 1 。

神經網絡的實際應用

在 Python 中，可以使用 sklearn 中的 MLPClassifier 來訓練基本的神經網絡。

定義網絡並僅基於訓練數據對其進行訓練，只需要幾行代碼即可完成。

首先加載示例數據集，將其分為訓練集和測試集，並對特徵進行標準化處理。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score

# 創建測試數據集
X, y = make_moons(n_samples=300, noise=0.1, random_state=42)

# 將數據集分為訓練集和測試集（70% 訓練，30% 測試）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 標準化特徵（在機器學習中非常重要）
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)

然後構建一個具有一個隱藏層的簡單神經網絡，該隱藏層包含兩個神經元。隱藏層採用 ReLU 激活函數。輸出層會自動使用 softmax 激活函數，該函數在進行預測時能給出概率值。

訓練過程是通過在訓練數據集上調用模型的 fit() 函數來完成，該函數會最小化成本函數。

# 為神經網絡設定超參數
hidden_layer_depth = 1  # 隱藏層數量
hidden_layer_width = 2  # 每個隱藏層中的神經元數量

# 創建表示隱藏層大小的元組
hidden_layer_sizes = (hidden_layer_width,) * hidden_layer_depth

# 在訓練數據集上訓練神經網絡
mlp = MLPClassifier(hidden_layer_sizes=hidden_layer_sizes, 
                    activation='relu',  # 隱藏層激活函數
                    solver='sgd',  # 優化算法
                    max_iter=2000)
mlp.fit(X_train, y_train)

神經網絡已經完成訓練，我們來進行一些預測。

# 進行預測並評估測試集的準確率
y_pred = mlp.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f'Test Accuracy: {accuracy * 100:.2f}%')

最後，可以將訓練結果可視化。

# Create meshgrid for decision boundary visualization
x_min, x_max = X_test[:, 0].min() - 0.5, X_test[:, 0].max() + 0.5
y_min, y_max = X_test[:, 1].min() - 0.5, X_test[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),
                     np.linspace(y_min, y_max, 300))
grid = np.c_[xx.ravel(), yy.ravel()]


# Get probabilities for the grid points to plot decision boundaries
probs = mlp.predict_proba(grid)[:, 1].reshape(xx.shape)


fig, axes = plt.subplots(1, 2, figsize=(12, 6))

# Visualize the decision boundary
ax1 = axes[0]
ax1.contourf(xx, yy, probs, levels=[0, 0.5, 1], alpha=0.3, cmap=plt.cm.Greys)
ax1.scatter(X_test[:, 0], X_test[:, 1], c=y_test, cmap=plt.cm.Greys, edgecolors='k', s=60)
ax1.set_title(f'Decision Boundary\n'
              f'Hidden Layers: {hidden_layer_depth}, Neurons per Layer: {hidden_layer_width}')
ax1.set_xlabel('Feature $x_1$')
ax1.set_ylabel('Feature $x_2$')


# Plot the training loss curve
ax2 = axes[1]
ax2.plot(mlp.loss_curve_)
ax2.set_title('Training Loss Curve')
ax2.set_xlabel('Iteration')
ax2.set_ylabel('Loss')
ax2.grid(True)

# Adjust layout for better visualization
plt.tight_layout()
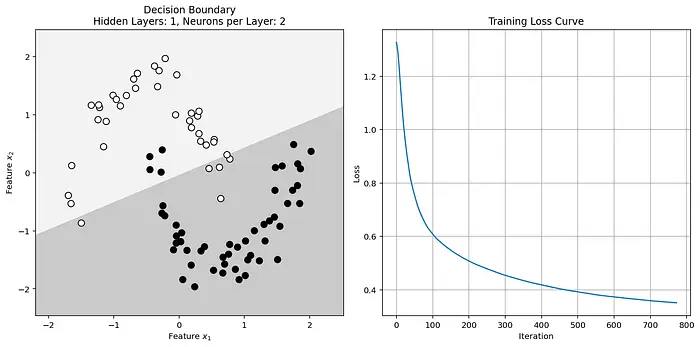
plt.show()

輸出如下結果：

該決策邊界不夠複雜，無法將數據區分開來。因此，應當通過增加神經網絡的深度和/或寬度來提高其複雜度。

你好，我是俞凡，在Motorola做過研發，現在在Mavenir做技術工作，對通信、網絡、後端架構、雲原生、DevOps、CICD、區塊鏈、AI等技術始終保持着濃厚的興趣，平時喜歡閲讀、思考，相信持續學習、終身成長，歡迎一起交流學習。為了方便大家以後能第一時間看到文章，請朋友們關注公眾號"DeepNoMind"，並設個星標吧，如果能一鍵三連(轉發、點贊、在看)，則能給我帶來更多的支持和動力，激勵我持續寫下去，和大家共同成長進步！

本文由mdnice多平台發佈