近年來,機理與數據的融合計算正快速發展着。機器學習作為數據驅動的計算方法,以其解決高維複雜問題的能力而聞名於世。它在視覺理解、自然語言處理等領域取得了重大突破。與此同時,基於機理的計算方法,如有限元模擬,在現代工業中起着至關重要的作用,廣泛應用於飛機、汽車、材料和新能源等行業。
有限元方法簡介與挑戰
有限元法(FEM,Finite Element Method)是一種為求解偏微分方程邊值問題近似解的數值技術。求解時對整個問題區域進行分解,每個子區域上定義基函數,把有限元組合起來近似得到原方程的解。然而,被廣泛應用的有限元方法也面臨挑戰:隨着問題規模的增長,計算複雜度和內存需求也隨之增加,導致計算時間過長和資源消耗過大(“維度災難”問題)。
逆問題是在數學和科學中,通過給定輸出數據,尋找導致這些結果的輸入或參數。求解逆問題的價值在於提供無法直接觀測的信息和改善決策預測。有限元在許多逆問題中是常用的求解方法,然而逆問題中,用有限元法求解會有很多難點:
1. 非唯一性:可能存在多個不同的輸入或參數組合對應相同的觀測結果,無法得到唯一解決方案。
- 不適定問題:輸入數據中的誤差會放大,導致求解結果不穩定。
- 計算複雜度高:特別是在高維度或複雜模型下,計算複雜度顯著增加。
機器學習在 FEM 中的應用與痛點
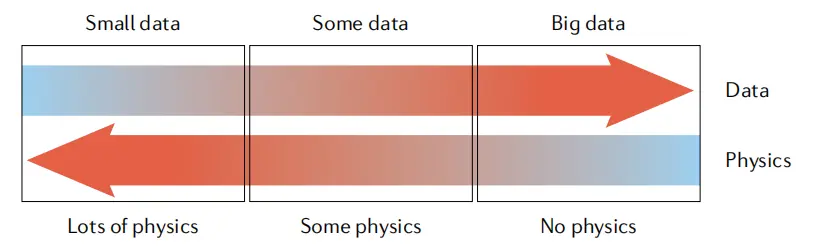
機器學習(Machine Learning, ML)通過從數據中總結規律,並使用大量參數進行學習,有潛力更好地處理複雜、大規模數據,並在非線性建模上有優勢,推動科學和工程進步,高效地解決"維數災難"。例如,神經網絡和深度學習可以用於預測、優化和模擬 FEM 計算過程,以及解決逆問題。然而,在實際應用中,ML 算法面臨一些挑戰。由於其"黑箱"性質、訓練困難、分佈外難泛化和數據缺乏等問題,機器學習方法無法直接應用於嚴肅科學場景。於是機理與數據融合計算就變得尤為重要,它試圖在保持物理準確性和性能之間取得平衡,使人們對科學的認識可以轉化為大規模可應用的程序與系統。
數據與機理融合計算,圖片來自Physics-informed machine learning
然而,機理與數據融合計算在實際應用中遇到了許多困難,新興的機器學習框架和傳統有限元框架往往不兼容。初學者甚至有經驗的專家們常常會遇到以下問題:
- Python 程序速度過慢而 C/C++/Fortran 開發與調試難度過高;
- 手動計算微分和 Sensitivity 非常麻煩且容易犯錯;
- 在研究數據驅動的計算問題時,需要使用多個工具並在它們之間頻繁傳輸數據,非常繁瑣。
Notebook 上手實踐
它來了它來了,JAX-FEM: A differentiable GPU-accelerated 3D finite element solver 帶着它的三大優勢來了:
- Life Is Short, Use Python! JAX-FEM 使用純 Python 實現,同時可利用 GPU 以高效地解決中等到大規模問題。
-
利用 JAX 的可微編程實現高效便捷的逆向設計。
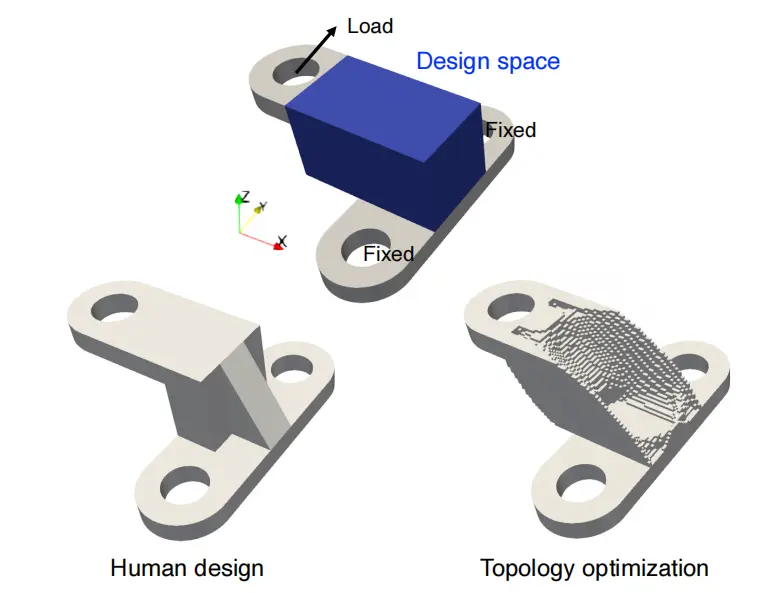
逆問題:拓撲優化示例 -
可以與機器學習無縫集成。無須在不同框架下切換開發。
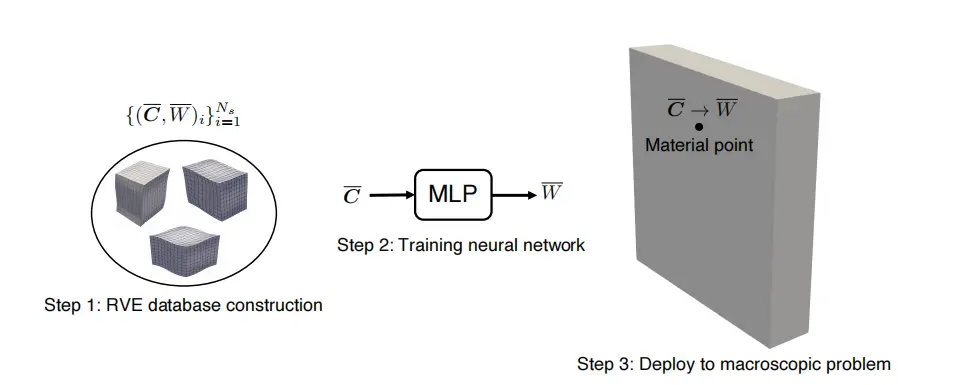
JAX-FEM實現的數據驅動的多尺度計算方案工作流示意圖現在點擊下方圖片來開始閲讀吧!
歡迎大家來 Notebook 案例廣場,獲取更多有意思的實踐~