🏆🏆🏆教程全知識點簡介:基礎篇 1. 二分查找 2. 冒泡排序 7. ArrayList 8. Iterator 9. LinkedList 10. HashMap 1)基本數據結構 2)樹化與退化 3)索引計算 4)put 與擴容 5)併發問題 11. 單例模式 併發篇 1. 線程狀態 3. wait vs sleep 4. lock vs synchronized 虛擬機篇 1. JVM 內存結構 4. 內存溢出 5. 類加載 6. 四種引用 7. finalize 框架篇 1. Spring refresh 流程 2. Spring bean 生命週期 6. Spring 註解 7. SpringBoot 自動配置原理 數據庫篇 1. 隔離級別 2. 快照讀與當前讀 3. InnoDB vs MyISAM 4. 索引 索引基礎 5. 查詢語句執行流程 6. undo log 與 redo log 7. 鎖 緩存篇 1. Redis 數據類型 2. keys 命令問題 3. 過期 key 的刪除策略 5. 緩存問題 6. 緩存原子性 7. LRU Cache 實現 分佈式篇 1. CAP 定理 2. Paxos 算法 4. Gossip 協議 5. 分佈式通用設計 6. 一致性 Hash(補充)

📚📚👉👉👉本站這篇博客: https://segmentfault.com/a/1190000047292855 中查看
📚📚👉👉👉本站這篇博客: https://segmentfault.com/a/1190000047292855 中查看
<!-- end:bj1 -->
✨ 本教程項目亮點
🧠 知識體系完整:覆蓋從基礎原理、核心方法到高階應用的全流程內容
💻 全技術鏈覆蓋:完整前後端技術棧,涵蓋開發必備技能
🚀 從零到實戰:適合 0 基礎入門到提升,循序漸進掌握核心能力
📚 豐富文檔與代碼示例:涵蓋多種場景,可運行、可複用
🛠 工作與學習雙參考:不僅適合系統化學習,更可作為日常開發中的查閲手冊
🧩 模塊化知識結構:按知識點分章節,便於快速定位和複習
📈 長期可用的技術積累:不止一次學習,而是能伴隨工作與項目長期參考
🎯🎯🎯全教程總章節
🚀🚀🚀本篇主要內容
4. 索引
要求
- 瞭解常見索引與它們的適用場景,尤其是 B+Tree 索引的特點
- 掌握索引用於排序,以及失效情況
- 掌握索引用於篩選,以及失效情況
- 理解索引條件下推
- 理解二級索引覆蓋
索引基礎
常見索引
-
哈希索引
- 理想時間複雜度為 $O(1)$
- 適用場景:適用於等值查詢的場景,內存數據的索引
- 典型實現:Redis,MySQL 的 memory 引擎
-
平衡二叉樹索引
- 查詢和更新的時間複雜度都是 $O(log_2(n))$
- 適用場景:適用於等值查詢以及範圍查詢;適合內存數據的索引,但不適合磁盤數據的索引,可以認為樹的高度決定了磁盤 I/O 的次數,百萬數據樹高約為 20
-
BTree 索引
- BTree 其實就是 n 叉樹,分叉多意味着節點中的孩子(key)多,樹高自然就降低了
-
分叉數由頁大小和行(包括 key 與 value)大小決定
- 假設頁大小為 16k,每行 40 個字節,那麼分叉數就為 16k / 40 ≈ 410
- 而分叉為 410,則百萬數據樹高約為3,僅 3 次 I/O 就能找到所需數據
- 局部性原理:每次 I/O 按頁為單位讀取數據,把多個 key 相鄰的行放在同一頁中(每頁就是樹上一個節點),能進一步減少 I/O
-
B+ 樹索引
- 在 BTree 的基礎上做了改進,索引上只存儲 key,這樣能進一步增加分叉數,假設 key 佔 13 個字節,那麼一頁數據分叉數可以到 1260,樹高可以進一步下降為 2
樹高計算公式
- $log_{10}(N) / log_{10}(M)$ 其中 N 為數據行數,M 為分叉數
BTree vs B+Tree
- 無論 BTree 還是 B+Tree,每個葉子節點到根節點距離都相同
- BTree key 及 value 在每個節點上,無論葉子還是非葉子節點
<img src="/img/bVdmLgh" alt="image-20210901170943656" style="zoom:80%;" />
-
B+Tree 普通節點只存 key,葉子節點才存儲 key 和 value,因此分叉數可以更多
- 不過也請注意,普通節點上的 key 有的會與葉子節點的 key 重複
- B+Tree 必須到達葉子節點才能找到 value
- B+Tree 葉子節點用鏈表連接,可以方便範圍查詢及全表遍歷
<img src="/img/bVdmLgi" alt="image-20210901170954328" style="zoom:80%;" />
注:這兩張圖都是僅畫了 key,未畫 value
B+Tree 新增 key
假設階數(m)為5
-
若為空樹,那麼直接創建一個節點,插入 key 即可,此時這個葉子結點也是根結點。例如,插入 5
- 插入時,若當前結點 key 的個數小於階數,則插入結束
-
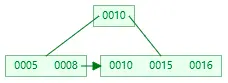
依次插入 8、10、15,按 key 大小升序
-
插入 16,這時到達了階數限制,所以要進行分裂
-
葉子節點分裂規則:將這個葉子結點分裂成左右兩個葉子結點,左葉子結點包含前 m/2 個(2個)記錄,右結點包含剩下的記錄,將中間的 key 進位到父結點中。注意:中間的 key 仍會保留在葉子節點一份
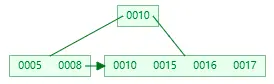
-
插入 17
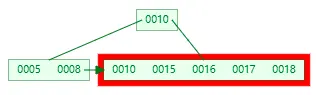
-
插入 18,這時當前結點的 key 個數到達 5,進行分裂
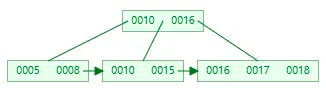
-
分裂成兩個結點,左結點 2 個記錄,右結點 3 個記錄,key 16 進位到父結點中
-
插入 19、20、21、22、6、9
-
插入 7,當前結點的 key 個數到達 5,需要分裂
-
分裂後 key 7 進入到父結點中,這時父節點 key 個數也到達 5
-
非葉子節點分裂規則:左子結點包含前 (m-1)/2 個 key,將中間的 key 進位到父結點中(不保留),右子節點包含剩餘的 key
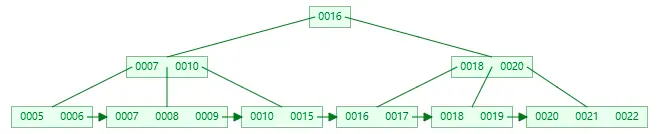
B+Tree 查詢 key
以查詢 15 為例
-
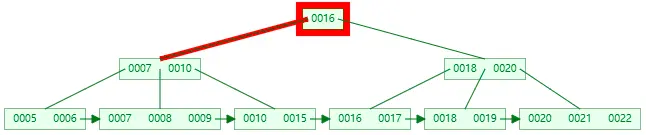
第一次 I/O
-
第二次 I/O
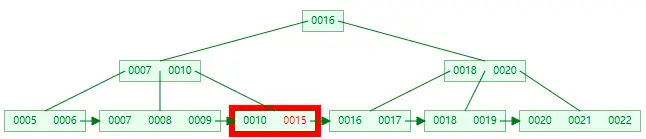
-
第三次 I/O
**B+Tree 刪除葉
🚀✨ (未完待續)項目系列下一章
📚下一篇 將進入更精彩的環節!
🔔 記得收藏 & 關注,第一時間獲取更新!
🍅 一起見證整個系列逐步成型的全過程。