二分查找的概念本身很容易理解,這裏不做贅述。其使用前提只有一個:單調數組
樸素二分查找
當在一個有向數組中,查找數組中是否有某個值,代碼很簡單:
const binarySearch = (nums, target) => {
let l = 0;
let r = nums.length - 1;
while(l<=r) {
const mid = (l+r) >> 1
if(nums[mid]<target) {
l = mid + 1
} else if(nums[mid]>target) {
r = mid - 1
} else {
return mid
}
}
return -1
};各類變種題及解題模板
實際使用時,用到樸素二分查找的情況反而更少,例如將4插入數組[1,2,2,3,3,4,4,5]中,插入後的數組保持單調遞增,我們需要先找到小於4的邊界(3的索引),再將4插入到這個邊界後面。
如何理解這個查找過程
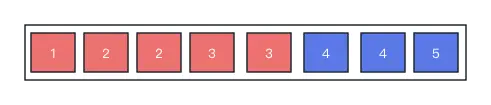
首先將數組看作如圖所示紅藍兩個區域,紅區代表所有小於target的值,藍區代表所有不小於target的值。那麼應該如何找到紅區和藍區的邊界?
解題模板
模板如下:
// 通用模板
const binarySearch = (arr, isLeftPart) => {
// 邊界處理
if(!isLeftPart(arr[0])) return [-1, 0];
if(isLeftPart(arr[arr.length - 1])) return [arr.length-1, arr.length];
let l = 0;
let r = arr.length - 1;
// 注意,條件是l<r-1
while(l<r-1) {
const mid = (l+r)>>1;
// 説明mid處於紅區,需要給l賦值mid
if(isLeftPart(arr[mid])) {
l = mid
} else {
r = mid
}
}
return [l, r];
}
// 測試代碼
const arr = [1,2,2,3,3,4,4,5];
const [_, idx] = binarySearch(arr, (val)=>val<4);
// insert
arr.splice(idx, 0, 4);
console.log(arr)通用模板返回結構[l, r],l代表紅區的右邊界,r代表藍區的左邊界。
無論如何變化,這類變種題最後要找的一般就是l或者r。
while的邊界問題
樸素二分查找中,while條件是while(l<=r),而解題模板中則是while(l<r-1),這種邊界是如何區分的?
我們需要明白,while代表終止條件,第一個不滿足條件的情況即為終止時的狀態。
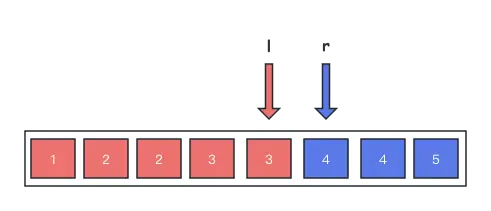
以通用模板為例,終止時l和r的指向應如圖所示:
可以看到,這個終止態時,l === r-1,那麼非終止態,也就是while循環條件應當是while(l<r-1).
同理,對於樸素二分查找,l===r時,仍要判斷該值是否是查找值,只有當l>r才能斷定查找完畢,因此while條件是while(l<=r)。