前言

解決問題思維方式

假設我們有一整套螺絲刀，要進行筆記本清灰操作，我們主要的思維邏輯如下：

1. 若要清灰，必須先取出風扇
2. 若要取出風扇，必須先把從外殼到風扇的螺絲全部拆下

那麼清灰問題就變成了拆一堆不同規格的螺絲，當我們看到不同規格的螺絲，就會比較螺絲口大小、形狀和螺絲刀規格，從而選取對應的螺絲刀。

可以看出，當我們遇到一個複雜問題，下意識的思維方式就是將一個複雜問題，轉移成我們熟知的一些子問題

問題模型的遍歷

選擇對應螺絲刀的過程，也有不同的選擇方式：

• 較笨的方式：每遇到一個螺絲，遍歷每個螺絲刀，選擇合適的螺絲刀
• 更好的方式：將螺絲刀分類（一字頭，十字頭），遇到對應的螺絲口（如十字頭），遍歷對應的（十字頭）螺絲刀，選擇合適的螺絲刀
• 熟練工的選擇方式：熟練工甚至記住了每個螺絲口對應的螺絲刀，看到螺絲口就能立馬反應出應該使用哪個螺絲刀

可以看出，當我們遇到一個問題時，會遍歷腦中的工具箱去尋找合適的解決工具，先將工具分類，遇到對應的問題時，可以根據問題特徵快速找到對應分類，從而搜索對應的工具。

當熟練度更高時，我們能更細化的瞭解每個工具的特徵，遇到對應的細節，能更快反應去用哪種工具解決問題。

小結

為了解決一個複雜問題，我們的總體思路如下（和在網絡上與人對線思路一致）：

1. 將問題簡化成我們所熟知的多個子問題（將對方智商拉到和自己一個水平）
2. 用現有的工具去匹配這些子問題，並加以解決（利用自己豐富的經驗打敗對方）

瞭解到這個過程後，為了具備解決更多問題的能力，我們所要豐富的知識主要有兩方面：

1. 熟悉更多的問題模型（雙指針、樹、圖....）
2. 掌握更多解決問題的工具（二分查找、深度/廣度優先遍歷、滑動窗口、dp...）

排序

學排序首先都是從冒泡排序開始，冒泡排序的寫法自不必説，眾所周知，冒泡的複雜度是O(n^2)，若細分這n*n的複雜度，可以發現每次獲取最大值需要比較n次，並且一共需要進行n次這樣的最大值比較。

我們知道一個合格的排序算法，複雜度應該是O(nlogn)，那麼這logn的優化，應該可能來源於兩方面：

1. 獲取最大值的比較時，只需要比較logn次
2. 一共只需要進行logn次這樣的獲取最大值的比較

因為我們已經知道這些排序算法複雜度是O(nlogn)，這也就意味着兩種優化不可能同時進行，否則排序算法的複雜度是O((logn)^2)了。

現在，我們將排序算法的優化問題，轉換成兩個稍微簡單點的問題了：

1. 如何在logn的複雜度下，獲取數組的最大值
2. 如果只進行logn次獲取最大值的比較

接下來，需要尋找或者學習某樣工具，來讓我們知道解決方案

二分查找

見文檔二分查找及各類變種題模板

通過二分查找這個工具的學習，我們知道了存在logn的複雜度下，獲取有向數組某個值的方法，那麼如何得到有向數組呢？我們很容易想到插入排序。

插入排序會始終維護一個有向數組，那麼將這個有向數組，結合二分查找，便能得到一個O(nlogn)複雜度的算法。

樹結構的應用

分治法

分治法在日常生活和工作中經常會用到，公司高管不會和基層員工直接對接，我們平時面對複雜業務需求時，也習慣將一個複雜需求分解成多個更為簡單的子需求。

分治的效果是，公司的CEO只用聽幾個高管的彙報，項目管理只需要監督幾個主要需求的進度，更多細節由下一層的管理者/需求進行同樣的管理操作，作為一個完成最小任務的員工，我們明顯能感覺到，相較於一個大的複雜業務，逐個解決最小任務明顯心智負擔更小，事實上這麼拆分任務，確實也常常能在更短工期內將任務解決。

排序中分治法最典型的應用是歸併排序，其代碼很簡單：

function mergeSort(ar) {
  const combine = (arr, l, half, r) => {
    const lArr = arr.slice(l, half + 1).concat(Infinity); // 哨兵
    const rArr = arr.slice(half + 1, r + 1).concat(Infinity);
    for (let i = l, lp = 0, rp = 0; i <= r; i++) {
      arr[i] = lArr[lp] <= rArr[rp] ? lArr[lp++] : rArr[rp++];
    }
  };
  const splitCombine = (arr, l, r) => {
    if (l >= r) return;
    const half = Math.floor((l + r) / 2);
    splitCombine(arr, l, half);
    splitCombine(arr, half + 1, r);
    combine(arr, l, half, r);
  };
  splitCombine(ar, 0, ar.length - 1);
  return ar;
}

歸併排序代碼邏輯暫時不做贅述，網上相關內容很多，這裏需要明確一個問題：分治降低了問題的複雜度，具體是降低了哪個方面的複雜度？

先從分析歸併排序複雜度入手，可以發現：

• 每一次合併，複雜度仍是O(n)
• 二分法進行數組拆分，總合並次數為O(logn)

之前提到，排序的優化可以從兩方面入手（每次比較大複雜度，比較次數），和結合了二分查找的插入排序不同，歸併排序的優化體現在比較次數上。

結合了二分查找的插入排序能優化每次比較大複雜度，這個很好理解，但為什麼分治法能減少比較次數？

這個主要體現在兩方面：

1. 子問題規模的減小

   • 問題的複雜度往往是隨着規模增大，而呈現指數型的增長，以解決複雜問題為例：一個複雜中假設有n個全局變量，我們調整某個全局變量的值時，往往需要考慮到這n個全局變量，但如果理清了業務邏輯，將複雜任務拆分成多個子任務，調整一個全局變量後，只需要考慮這個變量對於其父節點的影響，需要考慮的變量數量就變成了logn

2. 避免重複計算

   • 回到歸併排序，歸併排序的combine操作需要將兩個有序的子數組合併成一個更大的有序數組，注意這裏子數組也是有序的，這一次合併時，無需再重新對子數組進行排序，這就相當於遞進式的完成任務，上一次的工作能為這一次的工作節省時間，而冒泡排序中，上一次最大值的比較對下一次比較基本沒有太大幫助，每次比較都需要重複計算一部分內容

回頭看我們在工作中，將一個複雜任務拆分成多個子模塊，子模塊再進一步進行拆分，其實最後在完成項目時，代碼量並不會減少，但每一項子任務的複雜度都降低了，複雜度降低同時也意味着維護成本低降低，每次定位問題就像是在二叉搜索樹中查找某個值一樣，相較於屎山，複雜度直接從O(n)降低到O(logn)

同樣採用了分治法的還有快速排序，快排的代碼和複雜度分析這裏也不做贅述，直接總結它的特點：

1. 其平均複雜度為O(nlogn)，但最壞情況複雜度為O(n^2)
2. 歸併、優化後的插排都需要開闢額外內存空間，快排是原地交換，無需開闢額外內存

將數組當作樹來用

這裏章節其實有點不好劃分，因為二分查找本質上也是將數組當作樹來用（類似於二叉搜索樹），但平時我們使用二分法時，更多是用數組的方式去理解，所以這裏將它和數組當作樹的方法區分開來。

對於二叉搜索樹來説，找到某個值只需要log(n)，因為我們可以根據查找值和節點值的大小，判斷下一步應該從節點左側還是右側查找，那麼這個特性如果用在數組中，是否也能達到將算法優化到O(nlogn)的效果？

首先分析一下數組排序這件事，排序不涉及到數組長度的變化，且由於數組的特性，我們可以在O(1)時間內找到數組中的第n項，結合完全二叉樹的特性，如果給節點進行編號，我們可以輕鬆的知道編號n的節點，其左節點編號為2*n+1，如果將數組構建成一個平衡二叉樹（不是真的將數組轉換成樹，而是根據index在邏輯上將數組當作樹），那麼我們就能在O(logn)的時間內找到數組中的某個值。

這種方式用於數組排序就是堆排序，其思路如下：

1. 構建大頂堆（根節點永遠比左右節點大）
2. 將最大值和隊尾數字交換，再重新構建大頂堆，再次構建時，我們可以清楚知道頂部節點是和左節點交換還是右節點交換，因此只需O(logn)次交換

代碼如下：

/**
 * 共分為三部：
 * 1. 創建大頂堆
 * 2. 頂部和尾部換位置，縮小heapSize, 重複大頂堆化
 * 3. heapSize縮小至0即全部排序完畢
 * @param {Array} arr 
 * @returns arr
 */
function heapSort(arr) {
  let heapSize = arr.length - 1;
  const swap = (ar, i, j) =>{[ar[i], ar[j]] = [ar[j], ar[i]]};
  const maxHeapify = (ar, i) => {
    const left = 2*i + 1;
    const right = 2*i + 2;
    let largest = i;
    if(left<= heapSize && ar[left]>ar[largest]) {
      largest = left
    }
    if(right<=heapSize && ar[right]>ar[largest]) {
      largest = right
    }
    if(largest!==i) {
      swap(ar, i, largest)
      maxHeapify(ar, largest)
    }
  }
  const buildMaxHeap = (ar)=>{
    for(let i=~~((ar.length-1)/2);i>=0;i--) {
      maxHeapify(ar, i)
    }
  }
  buildMaxHeap(arr);
  while(heapSize>0) {
    swap(arr, 0, heapSize);
    heapSize--
    maxHeapify(arr, 0)
  }
  return arr
}

由於堆排序是一次次尋找第n大的元素，因此遇到數組中第n大元素這類題目時，能更快得到答案，同時堆排序也是原地替換，空間複雜度低。

排序相關內容小結

1. 優化方向

   • 減少每次獲取最大值時大複雜度
   • 減少比較次數

2. 優化思路

   • 分治（歸併）
   • 結合樹結構（二分查找、堆排）

3. 啓發

   • 工作中遇到複雜問題時，採用分治法將其分解成多個子任務，能有效降低複雜度

4. 獲得技能

   • 二分查找
   • 關鍵字"數組中第n大"這類問題的解決方案（堆排序，其實快排也能解決這類問題，不過快排寫起來容易出錯，有興趣看網上相關資料）

樹與圖

抽象認知

樹相關的問題其實如果遞歸理解得好，無論是各種遍歷，還是剪枝、回溯等操作，實現起來都很簡單。

圖相對於樹而言，最大的區別就是存在環，如果直接遍歷，很容易在環中鬼打牆，現實中走迷宮時，我們都知道在走過的路線上做標記（記住走過路線的特徵也是在腦中做標記），避免重複繞圈，圖也是一樣，如果將走過的路線存起來，每次選擇下一條路線時，只選擇沒走過的路線，就能避免鬼打牆的情況。

因此解決樹和圖的問題之前，我們先要學會兩件事：

1. 解決暈遞歸
2. 學會緩存法

暈遞歸問題

這裏先不做經驗性的總結，感性認知雖然更容易接受，但遇到更復雜的情況，比如雙遞歸，或者是在工作中遇到實現webpack插件、eslint插件的需求時，有時需要操作AST樹的節點，複雜情況甚至需要操作n重的環形引用（A方法引用方法B，B引用C，C又引用A），這時如果僅僅是對遞歸有感性認知，很容易出錯或者出現死循環。

首先我們需要知道遞歸是什麼。

遞歸是站在人的角度上解釋代碼，電腦只知道帶着怎麼樣的上下文，跳到哪一行代碼，其本質上也是一種循環。可以參考youtube上這個視頻（作者PPT地址），視頻講述瞭如何採用模擬棧的方式，將單遞歸和尾遞歸轉換成循環的寫法，編譯器用模擬棧的方式，將人理解的遞歸轉換成機器可以理解的循環。

循環和遞歸其實有些像用初中高中的數學知識和用線性代數解方程，對於二元一次方程，往往用初高中的數學解法更為容易，但當問題變成m元n次方程，就必須借用線性代數相關知識，但本質上初高中數學的解法也能用線性代數去解釋。

言歸正傳，我們用while循環類比遞歸，常規while循環結構如下：

while(循環條件) {
  問題的降解
}

while循環需包括兩個部分：

1. 每次執行while都是一步將問題降解的過程
2. 擁有跳出循環的條件，否則將變成死循環

這兩個特徵套用在遞歸中，遞歸的模板應該如下：

function recursion(n) {
  if(不滿足條件) return;
  問題的降解
  recursion(n-1); // 降解後的遞歸，這裏n-1是為了讓下一次遞歸知道問題的規模已經縮小，類似於for循環中的i
}

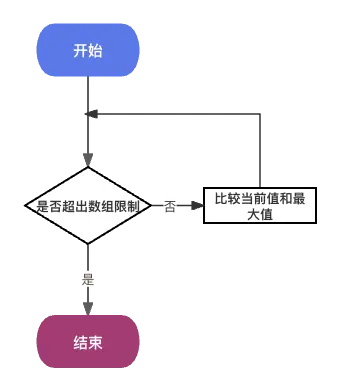
知道通用模板之後，我們應該怎麼去分析問題？其實可以用流程圖輔助分析

const findMaxVal = (arr) => {
    let max;
    const findMaxValInnerFunc = (idx) => {
        // 檢查是否超出限制，是則返回max
        if(idx>=arr.length) return max;
        // 比較當前值和最大值
        max = Math.max(arr[idx], max||0);
        // 進入下一次比較
        return findMaxValInnerFunc(idx+1)
    }
    return findMaxValInnerFunc(0)
}
console.log(findMaxVal([1,2,3,4,8,2,1])) // 8

畫好流程圖後，很容易實現一一對應的遞歸代碼，當面對複雜問題時，先畫流程圖，再按照流程圖進行代碼實現或許是個不錯的方式。

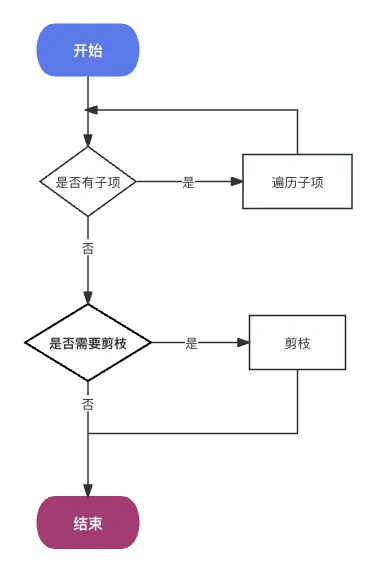
同樣的流程,嘗試一下樹的剪枝操作,我們將對象看作樹，需要剪除對象{a: 1, b: {c: null, d: {e: undefined}, f: undefined}}對象上，所有值為undefined、null或者空對象{}的節點，剪枝後的對象應為{a: 1}(這裏b被整個剪除，因為其所有子節點都被剪除了)，流程圖如下：

const prune = (obj) => {
    const isObj = (val) => Object.prototype.toString.call(val) === '[object Object]';
    const needToPrune = (val) =>  [null, undefined].includes(val) || (isObj(val) && !Object.keys(val).length);
    // 邊界處理
    if(!isObj(obj)) return obj;
    // 此處開始，按照流程圖操作
    const pruneFunc = (key, pNode) => {
        const val = pNode[key];
        // 是否有子項
        if(isObj(val)) {
            // 遍歷子項
            Object.keys(val).forEach(k=>pruneFunc(k, val))
        }
        if(needToPrune(val)) {
            // 對於滿足條件的項進行剪枝
            delete pNode[key]
        }
    }
    // 封裝傳入對象，使其符合函數參數定義
    pruneFunc("root",{root: obj});
    return obj
}
console.log(prune({a: 1, b: {c: null, d: {e: undefined}, f: undefined}}))

之前的項目中有用同樣的方式，梳理函數引用是否形成環的判斷邏輯（見：eslint內存泄漏排查工具開發）

樹的回溯（遞歸概念的練習）

我們知道了遞歸過程中模擬棧的概念（對應的就是前端的閉包），它保證了函數體中的變量都有獨立的內存空間存儲，那麼函數外的變量呢？如果外部定義了一個數組，執行遞歸函數時會往這個數組中push了一個值，必然會對下一次遞歸調用產生影響，這就是回溯操作利用的特性。

直接上n叉樹的回溯的通用模板：

const visitCallback = (node, parentPath) => {
     // do someting...
}
const traverse = (root, visit) => {
    const path = []

    const traverseNode = (node) => {
        visit(node, path);
        path.push(node); // 重點
        (node?.children??[]).forEach(traverseNode)
        path.pop(); // 重點
    }
    traverseNode(root)
}
traverse(node, visitCallback)

注意這裏的path.push(node)和path.pop(),這就像是給一個公司的人買奶茶，規定大家喝完之後將空杯放回原處，如果每個人都嚴格執行，那麼最後可以得到位置原封不動的空杯。

回溯的本質就是用一個遞歸外部的數據結構存放我們需要的變量，每次遞歸操作完成後將變量復原，就像買奶茶的例子一樣，每個人都喝到了奶茶，但大家都將空杯放回了原處，所以杯子位置不會有變化。

緩存法

前端需求開發過程中，如果沒開發維護過樹組件，或許很少用樹結構，但Object對象的各種操作肯定沒法避免，Object對象可以看作多叉樹，而循環引用的對象就是典型的圖結構。
前端八股文中無法避免的一題就是深拷貝，這裏不考慮日期、函數等特殊類型，僅貼一段普通對象深拷貝的代碼：

function cloneDeep(data) {
  const isReference = (val) => val instanceof Object;
  // 防止循環引用，利用weakMap緩存已拷貝的對象
  const cache = new WeakMap();
  const cloneData = (val) => {
    if (!isReference(val)) return val;
    if (cache.has(val)) return cache.get(val);
    // val類型未知，可能是class，因此根據constructor new一個對象
    const ref = new val.constructor();
    // 先將創建的ref放入cache，若先遞歸再放，會陷入無限遞歸
    cache.set(val, ref);
    // Object.getOwnPropertyDescriptors獲取val所有項，包括enumerable為false，以及原型鏈上自己定義的對象
    for (const key in Object.getOwnPropertyDescriptors(val)) {
      ref[key] = cloneData(val[key]);
    }
    return ref;
  };
  return cloneData(data);
}

為了防止循環引用，代碼中定義了一個cache，用於記錄已經複製過的對象，這裏需要注意的是，我們應該在執行下一次遞歸之前將複製過的對象放入cache，否則將陷入死循環。
利用同樣的思路，可以嘗試一下經典的迷宮問題。

緩存法與動態規劃

如果想在最短的時間內瞭解動態規劃，緩存法無疑是第一選擇

前面我們提到過，當遇到一個複雜問題時，可以通過將其分解成多個子問題，從而降低思維難度。那麼應該如何分解？

動態規劃本質上是思路的轉變。和高中學習數學歸納法類似，面對一個問題，思路變成了如果要解決這個問題，我需要證明什麼，這些需要證明的內容，就是這個問題的子問題。

以最經典的爬樓梯問題為例，正向思考往往比較複雜，如果反過來想，如果想跳到最後一級台階，那麼最後一次跳躍應該是從哪一級台階開始？不難得出只能從第n-1級和第n-2級開始跳，那麼我們可以得到最基礎的代碼：

var climbStairs = function(n) {
    // ...
    return climbStairs(n-1) + climbStairs(n-2)
};

但以遞歸的角度來看，這種寫法明顯是有問題的，根據我們前面總結的內容，遞歸需要包含兩項特點：

1. 每次執行都降解了問題的複雜度
2. 有跳出遞歸的判定

顯然這短代碼缺少了跳出遞歸的判斷，因此加上判定後，代碼如下：

var climbStairs = function(n) {
    if(n===1) return 1
    if(n===2) return 2
    return climbStairs(n-1) + climbStairs(n-2)
};

執行測試用例，可以發現這個函數已經可以得到正確結果了，但又會發現一個新的問題：當n的數值較大時，運算將變得特別慢。

這種多重遞歸，如果畫圖表示的話，可以發現它呈樹形展開，也就是複雜度會隨n的增加呈現指數增長。但仔細看會發現這些計算很多都是重複的，例如計算climbStairs(n-1) + climbStairs(n-2)時，計算climbStairs(n-1)必須先算climbStairs(n-2)，而後面又要再算一遍climbStairs(n-2)，那麼為什麼不直接將每次的計算結果緩存起來？

var climbStairs = function(n) {
    const cache = {};
    const calc = (m) => {
        if(m===1) return 1;
        if(m===2) return 2;
        if(m in cache) return cache[m];
        const result = calc(m-1) + calc(m-2);
        cache[m] = result;
        return result;
    }
    return calc(n);
};

當然，如果為了優化空間複雜度，也可以採用循環的方式，用兩個變量分別記錄第m、m+1級台階的結果，直至m==n，但緩存法作為動態規劃的入門更為直觀。

動態規劃的本質其實就和做項目一樣，將一個複雜問題轉換成多個子問題（解決暈遞歸問題後，這部分的代碼實現將會很簡單），再利用緩存法解決重複的計算過程，理清整個思路後，可以進一步用循環的方式優化空間複雜度。

樹與圖相關知識點小結

獲得技能

1. 暈遞歸的輔助解決方案
2. 回溯操作
3. 緩存法和動態規劃的入門知識

啓發

1. 學會反向思考，遇到問題時，拆解子問題的思路變成了：為了解決這個問題，我需要解決哪幾個子問題
2. 前一章節我們知道了分治法可以降低問題的複雜度，這一章知道了遇到複雜問題，如何進行分治

工具的積累

前兩章內容解決了思路問題，後面需要掌握的是具體的工具，如滑動窗口、位運算、字典樹、單調棧......

後續將會陸續總結更新.