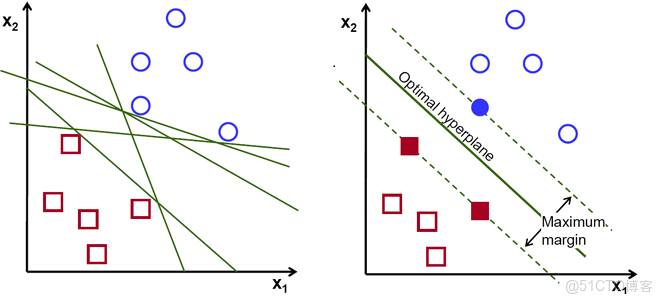
在過去二十餘年中，支持向量機（Support Vector Machine, SVM）一直是統計學習與模式識別領域的重要工具。其理論基礎源自結構風險最小化原則，結合幾何間隔最大化的優化目標，使得SVM在有限樣本條件下表現出優異的泛化能力。在文本分類、圖像識別、生物信息學等多種任務中，SVM憑藉穩健的訓練性質和嚴格的數學可解釋性，曾成為學術研究和工業應用的首選方法。

然而，隨着數據採集技術的進步和計算能力的增強，現代應用中常常面對數百萬乃至數十億的樣本，以及數十萬維甚至百萬維的特徵空間。這種環境對算法提出了新的挑戰：訓練時間、內存佔用和計算複雜度成為衡量算法可行性的關鍵因素。SVM的對偶問題依賴於核矩陣的構建與求解，而核矩陣的規模與樣本數量呈平方關係，使得傳統SVM在大規模數據場景下的訓練幾乎無法在常規硬件上完成。

一是SVM在大規模數據條件下的適用性如何科學評估；二是“大規模數據”應如何量化，從樣本數、特徵維度以及稀疏性等維度來看，何種規模才會對SVM訓練產生實質性影響。理解這些問題不僅關係到算法選擇，也涉及統計學習理論、優化算法與計算架構的深層聯繫。

1. SVM的理論框架與核心思想

支持向量機（SVM）的基本目標，是在特徵空間中尋找一個最優超平面，將不同類別的樣本儘可能準確地區分開，同時最大化類別間的間隔。對於線性可分問題，其優化目標可以形式化為：

約束條件為：

其中，表示第個樣本特徵，表示樣本類別標籤，為超平面法向量，為偏置項。該優化問題旨在尋找間隔最大的超平面，即最大化最小距離支持向量到超平面的間隔。

為了便於求解，該問題通常通過拉格朗日對偶方法轉化為對偶形式：

約束條件為：

其中為拉格朗日乘子，為軟間隔懲罰參數，為核函數。對偶形式的核心優勢在於可以通過核技巧處理非線性可分問題，將低維非線性邊界映射到高維線性可分空間，而無需顯式計算高維特徵。

常用核函數包括：

1. 線性核：
2. 多項式核：，，為多項式階數
3. 高斯徑向基函數（RBF核）：

非線性SVM的訓練核心在於對偶問題的求解，其中核矩陣的存儲和計算複雜度直接影響算法在大數據條件下的可行性。具體而言，標準SVM的時間複雜度大致為，空間複雜度為，這意味着當樣本數量增大時，計算和內存需求呈指數級上升。

為了增強SVM的可擴展性，研究者提出了多種優化策略，包括線性SVM、核近似方法、分塊訓練和分佈式優化。這些方法通過降低對核矩陣的依賴或採用隨機優化策略，使SVM在樣本量大時仍能保持合理的訓練效率。

2. “大規模數據”的度量標準

“大規模數據”是一個相對概念，其定義取決於算法在給定計算資源下的可處理能力。對於SVM而言，可以從以下幾個維度進行量化：

2.1 樣本數量（）

樣本數量是最直觀的衡量指標。對於非線性SVM，每個樣本都會生成對偶問題中的一個拉格朗日乘子，並參與核矩陣計算。由於核矩陣規模為，存儲需求為，計算需求為。

例如，若，則核矩陣約有個元素，假設每個元素佔8字節內存，則單機內存需求約為80GB，超出大多數常規工作站的容量。此時，傳統非線性SVM訓練幾乎不可執行，必須考慮核近似或分佈式計算策略。

2.2 特徵維度（）

特徵維度影響線性SVM的訓練效率。線性SVM優化問題可寫為：

對於稀疏高維數據，梯度計算複雜度為。當非常大時，即使線性SVM也可能出現訓練時間長或收斂緩慢的問題，但通過稀疏矩陣存儲和隨機梯度下降（SGD）優化，可以在合理時間內完成訓練。

2.3 數據稀疏性

稀疏數據可顯著降低存儲和計算開銷。文本分類中的TF-IDF向量通常是高維稀疏向量，線性SVM在這種條件下能夠高效處理。非線性核方法通常會破壞稀疏性，使計算和存儲負擔重建到密集矩陣級別，這也是大規模數據下核SVM受限的原因之一。

2.4 計算資源

“大規模”還取決於可用硬件資源，包括CPU/GPU數量、內存容量和分佈式計算能力。對於同一算法，單機可處理樣本數可能為~，而通過分佈式訓練或GPU加速，可擴展到甚至樣本級別。

2.5 綜合判斷標準

綜上，可以將“大規模數據”定義為：當樣本數達到級或更高，特徵維度高於，且核矩陣無法在常規單機內存中存儲時，SVM訓練受到顯著限制。在這種條件下，需要採用線性SVM、核近似或分佈式優化方法，以保持訓練的可行性和效率。

3. 計算複雜度分析

3.1 理論複雜度

標準SVM的訓練過程通常需要求解一個二次規劃（Quadratic Programming, QP）問題。若採用傳統的QP求解器，其時間複雜度為，空間複雜度為。

以樣本數為例，核矩陣的大小約為個元素，即約需80GB內存（以雙精度存儲計），顯然超出單機計算能力。因此，SVM的標準求解在大樣本條件下並不現實。

3.2 核函數計算負擔

在非線性SVM中，每次迭代都需計算核函數。常見核函數包括：

• 線性核：
• 多項式核：
• RBF核：

其中，RBF核計算量最大，因為它要求計算每對樣本的歐氏距離。當樣本量增大時，核計算成為主要瓶頸。

4. SVM在大規模數據下的優化策略

雖然傳統SVM不適用於大數據，但研究者提出了多種改進方案，試圖在保證泛化性能的同時降低計算負擔。

4.1 線性SVM（Linear SVM）

當數據在高維空間中近似線性可分時，線性SVM成為首選。其目標函數簡化為：

利用隨機梯度下降（SGD）或Pegasos算法，訓練複雜度可降至，並可通過批量優化、並行化顯著加速。這類算法能處理上億樣本的任務，常用於文本與廣告分類。

4.2 分塊訓練與SMO算法

Sequential Minimal Optimization (SMO)是SVM的核心優化算法之一。其思想是將大規模二次規劃分解為一系列兩個變量的小問題，從而避免矩陣求逆運算。SMO的時間複雜度在實踐中通常介於到之間。

儘管SMO顯著提高了效率，但當過大時，每次迭代仍需掃描全部樣本，收斂速度變慢。因此，對於百萬級數據，仍需進一步的分佈式或近似方案。

4.3 核近似方法

為了避免直接計算核矩陣，可使用核近似技術。典型方法包括：

• Nystrom方法：從訓練集中抽取個樣本（），構造近似核矩陣，複雜度降為。
• 隨機傅里葉特徵（Random Fourier Features, RFF）：通過將RBF核映射為顯式特徵空間，使SVM退化為線性形式，訓練複雜度降為，其中為映射維度。

這兩種方法在保留部分非線性能力的同時，大幅提升了可擴展性。

5. 分佈式與並行SVM

面對超大規模數據集，單機SVM的性能終究受限。為此，研究者提出了多種分佈式訓練架構。

5.1 MapReduce與分佈式分塊

Hadoop或Spark框架下的SVM實現將訓練數據分割為多個子集，每個子集獨立訓練局部SVM，隨後通過模型融合（如多數投票或模型平均）獲得全局分類器。這種策略近似於分佈式Bagging，但會帶來模型一致性問題。

5.2 參數服務器架構

參數服務器（Parameter Server）框架可支持分佈式梯度同步，使得線性SVM和核近似SVM都能在數十台機器上協同訓練。這種方式能在億級樣本下實現穩定收斂。

5.3 GPU加速

GPU擅長並行矩陣運算，適合SVM核計算任務。尤其在RBF核下，通過CUDA實現的核矩陣計算可獲得數十倍加速。但GPU顯存有限，因此通常結合核近似或分批計算策略使用。

6. 泛化性能與模型穩定性

在採用近似、分塊或線性化之後，SVM的泛化能力是否會顯著下降？

理論上，SVM的泛化性能依賴於結構風險最小化原則，其界為：

其中為VC維。可見，當樣本數增大時，泛化誤差界下降；但若近似過度，實際分類間隔縮小，則增大。

因此，線性化或核近似SVM的關鍵在於維持良好的間隔與表示能力之間的平衡。經驗研究表明，RFF與Nystrom方法在特徵映射維度適當時，其精度可接近全核SVM，但訓練時間縮短兩個數量級。

7. 與其他算法的比較

7.1 與深度學習的比較

深度學習在大規模數據上表現優越，原因在於其優化目標可通過小批量梯度下降實現，並具有強大的特徵學習能力。而SVM則依賴核函數人工設計。

但在樣本量較小或特徵高度稀疏時，SVM依然具有優勢，因為其目標函數凸，訓練穩定且不易陷入局部極值。

7.2 與樹模型的比較

梯度提升樹（GBDT、XGBoost等）在大數據任務中表現出高效性，尤其在非線性關係建模上更靈活。SVM在同樣規模下往往因核計算開銷過大而不具競爭力。

然而，樹模型缺乏SVM在理論上的嚴格泛化界，因此在需要嚴格數學保證的任務中，SVM仍具學術價值。

8. 工程實踐視角

從工程實現角度看，SVM是否適合大規模數據，取決於以下因素的綜合權衡：

• 數據規模與硬件資源匹配性
• 任務的線性可分程度
• 核函數的選取
• 容忍的訓練時間與精度損失

例如，在搜索引擎廣告點擊預測中，樣本量可達數十億條，此時線性SVM（如LIBLINEAR）仍被廣泛使用；而在蛋白質結構預測等任務中，樣本數相對較小但關係複雜，RBF核SVM仍為主流。

9. 理論層面的進一步探討

9.1 樣本複雜度與容量控制

當樣本數量遠超模型複雜度時，SVM的結構風險最小化原理能有效防止過擬合。但若特徵空間通過核映射擴展至無限維，模型容量迅速增大，需要通過正則化參數精細調節。

9.2 優化問題的可解性

在大數據條件下，即便SVM的優化問題在理論上是凸的，實際求解依舊面臨數值穩定性與內存限制問題。例如，拉格朗日乘子的數量與樣本等同，求解難以並行化。這也是核SVM在工程落地中的主要障礙。

10. 結論

支持向量機在理論上仍是分類與迴歸任務中極具代表性的算法，其幾何解釋與泛化理論具有長遠價值。然而，從計算複雜度與資源消耗角度看，SVM並非天然適合大規模數據。

在大數據條件下，SVM的適用性取決於是否採用線性形式、是否進行核近似、是否具備分佈式計算能力。若樣本數超過且採用非線性核，標準SVM將難以在合理時間內訓練完畢；若樣本量極大但線性可分，線性SVM仍然是高效可靠的選擇。

因此，可以將SVM對大規模數據的適應性歸納為：

• 核SVM：適合中小規模、高維、複雜邊界任務；
• 線性SVM：適合超大規模、稀疏特徵任務；
• 核近似SVM：適合中大型任務的平衡方案。

SVM的未來價值，或許不在取代深度學習，而在於提供一種理論上可解釋、計算上可調控的學習機制，為理解泛化與優化的數學規律提供堅實基礎。