集成學習系列：

• Blending and Bagging
• Adaptive Boosting
• Decision Tree
• Random Forest
• Gradient Boosted Decision Tree

Random Forest

1 - Random Forest Algorithm

這篇主要講述機器學習中的隨機森林算法相關的知識。首先回顧一下我們在前幾篇博文中提到的兩個模型，Bagging Bagging 和Decision Tree Decision Tree 。

1.1 - 回顧bagging和decision tree

Bagging B a g g i n g 算法的主要過程是通過bootstrap b o o t s t r a p 機制從原始的資料D D 中得到不同的大小為N′ N ′ 的資料D~t D ~ t ，將這些資料餵給base algorithm b a s e   a l g o r i t h m ，這裏記作算法A A ，得到一個gt g t 。最後使用uniform u n i f o r m 的方式將這些gt g t 融合起來作為算法最後得到的模型G G 。

Bagging算法
For t=1,2,⋯,TFor t=1,2,⋯,T
1.request size N′ data D~t by bootstrapping with D 1. r e q u e s t   s i z e   N ′   d a t a   D ~ t   b y   b o o t s t r a p p i n g   w i t h   D
2.obtain base gt by A(D~t) 2. o b t a i n   b a s e   g t   b y   A ( D ~ t )
return G=Uniform({gt}) r e t u r n   G = U n i f o r m ( { g t } )

Decision Tree D e c i s i o n   T r e e 算法通過遞歸的尋找一個在當前的資料上最好的劃分特徵或者説是分支條件b(x) b ( x ) ，來不斷的構建子樹，最終得到一個在不同的輸入下做不同的決策的G G 。

Decision Tree算法
function DTree(D)function DTree(D)
if termination i f   t e r m i n a t i o n
return base gt r e t u r n   b a s e   g t
else e l s e
1.learn b(x) and split D to Dc by b(x) 1. l e a r n   b ( x )   a n d   s p l i t   D   t o   D c   b y   b ( x )
2.build Gc⟵DTree(Dc) 2. b u i l d   G c ⟵ D T r e e ( D c )
3.return G(x)=∑Cc=1|[b(x)=c]|Gc(x) 3. r e t u r n   G ( x ) = ∑ c = 1 C | [ b ( x ) = c ] | G c ( x )

1.2 - 什麼是Random Forest（RF）

這兩個學習算法各自有一個很重要的特點：在Bagging Bagging 中， 如果底層的弱學習器沒有那麼穩定，也就是所謂的方差很大的時候（或者説是對數據比較敏感的時候），通過Bagging Bagging 中的uniform u n i f o r m 的方式，不管是投票還是平均，就會把這些variance v a r i a n c e 降低。巧的是decision tree decision tree 是一個對輸入的data d a t a 很敏感的算法，或者説這個算法的variance v a r i a n c e 很大， 可能data d a t a 變一點， 得到的樹就是不相同的。這兩個學習算法一個本身的variance v a r i a n c e 很大，一個可以降低variance v a r i a n c e 。我們就想如果合在一起是不是能夠取長補短呢？所以我們現在要做的事情就是用bagging b a g g i n g 的方式將一堆的decision tree d e c i s i o n   t r e e 融合起來，就得到了Random Forest R a n d o m   F o r e s t ，在上一篇的最後我們説這篇要介紹的是aggregation of aggregation a g g r e g a t i o n   o f   a g g r e g a t i o n 正是這個意思。

所以random forest r a n d o m   f o r e s t 中的random r a n d o m 描述的bagging b a g g i n g 算法中的bootstraping b o o t s t r a p i n g 所產生的隨機性，其中的forest f o r e s t 描述的事實是bagging b a g g i n g 的base learner b a s e   l e a r n e r 是decision tree d e c i s i o n   t r e e ，所以會產生很多的決策樹，很多樹合在一起就是森林forest f o r e s t 。

Bagging B a g g i n g 的base learner b a s e   l e a r n e r 是decision tree d e c i s i o n   t r e e 的算法就是random forest r a n d o m   f o r e s t 算法。

通過以上的分析Random Forest R a n d o m   F o r e s t 算法流程如下：只是將Bagging B a g g i n g 中的base alogrithm A b a s e   a l o g r i t h m   A 使用了decision tree d e c i s i o n   t r e e
Random Forest算法
For t=1,2,⋯,T F o r   t = 1 , 2 , ⋯ , T
1.request size N′ data D~t by bootstrapping with D 1. r e q u e s t   s i z e   N ′   d a t a   D ~ t   b y   b o o t s t r a p p i n g   w i t h   D
2.obtain base gt by DTree(D~t) 2. o b t a i n   b a s e   g t   b y   D T r e e ( D ~ t )
return G=Uniform({gt}) r e t u r n   G = U n i f o r m ( { g t } )

1.3 - RF的一些優點

這樣的算法其中的一個優點是所有decision tree d e c i s i o n   t r e e 的構建（從bagging b a g g i n g 算法中的bootstrap b o o t s t r a p 開始）可以 並行 的交給多個計算機去做，它們之間是互不影響。所以這個算法訓練的效率很高。另外CART算 C A R T 算 法中的很多優點：可以處理multi classification m u l t i   c l a s s i f i c a t i o n ，可以處理miss features m i s s   f e a t u r e s ， 可以處理categorical features c a t e g o r i c a l   f e a t u r e s ，這些好處都被隨機森立繼承了下來。而CART C A R T 算法中的主要缺點：對data d a t a 很敏感， 特別是對一棵完全長成的樹來説很容易過擬合，會因為bagging b a g g i n g 最後所做的uniform u n i f o r m 的關係而得到緩和。

1.4 - Random Forest中的一些技巧

在bagging b a g g i n g 中，為了得到不同的g g ， 我們進行的操作是通過boostrapboostrap對data d a t a 做隨機的抽取。還有另一種對數據抽取方法也可以幫助我們得到不同的g g ， 那就是抽取不同的特徵。例如在收集到的datadata中共有100個特徵， 我們每次隨機抽取其中的10個特徵來構造決策樹（在進行特徵選擇時候只考慮這10個特徵）。通過這樣的方式很明顯我們也能得到一些不一樣的決策樹。從技術上講就是從100個維度中抽取10個維度，相當於做了一個特徵轉換，或者是一個低維度的投影。同時這樣也使得算法更加的高效，原來decision tree d e c i s i o n   t r e e 中的decision stump d e c i s i o n   s t u m p 要在100個維度中挑選，現在只需要在10個維度中計算就好了。Random Forest R a n d o m   F o r e s t 的作者建議在每一次做分支branch b r a n c h 的時候，都可以做一次random r a n d o m 的sampling s a m p l i n g 來選擇不一樣的一些特徵進行子樹的構建，通過增加randomness r a n d o m n e s s 得到的樹可能就會更加的diversity d i v e r s i t y 。

實際的操作過程我想應該是：假設共有10個特徵，構造decision tree d e c i s i o n   t r e e 的時候，先隨機使用其中的4個特徵，假設是特徵1,4,5,7來選擇最好的用於劃分樹的方式，假設此時選擇到的特徵是5，那麼將數據集劃分話兩個（CART C A R T 算法的設置）子數據集；在其中的每一個子數據集再次隨機的選取所有的10個特徵中的4個特徵來進行子樹的構建，遞歸的執行直到結束。

或者我們可以考慮一種更加複雜的情況，在做分支branch b r a n c h 或者説選擇特徵劃分數據的時候，隨機的選擇n n 個特徵算它們的加權和然後以此為基礎劃分數據(randomly projected)(randomly projected)。這樣看來，RF R F 中的CART C A R T 算法如果採用random combination r a n d o m   c o m b i n a t i o n 構建特徵，並且使用decision stump d e c i s i o n   s t u m p 在構建的特徵上進行子樹的構建的話，其本質上很像是在使用perceptron p e r c e p t r o n 算法，即算一些特徵的加權和判斷和某一個閾值的關係進行分類。這樣的話我們就不僅僅可以得到”垂直”或者是”水平”的分割性，還可以得到”斜”的分割線。

這就是基本的random forest r a n d o m   f o r e s t 算法，可以看到除了在bagging b a g g i n g 中由bootstrap b o o t s t r a p 這樣的機制帶來的randomness r a n d o m n e s s 之外， 在CART C A R T 算法中每次決定分支branch b r a n c h 之前都要進行random combination r a n d o m   c o m b i n a t i o n 這樣的的操作，這樣就增添了更多的randomness r a n d o m n e s s 。

2 - Out-Of-Bag Estimate

2.1 - 重新認識下bootstrapping

剛剛我們介紹了Random Forest R a n d o m   F o r e s t ，其中的一個核心是bagging b a g g i n g ，bagging b a g g i n g 中利用了一個很重要的機制叫做bootstrap b o o t s t r a p ，利用這個機制可以從D D 中選擇出不同的樣本形成D~t D ~ t ，然後使用base learner b a s e   l e a r n e r 從D~t D ~ t 得到不同的gt g t 。
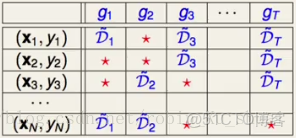
這個bootstrap b o o t s t r a p 的過程可以表示為如下的一個表格：

表一

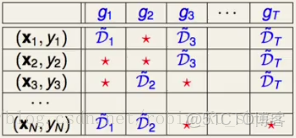
這個表格的第一列是所有的樣本{(x1,y1),(x2,y2),(x3,y3),⋯,(xN,yN)} { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , ⋯ , ( x N , y N ) } ， 表格的第二列表示的是：g1 g 1 是從D~1 D ~ 1 中學習得到的，在D~1 D ~ 1 中包括(x1,y1),(xN,yN) ( x 1 , y 1 ) , ( x N , y N ) 等， 但是不包括(x2,y2),(x3,y3) ( x 2 , y 2 ) , ( x 3 , y 3 ) 等，不包括的樣本使用★ ★ 表示。我們把這些沒有被選擇到的data d a t a ，也就是圖中是★ ★ 的數據稱為out o u t -of o f -bag(OOB) b a g ( O O B ) ， 這一小節主要開看看這些資料有什麼用處。更準確的説，(x2,y2),(x3,y3) ( x 2 , y 2 ) , ( x 3 , y 3 ) 稱為g1 g 1 的out o u t -of o f -bag b a g 。

2.2 - OOB的數量

我們先來計算一下，在bootstrapping b o o t s t r a p p i n g 的過程中有多少筆OOB O O B 的資料呢？假設我們從原來數量為N N 的資料DD中通過bootstrap b o o t s t r a p 的方式抽取N′ N ′ 筆資料。如果N′=N N ′ = N ，那麼樣本(xnyn) ( x n y n ) 在構造gt g t 的時候一次也沒有被抽到的可能性是：(1−1N)N ( 1 − 1 N ) N
如果N N 很大的時候：

(1−1N)N=1(NN−1)N=1(1+1N−1)N≈1e(1−1N)N=1(NN−1)N=1(1+1N−1)N≈1e

所以如果抽取N

N 次的話，大概有1e×N1e×N筆資料會沒有機會參與gt g t 的構建。也就是大概有三分之一的資料都是OOB O O B 的。

2.3 - 利用OOB的資料來做驗證

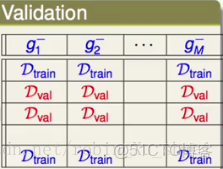
這些OOB O O B 的資料有什麼作用呢？首先我們看一張我們比較熟悉的關於Validation V a l i d a t i o n 的表格。

在做validation v a l i d a t i o n 的時候，我們將數據劃分為若干份，一部分用來做train t r a i n ， 一部分用來validation v a l i d a t i o n 。在上表的每一列中我們使用那些D~train D ~ t r a i n 來訓練得到不同的g−n g n − ，使用D~val D ~ v a l 衡量g−n g n − 的表現。D~val D ~ v a l 之所以可以衡量g−n g n − 的表現是因為D~val D ~ v a l 沒有參與g−n g n − 的構建。

那麼回到我們第一張表，其中被標記為★ ★ 的資料就相當於D~val D ~ v a l 。首先從數量上來説，我們通常validation v a l i d a t i o n 會使用五分之一或者是十分之一的資料， 剛剛我們推導了OOB O O B 的數量大概是三分之一。這樣的話， 這些OOB O O B 的資料就可以用來驗證gt g t 表現。但是在aggregation a g g r e g a t i o n 這系列的算法中，我們並不關心gt g t 的表現好不好，我們關心的是最終的G G 的表現。所以如果我們可以使用這些OOBOOB的資料來驗證G G 的好壞的話， 那麼我們就可以對GG做一些參數的選擇。

一種可行的方法如下：針對每一個樣本，我們看看在什麼時候這個樣本可以用做validation v a l i d a t i o n 的資料。例如對於表一中的最後一個樣本(xN,yN) ( x N , y N ) ，這個樣本可以當成g3 g 3 的validation v a l i d a t i o n 的資料，也可以當成是可以當成gT g T 的validation v a l i d a t i o n 的資料，因為(xN,yN) ( x N , y N ) 並沒有參與其中任意一個g g 的構建，所以(xN,yN)(xN,yN)可以當成是某個 G−N G N − 的validation v a l i d a t i o n 的資料，其中的G−N G N − 可以是bagging(g3,gT) b a g g i n g ( g 3 , g T ) ， 這樣我們就可以看看 G−N G N − 在 (xN,yN) ( x N , y N ) （將xN x N 帶入到G− G − 中看結果和yn y n 的差距）。那麼對於每一個樣本，我們都可以得到一個G−n G n − （其中n∈[1,N] n ∈ [ 1 , N ] ）來看看其在(xn,yn) ( x n , y n ) 上的表現如何。這就很像我們以前做validation v a l i d a t i o n 的時候提到的leave one out cross validation l e a v e   o n e   o u t   c r o s s   v a l i d a t i o n ：把每一筆資料都當做validation set v a l i d a t i o n   s e t ，來計算模型的表現如何最後做平均。所以通過這樣的方法我們可以定義很多G− G − 來大概的知道最終的G G 的表現如何。

利用OOBOOB來驗證G G 的表現：對於每一筆資料(xn,yn)(xn,yn)構建一個G− G − ，並計算G− G − 在該資料上的表現，最後對所有的資料做平均，計算公式如下：

Eoob(G)=1N∑n=1N err(yn,G−n(xn)) E o o b ( G ) = 1 N ∑ n = 1 N   e r r ( y n , G n − ( x n ) )

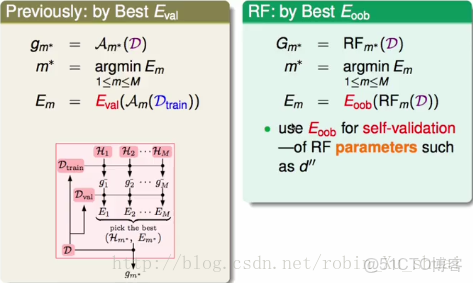
所以bagging b a g g i n g 或者是random forest r a n d o m   f o r e s t 算法就有這樣的優勢：在得到了一個G G 之後，我們就能計算出該GG好或者是不好。因為其中的bootstrap b o o t s t r a p 的過程使得這些算法可以做self validation s e l f   v a l i d a t i o n 。這樣就可以來對Bagging B a g g i n g 或者是Random Forest R a n d o m   F o r e s t 中的參數進行調優。

以前為了做模型的選擇需要將資料劃分為train set Dtrain t r a i n   s e t   D t r a i n 和validation set Dval v a l i d a t i o n   s e t   D v a l ，首先在Dtrain D t r a i n 上做訓練，然後在Dval D v a l 上驗證算法的好壞，通過不斷的選擇得到了好的模型之後還需要在D D 上再進行一次模型的訓練得到最終的結果。
現在有了OOB O O B 之後，不需要進行數據集的劃分，將所有的資料D D 都用於模型的訓練，然後使用EOOB E O O B 來進行模型的評估。

OOB O O B 的錯誤在實際應用中對於衡量G G 的表現來説通常相當的準確。

3 - Feature Selection

上一小節講述了OOBOOB可以用來衡量random forest r a n d o m   f o r e s t 的表現。這一節我們看看這樣的方法還可以用在什麼地方。我們這一小節關注一個新的問題：Feature Selection F e a t u r e   S e l e c t i o n 。 Feature Selection F e a t u r e   S e l e c t i o n 指的是當數據的維度很高的時候，我們可能想要把一些冗餘的或者沒有用的特徵移除掉，也可以認為是我們想要學到一個從高維度到低緯度的轉換， 通過這樣的方式來選擇好的特徵或者是輸入。 Feature Selection F e a t u r e   S e l e c t i o n 的好處有：會使得不管是訓練還是測試都更加的有效和簡單；刪除掉的維度可能是一些噪聲， 這樣能避免overfitting o v e r f i t t i n g 的發生。

Decision tree D e c i s i o n   t r e e 中需要選擇好的特徵來構建子樹（或者説選擇好的特徵做分支條件branch criteria b r a n c h   c r i t e r i a ），所以在這個模型中有自己的feature selection f e a t u r e   s e l e c t i o n 。在adaboost decision stump a d a b o o s t   d e c i s i o n   s t u m p 中也有做feature selection f e a t u r e   s e l e c t i o n 的過程。

我們做Feature Selection F e a t u r e   S e l e c t i o n 的主要思路是：不考慮特徵的交互關係，利用某種方法給每一個feature f e a t u r e 打一個分數來表示該feature f e a t u r e 的重要性。這樣排序之後取Top N T o p   N 得到的就是N N 個比較重要的featurefeature。

3.1 - 線性模型中的特徵選擇

這樣的想法在線性模型中特別容易實現，因為在最終的線性模型中我們使用每一個特徵和該特徵的權重w w 的乘積然後求和作為最後的得分，之後再將該分數應用到不同的問題當中，例如regressionregression或者是classifiction c l a s s i f i c t i o n 。所以當特徵x x 彼此之間取值的範圍差不多，並且ww還不錯的話，w w 的大小就是我們想要特徵featurefeature的重要性，所以使用w w 的大小當做featurefeature的重要性，經過排序取top N t o p   N 就能達到特徵選擇的效果。所以當做完一個linear model l i n e a r   m o d e l 之後，從模型返回的w w 中就可以得出每一個特徵的重要性，就可以完成一次特徵選擇。在特徵選擇之後，再決定是不是要利用這些特徵做第二階段或者是第三階段的線性的或者非線性的學習。

3.2 - 非線性模型中的特徵選擇

在非線性的模型中， 做特徵選擇通常就要困難很多，因為在非線性的模型中，特徵之間的關係是交雜在一起的，所以很難釐清單獨一個特徵的重要性。Random forestRandom forest雖然是一個非線性的模型，但是由於其中的一些機制，所以讓這個模型做特徵選擇相對來説比較簡單一些（這就是為什麼feature selection f e a t u r e   s e l e c t i o n 這個課題會選擇在這裏講的原因，因為是利用random forest r a n d o m   f o r e s t 的機制在做）。怎麼做呢？基本的方法叫做random test r a n d o m   t e s t ，該方法的思路是如果某一個特徵比較重要，那麼當這個特徵中被摻入了一些噪聲的時候，學習算法的表現一定會變差。所以通過比較學習的結果在原來的特徵下的表現和該特徵摻雜噪聲下的表現的差距，就能判斷這個特徵的重要性。

那麼摻雜一些什麼樣子的特徵呢？如果加一些常見的高斯分佈的噪聲，那麼可能會影響到這個特徵上原來取值的分佈。所以這可能不是一個很好的選擇。借鑑一下bootstrap b o o t s t r a p ，因為是在原始的資料中進行抽樣，所以這樣得到的結果在一定的程度上維持了原始的資料的分佈和特點。這裏我們採用另一種比較類似的機制：permutation p e r m u t a t i o n ，具體的做法是對所有樣本在該特徵下的取值做隨機的置換。這樣就產生了噪聲，並且保證了該特徵的分佈不會改變。這樣的做法在統計上稱為permutation test p e r m u t a t i o n   t e s t 。 所以衡量第 i i 個維度的特徵的重要性的公式如下：

importance(i)=performance(D)−performance(D(p))(1)(1)importance(i)=performance(D)−performance(D(p))

其中D

D 是原始的沒有permutation p e r m u t a t i o n 資料，D(p) D ( p ) 是將第 i i 個維度經過permutationpermutation的資料。

原始的random forest r a n d o m   f o r e s t 的作者建議可以使用permutation test p e r m u t a t i o n   t e s t 來計算每一個維度的重要性。這樣就可以拿來做特徵的選擇了。

根據(1) ( 1 ) 式，為了確定特徵 i i 的表現，看起來我們需要計算performance(D(p))performance(D(p))，那麼通常的做法是需要在數據D(p) D ( p ) 上重新訓練模型，使用validation v a l i d a t i o n 來驗證表現。但是因為我們使用的是random forest r a n d o m   f o r e s t ，可能不需要validation v a l i d a t i o n ，而使用Eoob E o o b 來代替就好了。那麼(1) ( 1 ) 式可以改為：

importance(i)=Eoob(G)−Eoob(G(p)) i m p o r t a n c e ( i ) = E o o b ( G ) − E o o b ( G ( p ) )

其中G G 是從DD得到的模型，G(p) G ( p ) 是從D(p) D ( p ) 得到的模型。G(p) G ( p ) 依然需要經過重新的訓練， 我們希望得到一個投機取巧的近似方式，省去再訓練一個模型G(p) G ( p ) 的時間。我們的做法是將Eoob(G(p)) E o o b ( G ( p ) ) 寫成 E(p)oob(G) E o o b ( p ) ( G ) ， 如果是這樣的話， 就不需要再訓練一個模型，而是仍然使用模型G G ， 只是在利用OOBOOB的資料做validation v a l i d a t i o n 的時候做手腳， 即在驗證的時候做permutation p e r m u t a t i o n ，而不是在訓練的時候做permutation p e r m u t a t i o n 。

具體的做法是：
假設我們現在感興趣的是第 i i 個特徵的重要性，在使用OOBOOB的資料(xn,yn) ( x n , y n ) 做leave one out validation l e a v e   o n e   o u t   v a l i d a t i o n 的時候，所有未使用該筆數據的gt g t 構成G− G − ，之前在計算EOOB E O O B 的時候直接計算G− G − 在(xn,yn) ( x n , y n ) 上的表現即可，即先計算每一個gt g t 在(xn,yn) ( x n , y n ) 上的得分，最後集成。但是現在有所不同， 在計算每一個gt g t 的時候，必然會用到第 xn,i x n , i ，這個時候就是我們可以做手腳的時候：針對(xn,yn) ( x n , y n ) 的輸入中的第i i 個特徵 xn,ixn,i 做 permutation p e r m u t a t i o n ，並且算法的作者要求使用對於G− G − 來説是OOB O O B 的資料來進行隨機的替換。對所有的樣本重複以上的工作，最後將Eoob E o o b 平均就得到了在對特徵 i i 做了permutationpermutation之後算法的表現。
使用這個的機制就可以得到每一個特徵的重要性，之後就可以做特徵的選擇。這個方法的核心工具是：

1. 利用OOB 機制。

在實際的應用當中，random forest r a n d o m   f o r e s t 的特徵選擇非常好用，很多人在面臨非線性的問題的時候，會先使用random forest r a n d o m   f o r e s t 來做一些初步的特徵選擇。

表一

4 - Random Forest算法的表現

4.1 - 資料1

一個簡單的數據資料
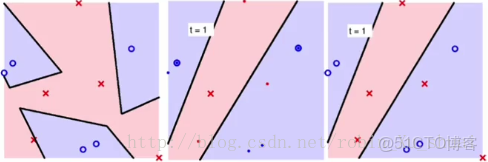
這一小節看一下random forest r a n d o m   f o r e s t 算法的表現，同樣針對二元分類的問題。

上圖中左圖是使用CART+random combination C A R T + r a n d o m   c o m b i n a t i o n 的結果；中圖是使用bootstrap b o o t s t r a p 機制選擇了N′(=N/2) N ′ ( = N / 2 ) 個樣本訓練的Decision Tree D e c i s i o n   T r e e 決策樹，使用的方法是CART+random combination C A R T + r a n d o m   c o m b i n a t i o n ，因為只是使用了原始數據的一半，所有存在一些劃分錯誤的點；右圖是使用一棵決策樹組成的random forest r a n d o m   f o r e s t ，所以和中圖得到的結果是一樣的。
接下來我們想要觀察的是，當樹的個數增多的時候，random forest r a n d o m   f o r e s t 的表現，也就是右圖的表現。

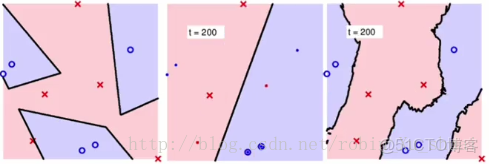
中圖是使用bootstrap b o o t s t r a p 機制選擇了N′(=N/2) N ′ ( = N / 2 ) 個樣本訓練的Decision Tree D e c i s i o n   T r e e 決策樹（第200棵）。右圖表現的是綜合200棵樹的表現。

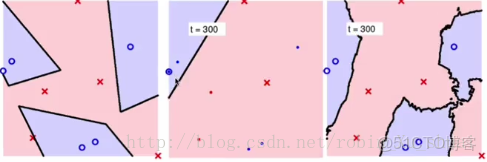
中圖是使用bootstrap b o o t s t r a p 機制選擇了N′(=N/2) N ′ ( = N / 2 ) 個樣本訓練的Decision Tree D e c i s i o n   T r e e 決策樹（第300棵）。右圖表現的是綜合300棵樹的表現。

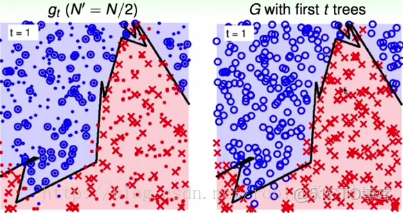
中圖是使用bootstrap b o o t s t r a p 機制選擇了N′(=N/2) N ′ ( = N / 2 ) 個樣本訓練的Decision Tree D e c i s i o n   T r e e 決策樹（第800棵）。右圖表現的是綜合800棵樹的表現。

這時我們觀察到由CART+random combination C A R T + r a n d o m   c o m b i n a t i o n 算法在bagging b a g g i n g 中的bootstrap b o o t s t r a p 機制得到的不同的訓練樣本上得到的800 800 棵Decision Tree D e c i s i o n   T r e e 組成的random forest r a n d o m   f o r e s t 算法得到的邊界（右圖）大概會通過◯ ◯ 和× × 的中間， 而只有一棵樹的時候，通常是不會有這樣的效果的（左圖） 。通過◯ ◯ 和× × 的中間正是我們在SVM S V M 中講過的large margin l a r g e   m a r g i n 。 另外使用random forest r a n d o m   f o r e s t 得到的邊界要比單一的一棵樹CART C A R T 得到的邊界要平滑的多。 所以random forest r a n d o m   f o r e s t 這樣利用了很多棵樹之後做出了平滑並且具有large margin l a r g e   m a r g i n 性質的邊界。

4.2 - 資料2

稍微複雜一點的資料。

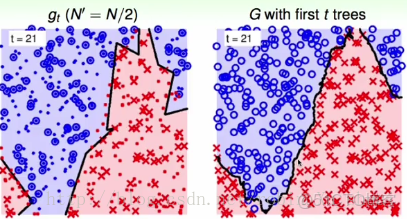
左圖是使用bootstrapping N′(=N/2) b o o t s t r a p p i n g   N ′ ( = N / 2 ) 得到的邊界；右圖是使用這一棵樹得到的random forest r a n d o m   f o r e s t 。

左圖是使用bootstrapping(N′=N/2) b o o t s t r a p p i n g ( N ′ = N / 2 ) 得到的邊界（在第21輪中）；右圖是使用這21棵樹得到的random forest r a n d o m   f o r e s t 的結果。這樣的非線性邊界比起左圖中的邊界要魯棒很多，具有比較平滑比較穩定的特性。

4.3 - 資料3

資料2+10%噪聲

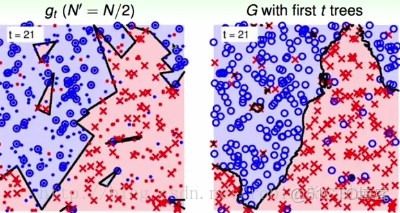
左圖是使用bootstrapping N′(=N/2) b o o t s t r a p p i n g   N ′ ( = N / 2 ) 得到的邊界；右圖是使用這一棵樹得到的random forest r a n d o m   f o r e s t 。可以看到在圖中決策樹給出的邊界中有一部分在努力的去過擬合那些噪聲。

左圖還是一棵決策樹的表現，右圖是使用21棵樹構成的random forest r a n d o m   f o r e s t ，可以看出邊界已經很平滑，雖然還有少數的邊界在擬合噪聲。但是通過randomforest r a n d o m f o r e s t 這種投票的機制，已經可以避免很多由噪聲產生的影響。(noise corrected by voting) ( n o i s e   c o r r e c t e d   b y   v o t i n g )

因為random forest r a n d o m   f o r e s t 的理論假設是當使用無限多棵樹的時候，會得到比較好的結果，所以一般來説我們會使用盡量多的樹。

小測試

下面的哪一個不是random forest r a n d o m   f o r e s t 的正確用法

1. 使用bootstrapped 的表現
2. 使用
3. 固定樹的數量

顯然答案應該是4，樹的數量要視具體的問題來決定。

5 - 總結

這篇介紹了Random Forest R a n d o m   F o r e s t 算法。這個算法的本質是將bagging b a g g i n g 算法中的base algorithm b a s e   a l g o r i t h m 使用decision tree d e c i s i o n   t r e e 。通常我們會把decision tree d e c i s i o n   t r e e 的過程利用randomly projected r a n d o m l y   p r o j e c t e d 添加一點隨機性，也就是用通過隨機結合的各式各樣的feature f e a t u r e 來做切分的決策。同時在這個算法中由於使用了bootstrap b o o t s t r a p 的機制，所以我們可以得到一些OOB O O B 的數據來驗證算法表現的好壞，而不必使用使用validation data v a l i d a t i o n   d a t a 來做validation v a l i d a t i o n 。也就是這個算法可以self validation s e l f   v a l i d a t i o n 。 另外這個自我驗證的方式可以配合permutation test p e r m u t a t i o n   t e s t 可以來做feature selection f e a t u r e   s e l e c t i o n 。最後我們説到當樹的數量夠多的時候，我們可以得到相對平滑的邊界。
Random forest R a n d o m   f o r e s t 是bagging b a g g i n g 和decision tree d e c i s i o n   t r e e 的結合。下一篇我們介紹的boosted decision tree b o o s t e d   d e c i s i o n   t r e e 是AdaBoost A d a B o o s t 和decision tree d e c i s i o n   t r e e 的結合。