文章目錄

  • 邏輯迴歸（分類）
  • 1、基本原理
  • 4、梯度下降法
  • 4、sklearn實現邏輯迴歸
  • 5、多分類問題
  • 5.1多分類原理
  • 5.2sklearn實現多分類

邏輯迴歸（分類）

1、基本原理

邏輯迴歸用於分類，是對樣本屬於某一類的概率進行預測，對數機率函數：
sklearnLogisticRegression多分類_機器學習

給定數據集sklearnLogisticRegression多分類_機器學習_02,其中sklearnLogisticRegression多分類_取值_03表示第sklearnLogisticRegression多分類_機器學習_04個樣本點sklearnLogisticRegression多分類_取值_05(表示有n個屬性值)。
考慮到sklearnLogisticRegression多分類_取值_06取值是連續的，因此它不能擬合離散變量。可以考慮用它來擬合條件概率 ，因為概率的取值也是連續的。但是其取值為 R ，不符合概率取值為 0 到 1，因此考慮採用廣義線性模型。
對於一個簡單的二分類問題，我們用logistics函數來代替理想的階躍函數來作為連接函數：
sklearnLogisticRegression多分類_多分類_07
令sklearnLogisticRegression多分類_機器學習_08

於是有：
sklearnLogisticRegression多分類_取值_09
事件發生與不發生的概率比值稱為機率（odds）,sklearnLogisticRegression多分類_多分類_10表示發生的概率，即：
sklearnLogisticRegression多分類_取值_11
綜合兩式可得：
sklearnLogisticRegression多分類_多分類_12
因此邏輯迴歸的思路是，先擬合決策邊界(不侷限於線性，還可以是多項式，這個過程可以理解為感知機)，再建立這個邊界與分類的概率聯繫（通過對數機率函數），從而得到了二分類情況下的概率。

關於對數似然估計的概念我這裏就不作過多介紹了，可參考浙江大學的《概率論與數理統計》，我們由“最大似然估計法”去得出代價函數，我們要求每個樣本屬於其真實標記的概率越大越好，所以：
sklearnLogisticRegression多分類_機器學習_13
取“對數似然”得：
sklearnLogisticRegression多分類_多分類_14
由上，我們將代價函數定為：
sklearnLogisticRegression多分類_取值_15
一次性計算出所有樣本的預測值（是個概率值）:
sklearnLogisticRegression多分類_多分類_16
其中，sklearnLogisticRegression多分類_機器學習_17表示訓練集，sklearnLogisticRegression多分類_取值_18
將代價函數寫成矩陣形式：
sklearnLogisticRegression多分類_多分類_19
其中，sklearnLogisticRegression多分類_取值_20表示由所有訓練樣本輸出構成的向量，sklearnLogisticRegression多分類_取值_21表示計算得出所有樣本的預測值（是個概率值）

4、梯度下降法

梯度下降公式：
sklearnLogisticRegression多分類_機器學習_22
【logistics迴歸梯度下降公式的簡單推導】
sklearnLogisticRegression多分類_多分類_23

4、sklearn實現邏輯迴歸

# -*- coding: utf-8 -*-
"""
Created on Tue Nov 12 19:28:12 2019

@author: 1
"""

from sklearn.model_selection import train_test_split
#導入logistics迴歸模型
from sklearn.linear_model import LogisticRegression
import numpy as np
import pandas as pd


df=pd.read_csv('D:\\workspace\\python\machine learning\\data\\breast_cancer.csv',sep=',',header=None,skiprows=1)
X = df.iloc[:,0:29]
y = df.iloc[:,30]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
model = LogisticRegression(solver='liblinear')
model.fit(X_train, y_train)
train_score = model.score(X_train, y_train)#R2值越接近1越好
cv_score = model.score(X_test, y_test)
print('train_score:{0:.6f}, cv_score:{1:.6f}'.format(train_score, cv_score))

y_pre = model.predict(X_test)
y_pre_proba = model.predict_proba(X_test)#輸出概率

print('matchs:{0}/{1}'.format(np.equal(y_pre, y_test).shape[0], y_test.shape[0]))#shape[0]列，shape[1]行
#print('y_pre:{}, \ny_pre_proba:{}'.format(y_pre, y_pre_proba))#輸出概率預測值

5、多分類問題

5.1多分類原理

為了實現多分類，我們將多個類(D)中的一個類標記為正向類(y=1），然後將其他所有類都標記為負向類，這個模型記作sklearnLogisticRegression多分類_多分類_24 。接着，類似地第我們選擇另一個類標記為正向類(y=2)，再將其它類都標記為負向類，將這個模型記作 sklearnLogisticRegression多分類_取值_25 依此類推。最後我們得到一系列的模型簡記為：
sklearnLogisticRegression多分類_取值_26其中sklearnLogisticRegression多分類_多分類_27
最後，在做預測時，對每一個輸入的測試變量，我們將所有的分類機都運行一遍，選擇可能性最高的分類機的輸出結果作為分類結果：
sklearnLogisticRegression多分類_取值_28

5.2sklearn實現多分類

# -*- coding: utf-8 -*-
"""
Created on Tue Nov 12 22:07:34 2019

@author: 1
"""

from sklearn.model_selection import train_test_split
#導入logistics迴歸模型
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score#預測準確率
import pandas as pd
import matplotlib.pyplot as plt


df=pd.read_csv('D:\\workspace\\python\machine learning\\data\\iris.csv',sep=',')
X = df.iloc[:,0:1]
y = df.iloc[:,4]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
model = LogisticRegression(solver='liblinear')
model.fit(X_train, y_train)
y_pre=model.predict(X_test)
print('accuracy_score：{}'.format(accuracy_score(y_test,y_pre)))#預測準確率
y_pre_proba = model.predict_proba(X_test)
print('y_pre:{}, \ny_pre_proba:{}'.format(y_pre, y_pre_proba))#輸出概率預測值

#畫原始數據圖
colors = ['blue', 'red','green']
plt.figure(1)
for i in range(3):
    plt.scatter(df.loc[df['virginica']==i].iloc[:,0],df.loc[df['virginica']==i].iloc[:,1],c=colors[i])
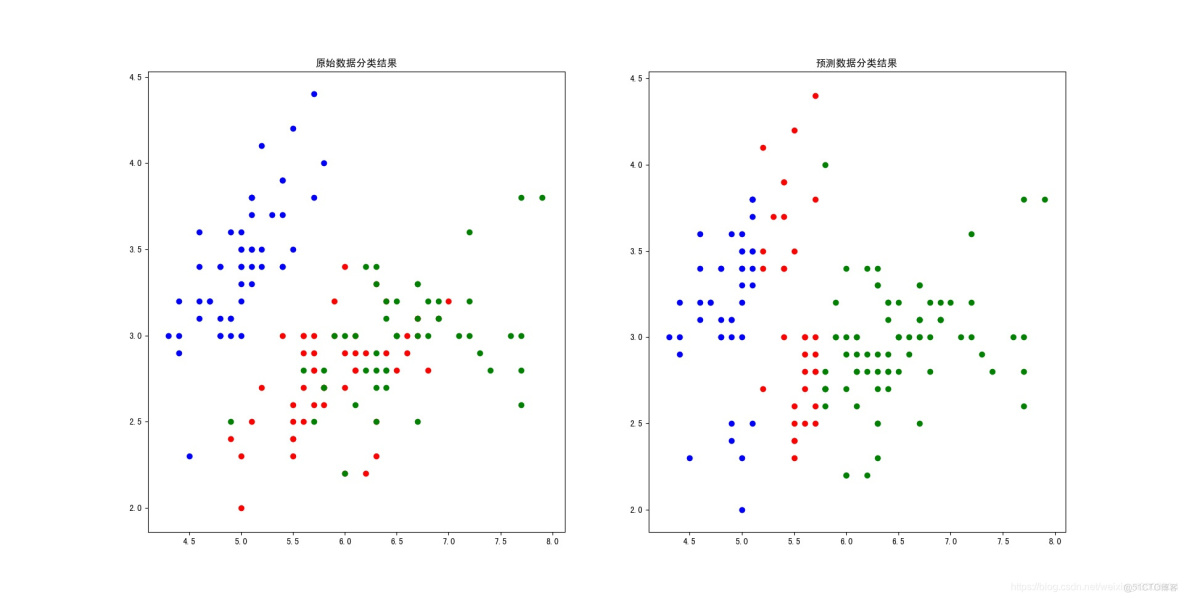
plt.title('原始數據分類結果')

#畫分類結果圖
colors = ['blue', 'red','green']
plt.figure(2)
df['virginica_pre']=model.predict(X)
for i in range(3):
    plt.scatter(df.loc[df['virginica_pre']==i].iloc[:,0],df.loc[df['virginica_pre']==i].iloc[:,1],c=colors[i])
plt.title('預測數據分類結果')

結果可視化：


sklearnLogisticRegression多分類_取值_29