在 STL 的 map、set 等關聯容器底層,平衡二叉搜索樹是保證高效增刪查改的關鍵數據結構。而 AVL 樹作為最早的平衡二叉搜索樹之一,其核心思想是通過維持樹的高度平衡,避免普通二叉搜索樹在極端情況下退化為鏈表,從而將時間複雜度穩定在 O (log n) 級別。本文將結合理論原理與代碼實現,帶大家走進 AVL 樹的世界(旋轉操作將在下一篇詳細拆解,敬請期待)。
目錄
一、AVL 樹的核心定義與性質
1. 基本性質要求
2. 平衡因子(Balance Factor)
二、AVL 樹的性能優勢
三、AVL 樹的節點與結構設計
1. 節點結構(Node)
2. AVL 樹類結構
四、AVL 樹插入操作:三步核心流程
第一步:按 BST 規則插入節點
第二步:向上回溯更新平衡因子
核心更新規則
更新終止條件
第三步:處理不平衡(旋轉調整預告)
五、總結與下一篇預告
一、AVL 樹的核心定義與性質
AVL 樹的名字源於其發明者 Adelson-Velsky 和 Landis,它本質上是一棵 "滿足平衡條件的二叉搜索樹",兼具二叉搜索樹的有序性和自身的平衡性。
1. 基本性質要求
- 基礎前提:必須是一棵二叉搜索樹(BST),即左子樹所有節點值 <根節點值,右子樹所有節點值> 根節點值(保證有序性,支持二分查找);
- 平衡核心:任意節點的左右子樹高度差(平衡因子)的絕對值 ≤ 1;
- 遞歸特性:平衡要求不僅適用於根節點,所有子樹都需遞歸滿足;
- 平衡限制原因:並非追求左右子樹高度完全相等(如 2 個、4 個節點時無法實現),而是允許最大 1 的高度差,兼顧實用性與平衡性。
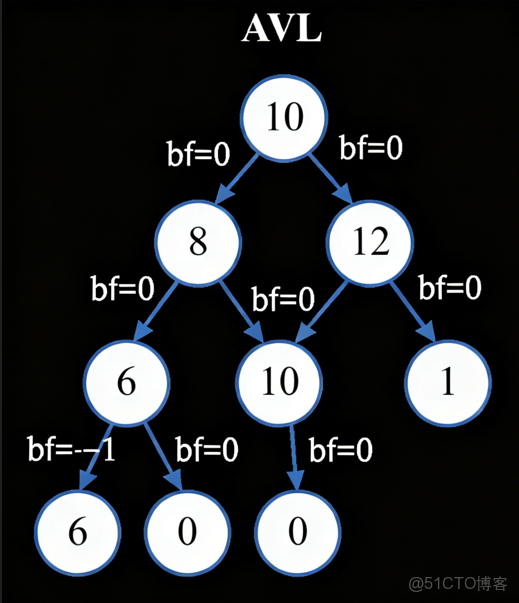
2. 平衡因子(Balance Factor)
平衡因子是 AVL 樹判斷平衡狀態的核心指標:
- 定義:平衡因子(bf)= 右子樹高度 - 左子樹高度;
- 合法取值:-1(左子樹比右子樹高 1)、0(左右子樹等高)、1(右子樹比左子樹高 1);
- 實現細節:每個節點需存儲平衡因子,且建議使用三叉鏈(left/right/parent 指針),方便回溯更新平衡因子。
二、AVL 樹的性能優勢
AVL 樹通過嚴格的平衡條件,保證了增刪查改的時間複雜度均為 O (log n),這一效率優勢在大數據量下尤為明顯:
- 10 億條數據:最多隻需 30 次比較(2³⁰≈10⁹);
- 1 萬億條數據:最多隻需 40 次比較(2⁴⁰≈10¹²);
- 對比普通 BST:普通 BST 在最壞情況下(如有序插入)會退化為鏈表,時間複雜度變為 O (n),而 AVL 樹通過平衡調整避免了這一問題。
三、AVL 樹的節點與結構設計
1. 節點結構(Node)
AVL 樹的節點需要存儲鍵值對、指針信息和平衡因子,採用模板類實現以支持泛型:
template<class K, class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left; // 左孩子指針
AVLTreeNode<K, V>* _right; // 右孩子指針
AVLTreeNode<K, V>* _parent; // 父節點指針(三叉鏈)
int _bf; // 平衡因子
pair<K, V> _kv; // 鍵值對存儲
// 構造函數
AVLTreeNode(const pair<K, V>& kv)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _bf(0) // 新節點初始平衡因子為0(左右子樹均為空)
, _kv(kv)
{}
};2. AVL 樹類結構
AVL 樹類需包含根節點指針,並提供核心操作接口(本文重點講解插入):
template<class K, class V>
class AVLTree
{
typedef AVLTreeNode<K, V> Node; // 節點類型別名,簡化代碼
public:
bool Insert(const pair<K, V>& kv); // 插入接口(核心)
private:
Node* _root = nullptr; // 根節點初始化為空
};四、AVL 樹插入操作:三步核心流程
AVL 樹的插入操作是平衡維護的關鍵,需遵循 "先按 BST 規則插入,再更新平衡因子,最後處理不平衡" 的三步流程。
第一步:按 BST 規則插入節點
插入邏輯與普通二叉搜索樹一致,核心是找到合適的插入位置,並通過三叉鏈建立節點間的關聯:
- 若樹為空,直接創建根節點;
- 否則從根節點出發,根據鍵值大小遍歷(比當前節點小則走左子樹,大則走右子樹),找到插入位置(cur 為空時);
- 創建新節點,通過父節點指針(parent)建立雙向關聯(新節點的 parent 指向父節點,父節點的 left/right 指向新節點);
- 若插入鍵值已存在,返回 false(AVL 樹不允許重複鍵)。
代碼實現:
bool Insert(const pair<K, V>& kv)
{
// 情況1:樹為空,直接創建根節點
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
// 情況2:樹非空,查找插入位置
Node* parent = nullptr;
Node* cur = _root;
while (cur != nullptr)
{
if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
// 鍵值已存在,插入失敗
return false;
}
}
// 情況3:創建新節點並鏈接到父節點
cur = new Node(kv);
if (parent->_kv.first > kv.first)
{
parent->_left = cur; // 新節點是父節點的左孩子
}
else
{
parent->_right = cur; // 新節點是父節點的右孩子
}
cur->_parent = parent; // 雙向關聯父節點
// 後續:更新平衡因子 + 處理不平衡(見下文)
// ...
}第二步:向上回溯更新平衡因子
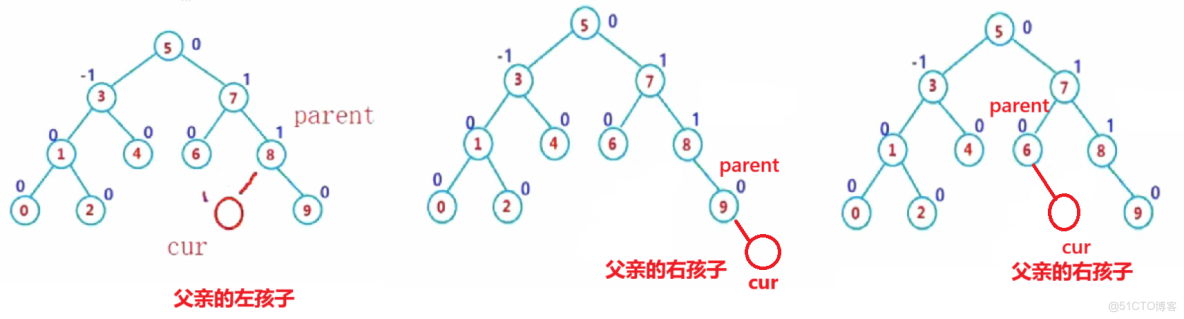
新節點插入後,會導致其所有祖先節點的子樹高度可能發生變化,因此需要從插入節點的父節點開始,向上回溯更新平衡因子:
核心更新規則
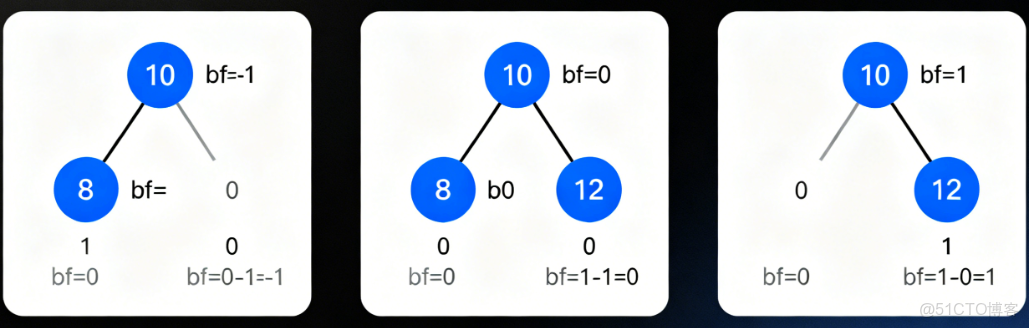
- 若新節點是父節點的左孩子:父節點的平衡因子 -= 1(左子樹高度增加,平衡因子減小);
- 若新節點是父節點的右孩子:父節點的平衡因子 += 1(右子樹高度增加,平衡因子增大)。
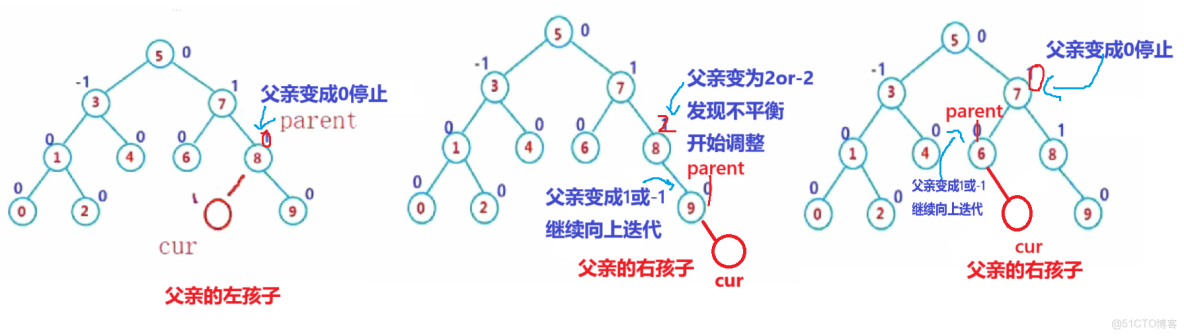
更新終止條件
- 當某祖先節點的平衡因子變為0:説明該節點的左右子樹高度恢復平衡,子樹總高度未變化,無需繼續向上更新(類比 "填平了較矮的子樹");
- 當某祖先節點的平衡因子變為 **±1**:説明該節點的子樹高度增加了 1,需要繼續向上更新(高度變化會傳導給更上層的祖先);
- 當某祖先節點的平衡因子變為 **±2**:説明該子樹出現不平衡,需要立即停止更新,進入旋轉調整階段。
代碼實現(接插入邏輯後):
// 插入後開始更新平衡因子
while (parent != nullptr)
{
// 1. 根據新節點是左/右孩子,更新父節點平衡因子
if (cur == parent->_left)
{
parent->_bf--; // 左孩子插入,bf-1
}
else // cur == parent->_right
{
parent->_bf++; // 右孩子插入,bf+1
}
// 2. 判斷是否需要繼續更新或處理不平衡
if (parent->_bf == 0)
{
// 子樹高度未變化,終止更新
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
// 子樹高度變化,繼續向上更新
cur = parent;
parent = cur->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
// 子樹出現不平衡,需要旋轉調整
// 旋轉邏輯(下一篇詳細講解)
// ...
// 旋轉後子樹高度恢復,終止更新
break;
}
}
return true;第三步:處理不平衡(旋轉調整預告)
當某祖先節點的平衡因子變為 ±2 時,説明該子樹已經失衡,此時必須通過旋轉操作來恢復平衡。AVL 樹的不平衡場景分為四種:
- 左左型(LL):失衡節點的平衡因子為 - 2,且其左孩子的平衡因子為 - 1;
- 左右型(LR):失衡節點的平衡因子為 - 2,且其左孩子的平衡因子為 1;
- 右右型(RR):失衡節點的平衡因子為 2,且其右孩子的平衡因子為 1;
- 右左型(RL):失衡節點的平衡因子為 2,且其右孩子的平衡因子為 - 1。
對應的解決方案是單旋(LL/RR 場景)或雙旋(LR/RL 場景),旋轉的核心思想是通過局部子樹重組,降低子樹高度差,恢復平衡因子的合法範圍。