一、基於度量的程序結構分析

0. 面向對象的度量指標

主要度量指標分為基本複雜度、模塊設計複雜度和圈複雜度。以下進行詳細解釋：

• 基本複雜度 ev(G)：描述程序非結構化程度。ev(G)高的程序難以模塊化和維護。

非結構化：難以結構化的部分。此部分中，程序的質量較低，代碼維護難度較大。

• 模塊設計複雜度 iv(G)：描述模塊判定結構，即調用關係，體現為耦合度。iv(G)高的程序難以維護與複用。
• 圈複雜度 v(G)：描述模塊判定結構的複雜程度，體現為獨立路徑的條數。v(G)高的程序同樣難於測試和維護，代碼質量低。

三種度量指標中，模塊設計複雜度iv(G)往往遠小於圈複雜度。其中，高的圈複雜度與程序存在錯誤具有很大關係。

此外，度量指標還包含以下三種複雜度。

• OCavg：平均操作複雜度；
• OCmax：最大操作複雜度；
• WMC： 加權方法複雜度。

1. 第一次作業

作業思路

• 由於不要求格式判斷，在正式解析之前，對輸入進行預處理：

• 替換空格
• 合併符號

• 正式處理部分：

• 採用正則表達式進行判斷，使用ArrayList鏈表存放因子；
• 在多項式類中設計求導方法，對ArrayList中的元素進行求導；
• 合併同類項，進行輸出。

重要類/接口分析

• Main類：

• 處理輸入；
• 解析項加入鏈表；
• 合併輸出。

• Poly類：

• 解析項的輸出方式；
• 實現求導功能。

代碼可視化與數據統計的程序度量

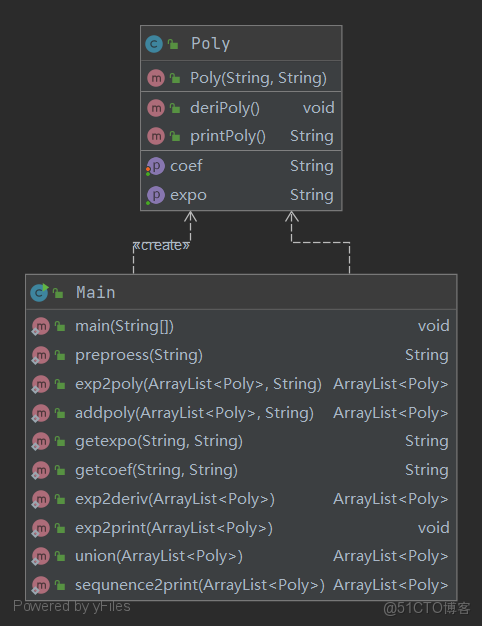
程序UML類圖

第一次作業中，我一共創建了2個類。通過類圖可以發現，本次作業未引入工廠模式，導致大量方法堆疊在Main函數中，無法擁有一個可擴展的層次結構。嘗試從面相過程的編程思想轉變為面相對象的編程思想，但實現起來並未完全面相對象，這也是第一次作業的不足之處，以及與以往編程方式不同的提升之處。

• 代碼規模分析

分析來看，主函數中容納了大部分代碼量，這種情況由於未使用工廠模式導致，並不是一個良好的解決方式，但這在後續作業中得以解決。

• 類複雜度分析

分析來看，大多數操作被集中於Poly類中，而基於面向對象的編程的合理方式是使用工廠模式，將處理方法置於工廠類當中，對象類中進行處理的高操作複雜度不是良好的程序結構，也正體現了這種模式的不足之處以及可待改進之處。

方法複雜度分析

分析來看，整體的複雜程度和耦合程度較低，但例如Poly.printPoly()方法由於處理不當導致ev(G)等超標。經分析， 原因是在項的輸出中需要考慮大量指數為1與係數為1等的省略情況，含有較多的 if-else 分支，這也正是這類問題的共性所在。由於第一次作業將這些因子放在同一類處理，也是使這種情況被放大的原因。

優缺點分析

• 優點分析

• 採用容器存儲，處理層次化
• 化簡功能較為完善

• 缺點分析

• 未使用工廠模式，項目結構失衡
• 面向對象的思維方式、程序的可擴展性有待提升

評測結果

第一次作業在強測與互測階段沒有被找出bug，找出了同房間內的一個bug，將會在bug分析中詳述。

2. 第二次作業

作業思路

本次作業有兩種主要思路：

• 基於容器建立項類，在項中添加多個容器屬性。

• 優缺點分析

• 優點：符合計算依從思想，實現對錶達式進行化簡（合併同類項）更加容易。
• 缺點：求導複雜。

• 基於數據結構建立表達式樹，將各類因子繼承於父類Factor，並將父類引用作為樹結點，進行鏈式求導（對樹進行遍歷）。

• 優缺點分析

• 優點：符合數據依從思想，實現因子管理更加容易。
• 缺點：化簡複雜。

正如教程所言，面對優化應優先考慮正確性，因此，我採用更加保證求導正確性的表達式樹方法進行處理，將項與因子分別建立類，使用二叉樹進行結構構造。處理思路如下：

• 基於表達式的加減符號，提取出各個項。

• 基於項中因子的結構，例如a*x**b，實現從項到Factor的拆分。
• 在拆分過程中，對各Factor進行分類，在該父類下納入如三角函數因子等多個子類。
• 在子類中進行因子求導。
• 對樹進行遍歷，將求導結果進行最終輸出。

• 具體地，構建表達式樹採用向上的方式，即匯聚本深度下的子樹，形成自身的新樹，對上一深度依次進行處理：

• 對於表達式，首先讀入表達式，將每一項在工廠中拆分表達式返回的樹根節點使用運算符+連接，形成一個新的表達式樹。
• 對於項，根據表達式形成的項，將每一項在工廠中拆分項返回的樹根節點使用運算符*連接，形成一個新的表達式樹。
• 對於因子，根據項形成的因子，將每一項在工廠中使正則表達式匹配因子類型，形成Factor樹。

• 將本次使用的表達式樹方法繼續深入來看，對於每一個類，即抽象為樹節點，內部主要涵蓋求導與輸出兩種主要方法：

• 求導：對以本結點作為根的子樹求導，返回的一個求導後的根節點。
• 輸出：對以本結點作為根的子樹輸出，返回的一個字符串。

重要類/接口分析

• 輸入處理：Factory, Main

• Factory類：工廠類，完成輸入處理，包括表達式的拆分與項的拆分
• Main類：主函數，完成輸入預處理，如符號替換

• 表達式樹：Derivebrackets, Parameter, Power, Term, Trigle

• Derivebrackets類：存放嵌套類，包括求導、輸出功能
• Parameter類：存放常數類，包括求導、輸出功能
• Power類：存放冪函數類，包括求導、輸出功能
• Trigle類：存放三角函數類，包括求導、輸出功能

• 求導化簡：Derivemult, Derivemult1, Derivemult2, Deriveplus, Superior

• Derivemult類：實現乘法求導
• Deriveplus類：實現加法求導
• Superior類：化簡表達式

代碼可視化與數據統計的程序度量

程序UML類圖

在第二次作業在我一共創建了12個類，這主要被劃分為3個部分。

代碼規模分析

分析來看，由於採用了工廠模式，主函數內代碼規模得以改善，然而，由於大量的if-else操作，導致求導部分代碼規模量巨大，實際上，這是不好的設計架構與未完善的面向對象方式所造成，我在第三次作業中改善了這一點。

類的複雜度分析

分析來看，設計到求導的Derivemult類中存在很大複雜度，這是由於未將求導設計為接口，導致結構化不強。同時內部使用了大量的if-else語句，造成了很大的複雜度，但本次引入了工廠模式，對於簡化操作與可擴展性有所幫助。

方法的複雜度分析

由於方法數目較多，Method Metrics 生成表格過長，故只展示總體情況與出現紅色的條目。

分析來看，整體的複雜程度和耦合程度集中於程序的化簡部分，這造成了一定的資源浪費。而複雜的化簡流程也造成了一定錯誤的產生，損失了面向對象過程的帶來的優越性，但可擴展性較第一次作業得以增強。出於第二次作業的複雜，我在第三次作業進行了簡化。

優缺點分析

• 優點分析

• 採用工廠模式，結構較為清晰
• 可擴展性得以提升

• 缺點分析

• 存儲操作未處理好
• 部分嵌套處理混亂

評測結果

第二次作業由於優化過度造成了強測中的2個bug，互測階段也被找出了4個bug，找出了同房間內存在的7個bug。

3. 第三次作業

作業思路

本次作業基於第二次作業進行迭代改進，優化工廠模式，進行增量開發。主要修改了以下內容：

• 求導方式；
• 化簡方式；
• 增加了格式檢查；
• 三角函數sin和cos的屬性與解析方式；
• 實現了三角函數的嵌套求導。

對於格式判斷，使用大正則表達式會導致爆棧出錯，是不可取的操作。

因此，我採用了遞歸的方式，通過利用#替代嵌套，將#納入符合的格式要求，實現格式檢查。

比如(3*x+2)*cos(x)：

在我使用的方法中，即可將它轉換為#*cos(x)，對其進行項的格式檢查即可，深層嵌套通過遞歸以此類推。其他具體思路與第二次作業大體相同。

重要類/接口分析

• 格式判斷和輸入處理：Factory, Main

• Factory類：工廠類，完成輸入處理，包括表達式的拆分與項的拆分，實現格式判斷
• Main類：主函數，完成輸入預處理，如符號替換

• 表達式樹：Expression, poly, Factor, Constant, Power, Tricos, Trisin, Brackets

• Expression類：存放表達式，形成表達式樹，包括求導、輸出功能
• poly類：存放項類，構成項結點，包括求導、輸出功能
• Factor類：存放因子類，構成因子結點，包括求導、輸出功能
• Constant類：存放常數類，構成常數結點，包括求導、輸出功能
• Power類：存放冪函數類，構成冪函數結點，包括求導、輸出功能
• Tricos類：存放三角函數類，構成三角函數結點，包括求導、輸出功能
• Trisin類：存放三角函數類，構成三角函數結點，包括求導、輸出功能
• Brackets類：存放嵌套類，構成嵌套結點，包括求導、輸出功能

• 求導化簡：Factory

• Factory類：處理工廠，包括解析表達式，以及化簡功能

代碼可視化與數據統計的程序度量

程序UML類圖

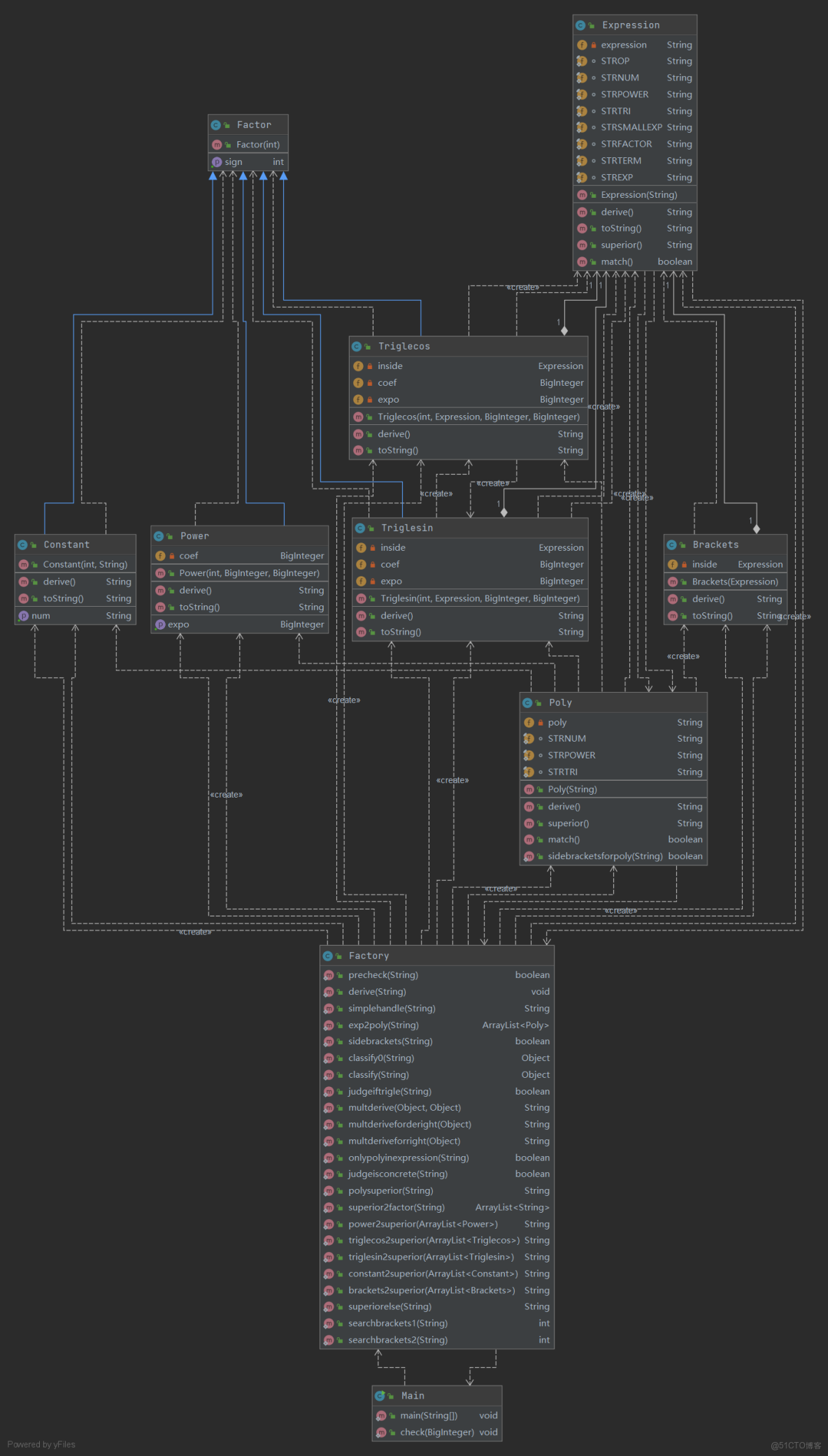
在第二次作業中我一共創建了共包含10個類，這主要被劃分為3個部分。

代碼規模分析

分析來看，由於以面向對象的方法作為指導，進行了良好架構的設計與優化，本次作業代碼規模比上次大大減少，同時除了工廠需要進行大量處理操作之外，其他類的規模合理，沒有臃腫龐大的類。

類的複雜度分析

分析來看，在本次作業架構的設計上，我使用了很好的面向對象的處理方式，將主要對象分為Expression, Poly, Factor類，其下包含了如下的繼承類，即Constant, Brackets, Triglecos, Tirglesin, Power。課程教授的內容也使我能夠很好地接受高內聚低耦合帶來的便利。

方法的複雜度分析

分析來看，主要的複雜度出現在對於格式檢查的處理上，由於我將格式檢查和多項式求導分成了不相關的兩個模塊，造成了部分的重複，使得格式檢查中複雜度增大。而對於多項式的計算部分，我使用了面向對象的方式進行處理與分析，複雜度相比第二次作業改進許多，這是我認為我做的比較好的地方。

優缺點分析

• 優點分析

• 採用工廠模式，結構清晰
• 可擴展性良好
• 面向對象思維方式，可靠性改善

• 缺點分析

• 化簡操作有待提升

評測結果

第三次作業中由於對面向對象思想的良好吸收與運用，在強測中沒有出現bug，由於在格式檢查中的一個小筆誤，造成了互測中被測出了1次bug。同房間內實現較好，沒有測出他人的bug。

二、程序的bug分析

自身程序bug

1. 第一次作業

強測與互測均沒有出現bug。

2. 第二次作業

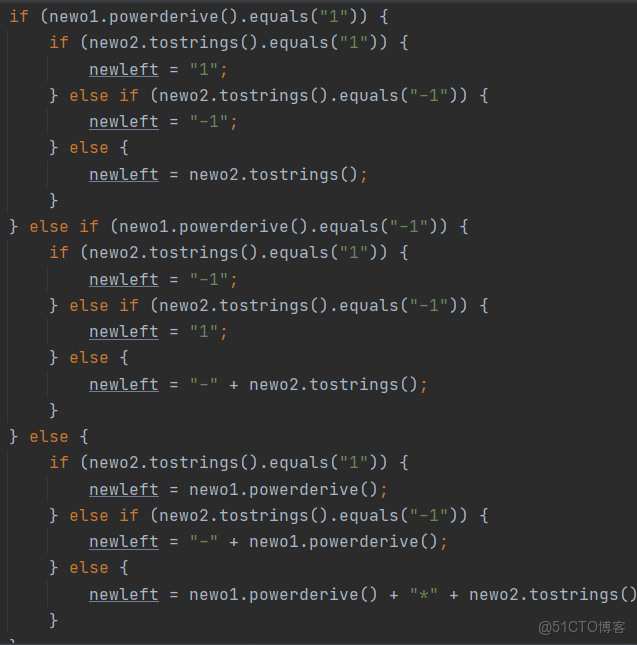
強測出現了兩個bug，其一是由於內部處理不好的遞歸調用，位於求導類，造成了程序超時，分析後發現，內部過多的tostring()語句是造成它的主要原因。具體改進是，應該將其首先存入一個變量之中，而後調用變量即可，因為多次調用tostring()語句實際上是在調用類中的某個函數，將函數重新運行一遍，而變量即可解決這一問題。

對於另一個的bug，是由於化簡造成，位於工廠類的化簡方法中。我誤將項中因子的化簡合併的*號當做+號，將第一次作業中合併同類項的代碼直接複製使用，造成了這一錯誤的出現。

我對此的感想是，未來代碼的模塊即使與在之前的作業中實現過，也應該再次認真地敲一遍，而不是直接複製粘貼。

互測中被hack的bug也是同樣造成的，修復了以上2個bug的主要問題後，強測、互測均通過。

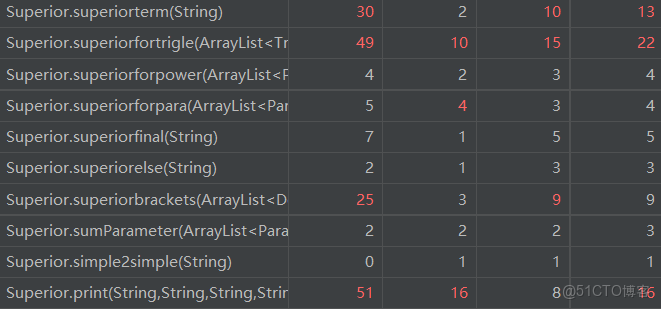
代碼行和圈複雜度的差異

出現bug方法的代碼如下：

如上所述，大量使用toString()導致了錯誤，這也導致如上所示的代碼行大大增多（由前文代碼規模也可見）。同時，根據前文圈複雜度的列舉，可以發現該模塊（求導模塊）的圈複雜度也相比其他未出現bug的方法模塊要高許多。

3. 第三次作業

強測中沒有出現bug。在互測中bug存在於如下的筆誤之中：

for(i=str.length-1; i>=0; i++) {
    ...
}

由於慣性思維，錯把i--寫成i++，導致了程序出現了bug。

代碼行和圈複雜度的差異

由於該bug的特殊性，沒有對代碼行與圈複雜度造成影響。

綜上所述，也説明了無論對於多麼好的設計，如果實現的細節沒有到位，那麼仍會導致同樣的結果。因此，我對此的感想是以後應該更加細緻，注意程序的細節之處。

他人程序bug

1. 第一次作業

互測中我測出了他人一個bug。原因是其未對計算結果為0的情況進行考慮。

例如輸入：

x-x

其沒有任何輸出，正確的處理方式是對於結果為0時，即容器中不存在內容，應該輸出0。

2. 第二次作業

在第二次作業中，我利用評測機與手動構建邊緣樣例，測試出了他人8個bug。

這些bug主要是由於內部嵌套的處理不足，而導致超時造成。可能出現錯誤的方式也與我相同，即多次調用了同一個toString()。這導致如下面對如下的測試用例，代碼無法運行完畢。

x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x*x

(((((((((((((((((x)))))))))))))))))

此外，對於0的處理也是很大的問題。

例如，應該在結果為：

(0)

的時候輸出(0)，但其錯誤地輸出了()，即缺少對於括號內元素的判斷，這也是應該注意的地方。

3. 第三次作業

本次作業互測中沒有發現bug。

發現bug的策略

本次我採取的測試策略：測評機黑箱測試 + 手動構建邊緣測試樣例。

測評機黑箱測試

實現自動測試的主要內容分為：

• 求導
• 化簡
• 比較

具體而言，首先對測試用例進行分類。例如常數、三角函數、嵌套類，再利用正則表達式生成字符串，進行針對性構造。由於數據長度的限制，生成數據時，應該生成長度直到小於等於50。此後，再利用python sympy庫中的diff等函數實現比較。

基於測評機的黑箱測試可以針對正確性進行測試。然而這難以覆蓋格式判斷以及超時造成的錯誤。因此，被需要引入手動構建的邊緣測試樣例。在實際操作中，也證明了此種方法在本次作業中尋找bug更加有效。

手動構建邊緣測試樣例

手動構建邊緣樣例的方式主要涵蓋以下三種：

• 極端數據
• 自己測試時出現的bug的數據
• 閲讀代碼尋找薄弱點

其具體説明如下：

1. 極端數據

手動構建用例更具有針對性，尤其是極端數據，它能夠覆蓋到邊緣的錯誤。

1. 自己測試時出現的bug的數據

由於許多bug在同學之間存在共性，所以對於使用自己測試時出現的bug的數據來測試別人，成功率相對而言比較高。

1. 閲讀代碼

閲讀代碼不但能找到他人代碼的薄弱之處，也能讓我們面向對象的良好設計代碼加以學習，進而改進自己的代碼。這部分正是結合被測程序的代碼設計結構。

但由於閲讀代碼比較耗時，我們應該有針對性地閲讀。例如重點閲讀面向過程的代碼，對於求導、化簡、遞歸、格式判斷是本次作業主要的出錯點。例如當對方代碼處理遞歸非常複雜時，可能出現超時現象，應構造相應的極端數據進行針對性hack，例如：

(((((((((((((((x)))))))))))))))

三、重構經歷總結

第三次作業重構

重構過程

本單元主要在第三次作業開發時重構瞭解析的遞歸調用方式和面向對象的類的存儲方式。

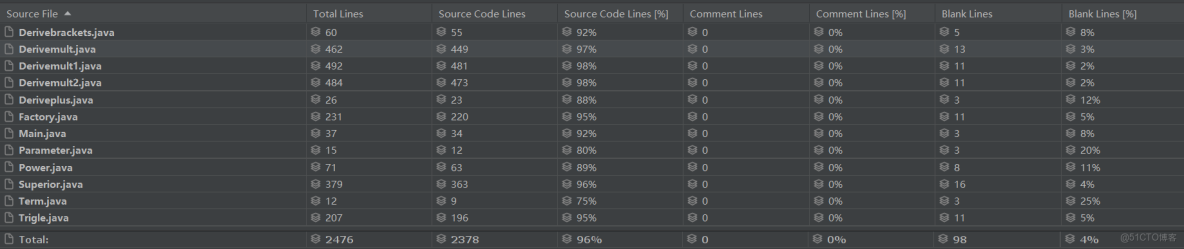
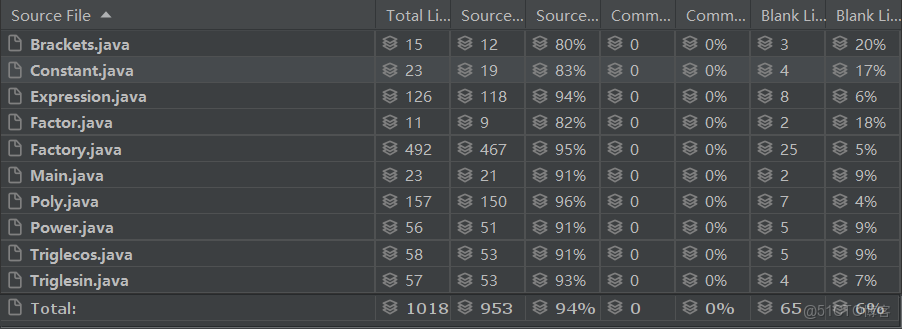
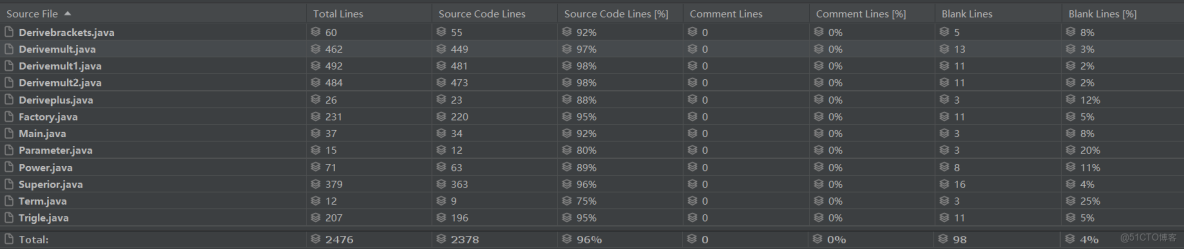
由於第一次作業較為簡單，未涉及需要進行遞歸的複雜表達式求導，或面向對象上許多類的存儲方式，因此不需要太多改動。第二次作業由於表達式嵌套的引入，以及三角函數的構成，在第一次簡單架構的基礎上進行一些刪改，即完成了第二次的構建，但正因如此，可擴展性無法保證，如下圖所示是重構前的度量數據：

在第三次作業的過程中，由於三角函數內也支持嵌套，因此便開展了重構過程。

在整個重構過程的開始，收到課程的啓發以及研討課的收穫，我先進行的是對對象的類的構建。以遞歸下降為指導，我定義了Expresssion, Poly和Factor三大類，作為表達式、項、因子這三種對象，基於此，我使用繼承的關係，在Factor的基礎上繼承了三角函數、常數、嵌套等子類。基於此，結合工廠模式，我開展了代碼的正式編寫。

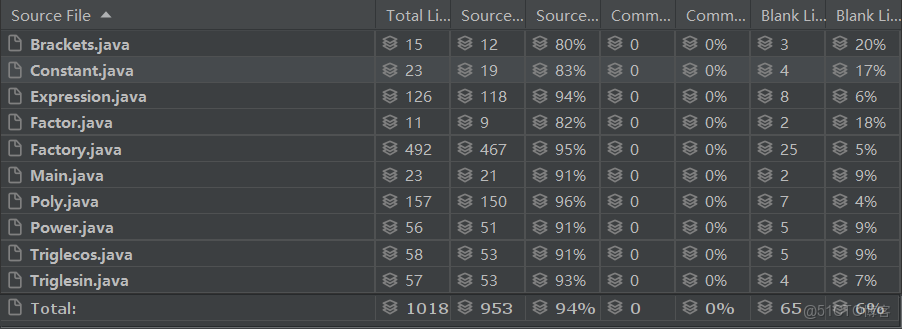
在編寫過程中，我以工廠模式作為指導，依託高內聚低耦合的思路對錶達式開展遞歸下降的解析，一些關於判斷或解析的主要函數我已經前兩次填寫完成，因此書寫代碼的時間並不長。最後實現的時候，整個代碼的性能、框架、複雜度、正確性都得到了極大的改善，以下是重構後的度量數據：

最後，在此基礎上我添加了格式判斷模塊，便完成了第三次作業的重構工作，由上述度量數據的對比可知，程序結構形成了較大改善，重構前代碼長度為2476，重構後代碼長度為1018，即僅用不到重構前不到一半的代碼長度便實現了可靠性更高的功能。

經驗總結

• 重構的過程中，我書寫代碼時的感受或心情與以往不同。這是因為經過重構後代碼非常具有結構化，思路非常清晰。因此，給我的感受是一定要先依託面向對象的思路來設計架構，而後進行代碼填寫。
• 完成代碼時，尤其是具有後續迭代的任務，應該考慮後續的工作，初期不要認為只滿足當下的要求即可，實際上去重構的時間會遠大於自己初期便設計好一個可擴展性的架構的時間。
• 針對本次重構，我對字符串的解析中遞歸下降法收穫頗豐，這可能有助於未來編譯原理的學習。因此，在未開始編寫代碼時，往往對於方法的思考或者查找，將大於自己隨心所欲的想法的效果，應該通過更多途徑去尋找任務良好的解決方案。