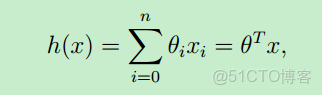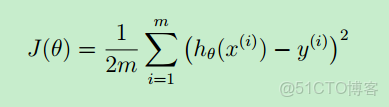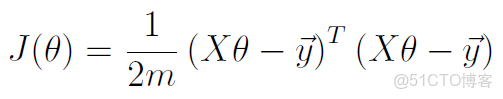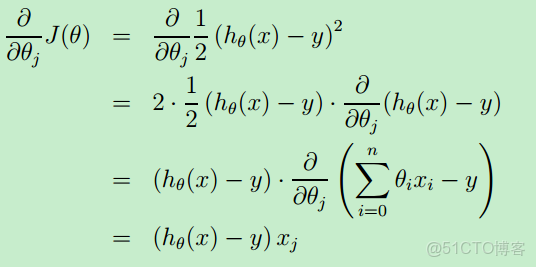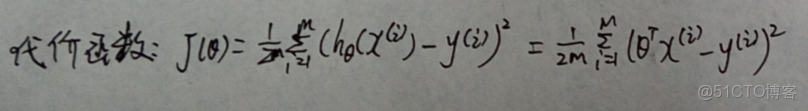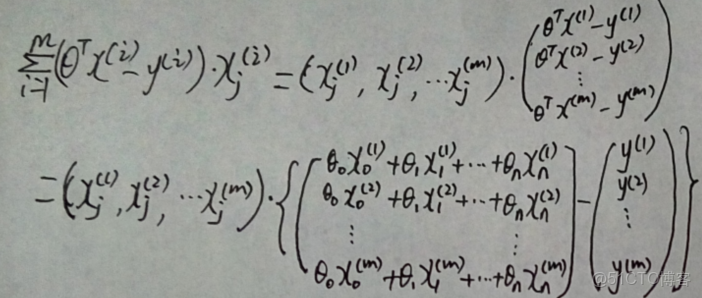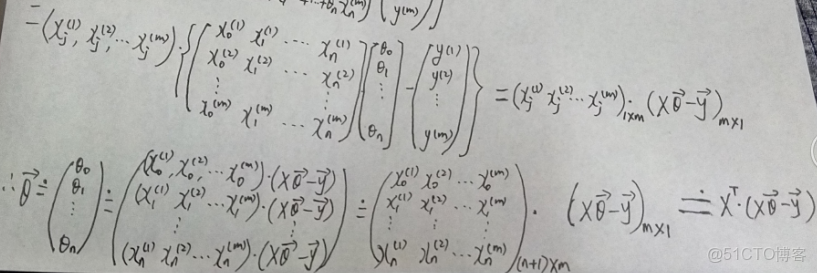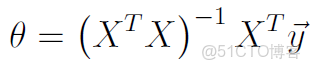①假設函數(hypothesis function)

在給定一些樣本數據(training set)後，採用某種學習算法(learning algorithm)對樣本數據進行訓練，得到了一個模型或者説是假設函數。

當需要預測新數據的結果時，將新數據作為假設函數的輸入，假設函數計算後得到結果，這個結果就作為預測值。

 

假設函數的表示形式一般如下：θ 稱為模型的參數(或者是：權重weights)，x就是輸入變量(input variables or feature variables)

 

可以看出，假設函數h(x)是關於x的函數，只要確定了 θ ，就求得了假設函數 (θ 也可視為一個向量)。那麼對於新的輸入樣本x，就可以預測該樣本的結果y了。

上面假設函數是從0到n求和，也就是説：對於每個輸入樣本x，將它看成一個向量，每個x中有n+1個 features。比如預測房價，那輸入的樣本 x(房子的大小，房子所在的城市，衞生間個數，陽台個數.....一系列的特徵)

 

關於分類問題和迴歸問題：假設函數的輸出結果y（predicted y）有兩種表示形式：離散的值和連續的值。比如本文中講到的預測利潤，這個結果就是屬於連續的值；再比如説根據歷史的天氣情況預測明天的天氣（下雨 or 不下雨），那預測的結果就是離散的值(discrete values)

因此，若hypothesis function輸出是連續的值，則稱這類學習問題為迴歸問題(regression problem)，若輸出是離散的值，則稱為分類問題(classification problem)

 

②代價函數(cost function)

學習過程就是確定假設函數的過程，或者説是：求出 θ 的過程。

現在先假設 θ 已經求出來了，就需要判斷求得的這個假設函數到底好不好？它與實際值的偏差是多少？因此，就用代價函數來評估。

 

向量化後的代價函數：

 

 

一般地，用 m 來表示訓練樣本的數目(size of training set)，x⁽ⁱ⁾ 表示第 i 個樣本，y⁽ⁱ⁾ 表示第i個樣本的預測結果。

從上圖可看出：代價函數與“最小均方差”的理念非常相似。J(θ)是 θ 函數。

顯然，“代價函數越小，模型就越好”。因此，目標就是：找到一組合適的 θ ，使得代價函數取最小值。

如果我們找到了 θ ，那不就求得了 假設函數了？也就求得一個模型--linear regression model.

那如何找 θ 呢？就是下面提到的梯度下降算法(gradient descent algorithm)

 

 

③梯度下降算法(Gradient descent algorithm)

 

梯度下降算法的本質就是求偏導數，令偏導數等於0，解出 θ

 

 

 

首先從一個初始 θ 開始，然後 for 循環執行上面公式，當偏導數等於0時，θ_j 就不會再更新了，此時就得到一個最終θ_j 值。

 

整個偏導數的運算過程如下：

 

 

 

④假設函數、代價函數和梯度下降算法的向量表示

 

假設函數的向量表示如下：

 

 

代價函數的表示如下：

 

 

使用梯度下降算法求解 θ 的向量化表示如下：

（原文上圖的式子有一處錯誤，第一個等號後的式子不應除以m，這裏加以更正了）

 

證明過程如下：

 

 

 

 

 

 

補充：

θ的閉式解（close-form solution）

θ的閉式解也就是它的解析解，就是使得代價函數J(θ)取得最小值的解；

使用閉式解的優點是一步得到精確解，避免了“loop until converge”；

缺點是當特徵數量較多時，X的維度較大，而求解的複雜度為O(n^3)，時間代價較高。（特徵數量一般以10^4為分界點，高於這個值一般考慮用梯度下降）