寫在前面的話:
hello~這一講主要內容是連續函數極限的求法,為求形式複雜的初等函數提供了依據。
有錯誤及時提出哦,我看到會糾正。
學習和思考讓我們的生活過得更有意義,雖然我們不是天才,但是我們所積累的一點一滴都會成就未來更好的自己!而且我相信,沒有所謂的天才,不要被那些“天才們“所嚇倒,通過努力,我們也會越來越接近他們。小夥伴們,我們一起加油吧~
一、連續函數和、差、積、商的連續性
定理1:有限個在某點連續的函數的和,是一個在該點連續的函數。
證明:設
都在
處連續,根據函數連續的定義,有
設
,則
故
在
處連續。
定理2:有限個在某點連續的函數的乘積是一個在該點連續的函數。
證明:設
都在
處連續,根據函數連續的定義,有
設
,則
故
在
處連續。
定理3:兩個在某點連續的函數的商是一個在該點連續的函數,只要分母在該點不為零。
證明:設
都在
處連續,根據函數連續的定義,有
設
,則
故
在
處連續。
這樣我們就知道:若函數
在點
處連續,則它們的和、差、積、商(只要分母在
處不為零)都在
處連續。
例1. 因
而
和
都在區間
內連續,故
在它們的
定義域內連續。
例2.
,分子分母皆為連續函數,所以整個商函數在分母不為零的情況下處處連續,即當
時,函數處處連續。
,分子分母皆為連續函數,所以商函數在分母不為零的情況下處處連續,即當
時處處連續。
二、反函數(戳我瞭解)和複合函數的連續性
定理4:如果函數
在區間
上單調增加(或單調減少)且連續),那麼它的反函數
也在對應的區間
上單調增加(或單調減少)且連續。
總之,單調連續的函數,它的反函數也是單調連續的。
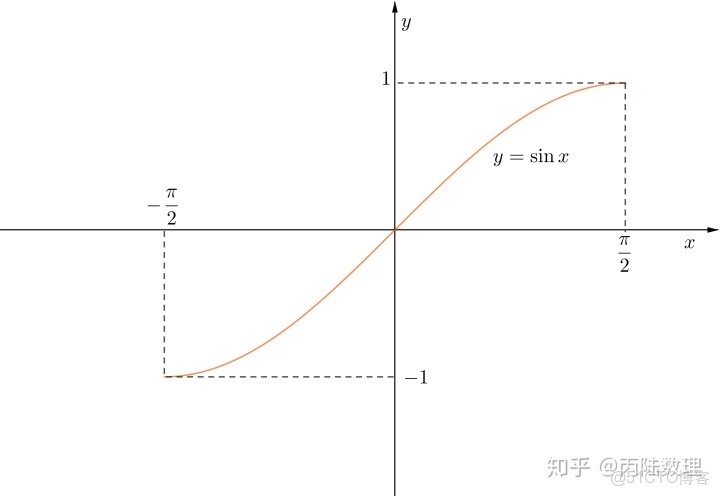
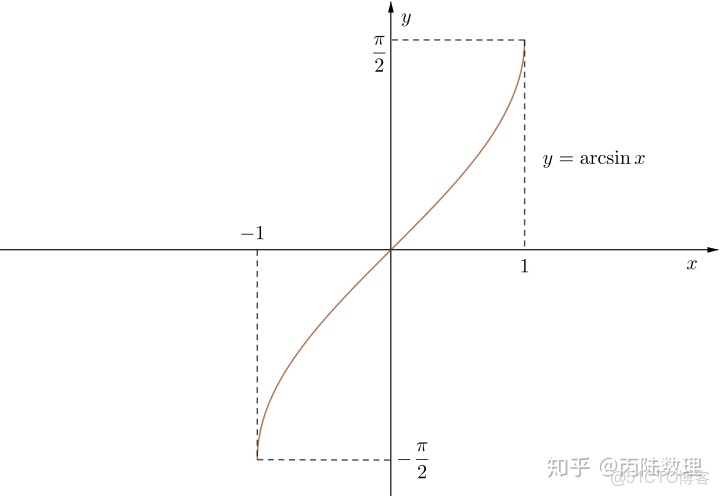
例3.由於
在閉區間
上單調增加且連續,所以它的反函數
在閉區間
上也是單調增加且連續的,如下圖:
同樣,
在閉區間
上單調減少且連續;
在
內單調增加且連續;
在區間
內單調減少且連續。
總之,反三角函數在它們的定義域內都是連續的。
定理5:設函數
當
時,極限存在且等於
,即
。而函數
在點
處連續,那麼複合函數
當
時極限存在且等於
,即
。(
簡言之,當
,裏層函數在有極限,外層函數連續,那麼,
)。
證明:對於外層函數
而言,因為
在
處連續,根據函數連續定義(戳我瞭解),有
① ,對①使用函數極限的定義:
,總存在
,使當
② 時,
。
對於內層函數
而言,
,由極限定義,對特給的
,必然也會
,
,有
,可見
滿足②式,故
,我們把帶有下劃線的文字連城一句:對任意給定的
,存在
,使當
,有
,這不就是函數極限的定義(戳我瞭解)嘛~,所以
。
知乎視頻www.zhihu.com
注:
- 在定理5中有 和 ,故定理5的結論又可寫成:
式表示,
在定理5的條件下,求複合函數極限
時,外層函數符的號
和極限符號可以
換序。
式表示,在定理5的條件下,如果做這樣一個變量替換
,那麼求
就可以轉化成
,此處
;
這兩個結論方便日後直接使用。
- 在定理5中,把 ,換成 ,仍有類似結論: ,不再證明。
例3.求
解:
可以看作
與
複合而成,而裏層函數
在
處有極限,即
,外層函數
,在
處連續,所以
。
定理6:設
,在
處連續,且
,而函數
在
處連續,那麼複合函數
在
點連續。(
簡言之,連續函數的複合函數也連續。)
證明:由於外層函數
在
處連續,即
,根據極限定義,
,有
,當
時,
。
由於內層函數
在
處連續,即
,根據極限定義,對剛剛得到的
,必然也
,
(而這又對應於上部分證明過程中
時,
),所以,
。
我們把帶有下劃線的文字連成一句,即為極限定義,即
(函數在
處極限值等於在該點的函數值),所以複合函數
在
點連續。
例4.討論函數
的連續性。
解:函數
可看作由
和
複合而成。
在
是連續的,
在
是處處連續的,所以複合函數
在
是連續的。
三、初等函數的連續性
前面證明了三角函數和反三角函數在定義域內是連續的,同樣可以證明
在
是連續的。
由於
在
是單調連續的,而它的值域是
,由定理4可知,它的反函數對數函數
在區間
內單調且連續。
冪函數
的定義域因
而異,但不論
為何值,冪函數在
內是有定義的,下面證明冪函數在
內是連續的。事實上,當
時,
即函數可以看成
和
複合而成,由定理6,它在
內連續。
綜上,基本初等函數在它們的定義域內是連續的。由於初等函數是由基本初等函數經過有限次四則運算或複合運算而來,而連續函數的和、差、積、商以及複合函數都是連續函數,因此初等函數在定義域內連續。
初等函數的連續性為求極限提供了有效的方法(欲求某點的極限值只需求該點的函數值):如果
是初等函數,
為其定義域內的一點,則
極限值等於函數值:
。例如:
是初等函數
的定義域
內的一點,所以
。下面再看幾個初等函數求極限的例子:
例5.求
解:
例6.
解:
例7.
解:
例8.
解:
例9.
解:
例10.
解:
例11.
解: