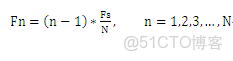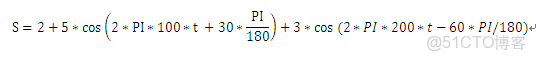假設信號的採樣頻率是Fs，信號的頻率是F，採樣點數為N，則與傅里葉變換相關概念幾個計算公式如下：

1.      頻率計算公式

                                                                   

振動幅值數據分析_採樣率

                                        

2.      振幅計算公式 Magnitude

                

振動幅值數據分析_振動幅值數據分析_02

     


3.       相位計算公式Pan


                          

振動幅值數據分析_採樣率_03

 

 

示例：假設有如下兩個交流信號，以512的採樣率對信號進行採樣，採樣點數也為512點。

     信號1:  2V的直流分量，幅度為5V，頻率為100hz，相位為30度。

     信號2：幅度為3V，頻率為200hz，相位為-60度。

用數學表達式來描述如下：

                                               

振動幅值數據分析_採樣率_04

               

下面的matlab腳本畫出其頻譜圖：

>>N_data_size = 512;
>> t = [0:1:N_data_size];
>> fs = 512;
>> t = t/fs;
>> s = 2 + 5 * cos(2 * pi * 100 * t +30 * pi / 180) + 3 * cos(2 * pi * 200 * t-60 * pi / 180);
>> M = abs(fft(s,N_data_size));
>> plot(M);

                              

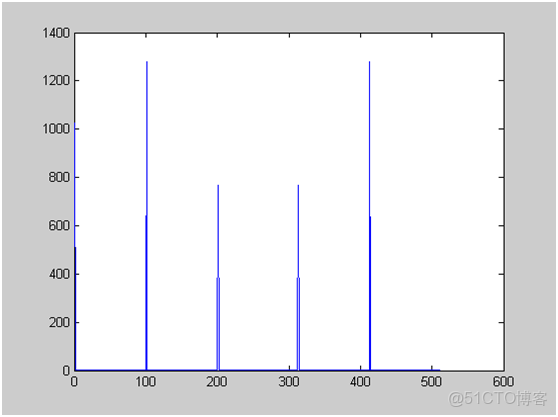
振動幅值數據分析_採樣頻率_05


                                   

 

 

因採樣點數等於採樣頻率，因此兩個點之間的頻率間隔是1Hz。按照頻率計算公式Fn=(n-1)*FS/N計算，第n個點的頻率就是n-1.因此第101個點的頻譜就是100，對應於原始信號第一個交流信號的頻率，第201個點的頻率是200，對應於第二個交流信號的頻率。由此可知，圖像應該在第0,101,201三個點上出現峯值。從上面的圖看，確實是這樣。注意，頻譜圖關於奈奎斯特頻率是對稱的，所以只看奎斯特頻率以下的部分就可以了。

 

根據前面的公式，第一個點的模值為直流分量*N = 2 *512 = 1024；

第一個原始信號的峯值為A =5，因此它的模值為 A * N/2= 5 * 512/2 = 1280;

第二個原始信號的峯值為A=3，因此它的模值為 A * N/2 =3 * 512/2 = 768;

 

分別拿出這三個點的FFT結果來細看：

第一個點的FFT結果： 1024 + 0* i , A1 = sqrt(1024*1024) = 1024;

第二個點的FFT結果：1108.5+640*I,A101 = sqrt(1108.5*1108.5+640*640) = 1280;

第三個點的FFT結果：384-665.11i,A201= sqrt(384*384+665.11*665.11) = 768;

 

由此可見，如果知道了每個頻率點信號的峯值和採樣點數，那麼很容易計算出它的模值。反過來也是如此，即如果用FFT計算出了信號的模值，也很容易計算出原始信號的峯值。例如，對於上例：直流分量的值：A= A1/N = 1024/512 = 2;

交流信號1的幅度為：A =A101/N/2=1280*2/512=5;

交流信號2的幅度為：A=A201/N/2=768*2/512=3.


相位的計算就更簡單，從略。