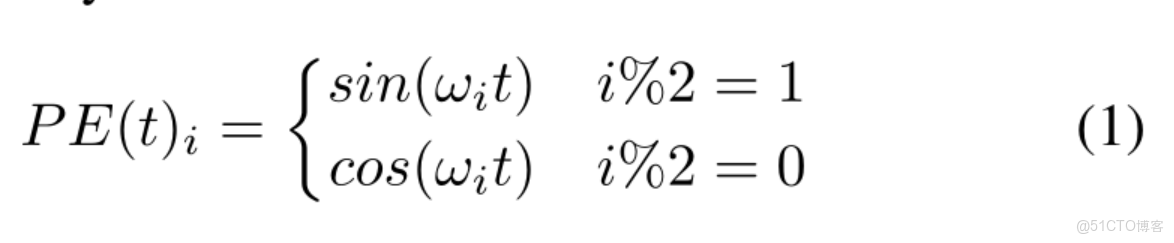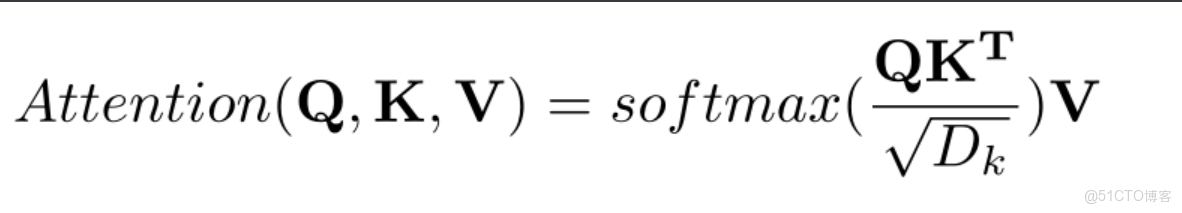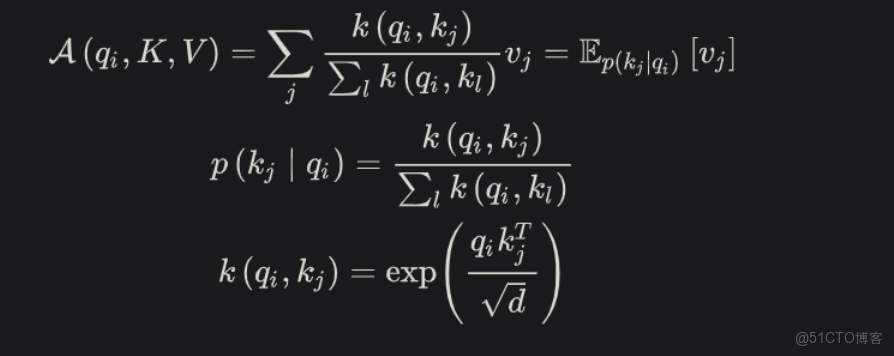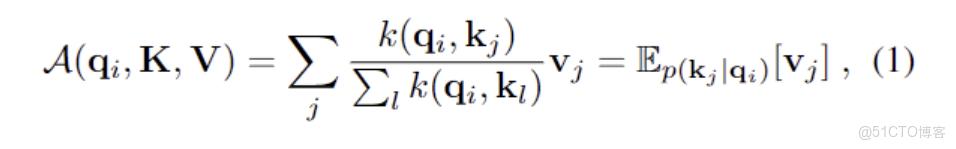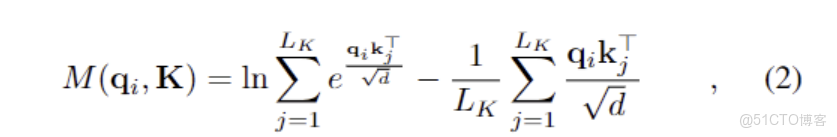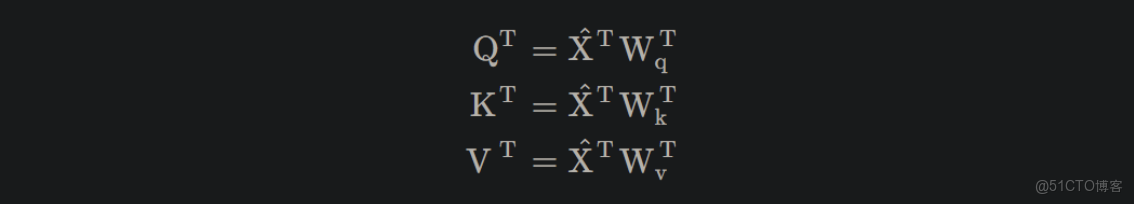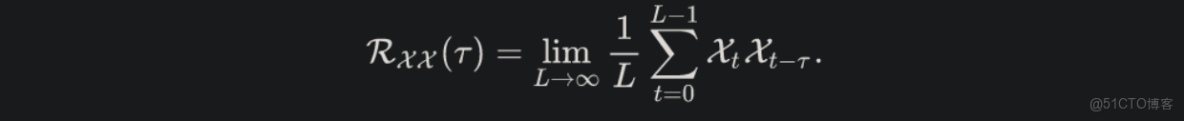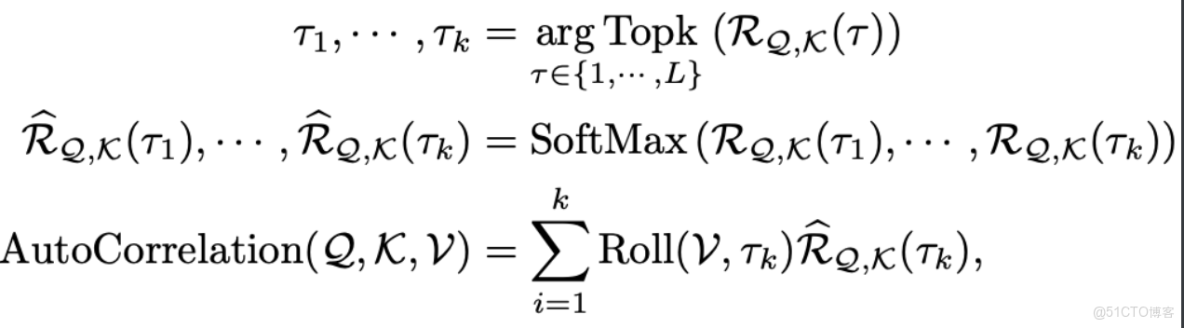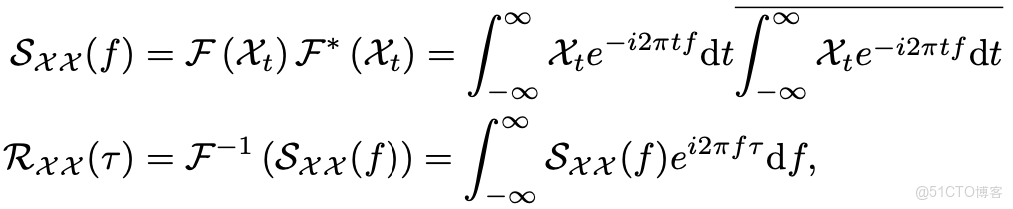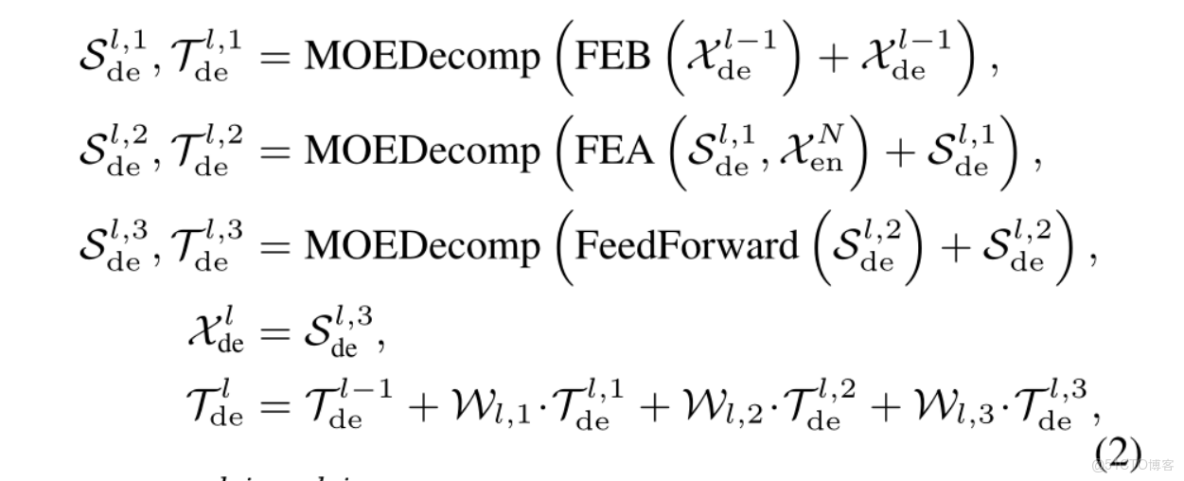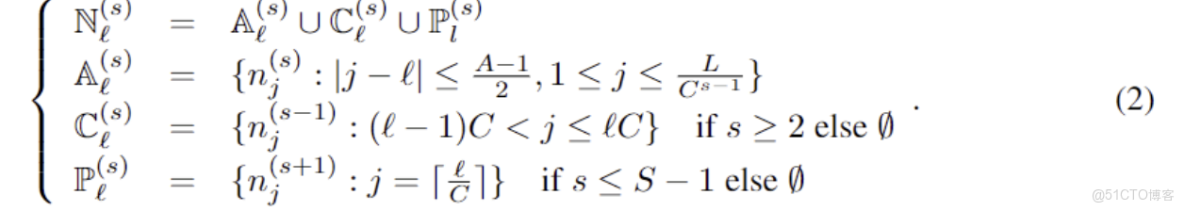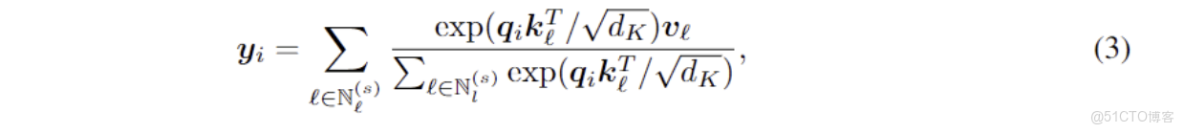Transformer的時間序列預測

1、它利用輸入嵌入中添加的位置編碼來模擬序列信息。（位置編碼）

絕對位置編碼：

t表示位置索引，w為每個維度的頻率信息

相對位置編碼：根據輸入元素之間的成對位置關係比元素的位置更有利的直覺，相對位置編碼方法已經被提出。例如，其中一種方法是將可學習的相對位置嵌入到注意力機制的關鍵中

混合位置編碼：將兩種方法結合起來。位置編碼被添加到標記嵌入中，並送入轉化器

2、注意力機制

2.1Attnention原理

在對於各時序點數據重視程度是一樣的，而注意力機制在Decoder端使用針對不同解碼值使用不同中間語義表示向量Ci，可理解為，在解碼器計算相應yi時，使用不同針對編碼器不同中間語義值Ci

Attnetion主要使用由三個部分組成：

第一個是Query，可視作時序數據中每個詞向量對應的查詢向量，其所構成的張量維度為[batch size, Target sequence length, (h, 使用多頭方法時的多頭數目), hidden embedding dimension (/h, 使用多頭時應除以多頭數目]；

第二個是Key，可視作時序數據中每個詞向量對應的鍵值向量，其所構成的張量維度為[batch size, Source sequence length, (h, 使用多頭時多頭數目), hidden embedding dimension (h, 使用多頭時應除以多頭數目]，Key與各詞向量對應的鍵向量相乘後再進行softmax可以得到注意權重值。

第三個是Value，可視作時序數據中每個詞向量對應的隱藏信息，其所構成的張量維度為[batch size, Source sequence length, (h, 使用多頭時多頭數目), Output embedding dimension (h, 使用多頭時應除以多頭數目]。

縮放點乘法注意力

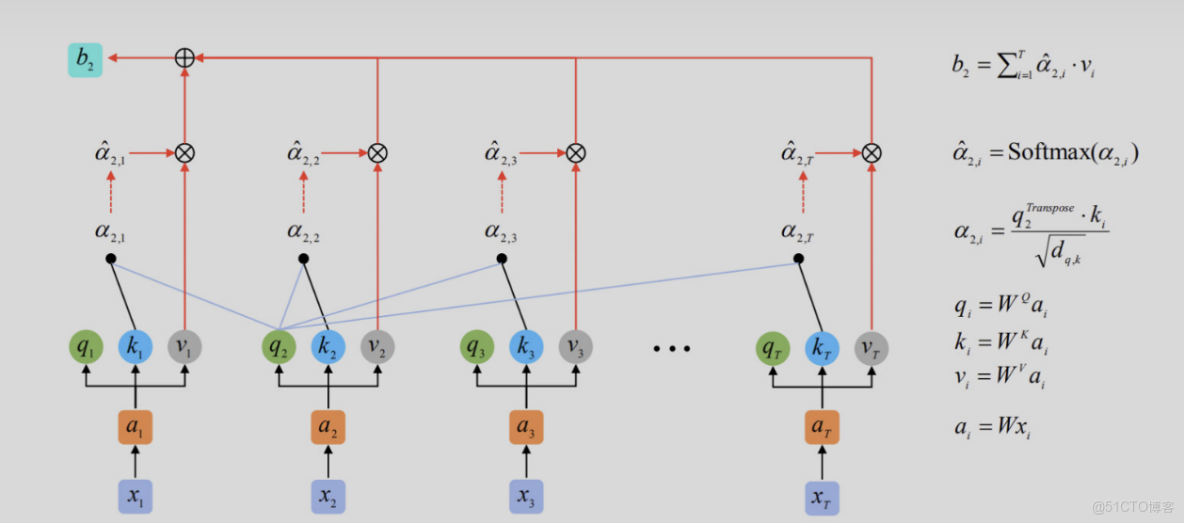
因此Attention的計算步驟主要有兩步：1、求權重係數2、求Attention 的值

1、根據當前Query與各Key計算得到相關性評價值，得到一階的相關程度值矩陣，其中通常評價相關性值的方法主要有三種，一是求兩個向量點積；二是求cos的相似性；三是利用神經網絡求解；四是加和等方法

再對矩陣中的各值進行歸一化處理，得到各Value對應的注意力權重值a，通常採用Softmax方法。

2、用注意力權重a與Source中的Value進行加權求和，得出注意力值Attention。

具體算例如下：

設Query為M ×d，其中M為Source時序數據長，Key為為N ×d，其中N為Target時序數據長，d為向量維度。可見，向量Q與K是等長的，因為兩者應在同一個維度空間中，需要進行相似度比較，即dQ = dK= d。但V為N ×dv，其向量長度可與兩者不同，可以認為K與V的鍵值對是在不同狀態空間中對同一數據的表示，最終Attention值為M ×dv的矩陣，使用Softmax加權後得到權重係數，依據係數在dv個維度上進行加權求和，最終得出M個具有dv維度的Attention值。

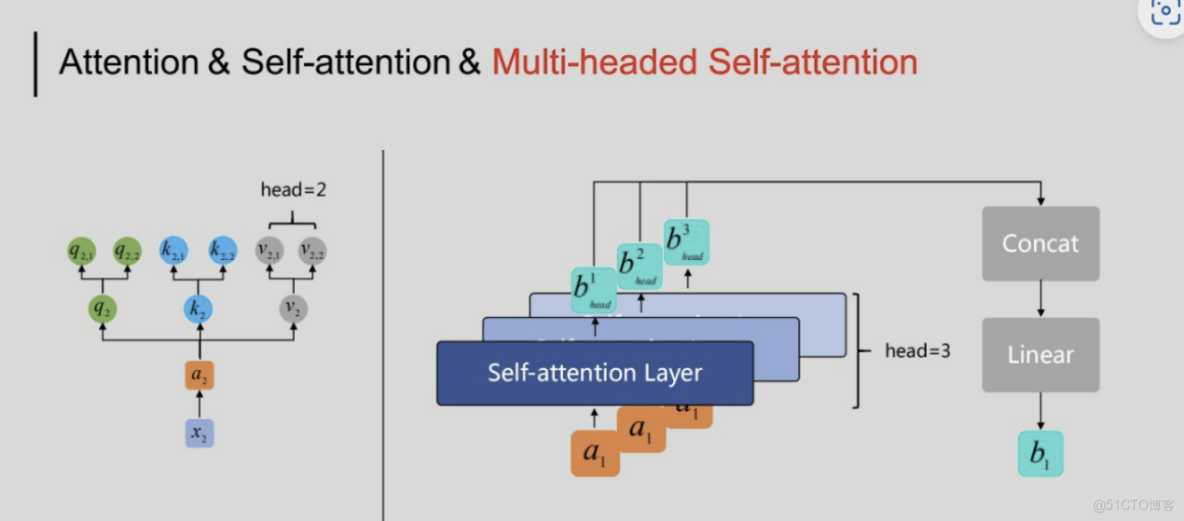
2.2多頭注意力

Attention是將query和key映射到同一高維空間中去計算相似度，而對應的multi-head attention把query和key映射到高維空間的不同子空間中去計算相似度

2.3自注意力

跳脱出了Source與Target的框架，而是尋找Source或Target內部的注意力機制。Self-Attention中的Q、K、V均為相同輸入，其計算方式仍與Attention方法相同，encoder中的self-attention的query, key, value都對應了源端序列(即A和B是同一序列)，decoder中的self-attention的query, key, value都對應了目標端序列

通過計算Self-Attention，可以分析時序數據中內部信息的關係

舉例：求解得到句子中各單詞對當前解碼單詞的貢獻程度，可以表示一個句子中每個單詞之間的依賴關係。時間序列預測中採用給注意力機制

2.4 時序預測中的注意力機制

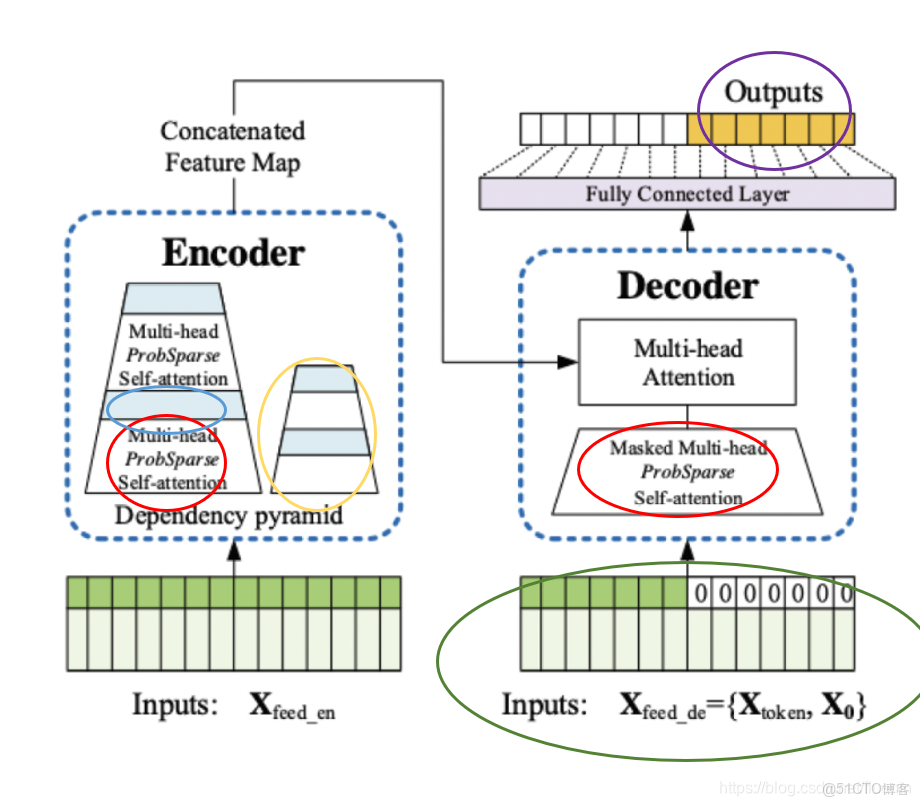
2.4.1 informer概率稀疏注意力

（KL散度進行注意力區分，通過關注TOP-U個佔據主導位置的query來實現）

論文標題：Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting

論文鏈接：https://arxiv.org/abs/2012.07436

代碼鏈接：https://github.com/zhouhaoyi/Informer2020

論文來源：AAAI 2021

Transformer在長距離依賴的表達方面表現出了較高的潛力。然而，Transformer存在幾個嚴重的問題，使其不能直接適用於LSTF問題，例如、高內存使用量和編碼器-解碼器體系結構固有的侷限性。其中Transformer模型主要存在下面三個問題：

1. self-attention機制的二次計算複雜度問題：self-attention機制的點積操作使每層的時間複雜度和內存使用量為 。
2. 高內存使用量問題：對長序列輸入進行堆疊時，J個encoder-decoder層的堆棧使總內存使用量為 ，這限制了模型在接收長序列輸入時的可伸縮性。
3. 預測長期輸出的效率問題：Transformer的動態解碼過程，使得輸出變為一個接一個的輸出，後面的輸出依賴前面一個時間步的預測結果，這樣會導致推理非常慢。

主要是為解決self-attention機制的過度使用採用概率稀疏的注意力來替代，

ProbSparse Self-attention 輸入： 32 × 8 × 96 × 64 (8×64=512 ,這也是多頭的原理，即8個頭) 輸出：32 × 8 × 25 × 64

我們回顧了傳統的注意力機制，引入了注意力概率矩陣，下面直接進入到最精彩的部分——ProbSparse的注意力機制。

對原始的注意力機制進行改寫，進行一步對注意力進行區分：分為Activate-lazy 兩種，通過KL散度（信息熵來劃分兩種注意力），利用建立的度量標準，通過TOP-U個佔據主導地位的query，最終實現概率稀疏注意力（實際上也是比較合理的，因為某個元素可能之和幾個元素高度相關，其他的並無顯著關聯）。基於這樣的結果，引入了attention:

主要公式為：

2.4.2 STTNs動態空間注意力

(聯合利用動態的定向空間依賴和長距離的時間依賴來提高長期交通流預測的準確性。我們提出了一種新的圖神經網絡變體，名為空間Transformer，以動態的方式建立具有自注意力機制的有向空間依賴關係模型，以捕捉交通流的實時狀況和方向)

論文標題：Spatial-Temporal Transformer Networks for Traffic Flow Forecasting

論文鏈接：[2207.05064] 用於交通流量預測的自適應圖時空變壓器網絡 (arxiv.org)

代碼鏈接：https://github.com/xumingxingsjtu/STTN

論文來源：ICDM, 2021

1. 交通流具有高度的非線性和動態的時空相關性，如何實現及時準確的交通預測，特別是長期的交通預測仍然是一個開放性的挑戰
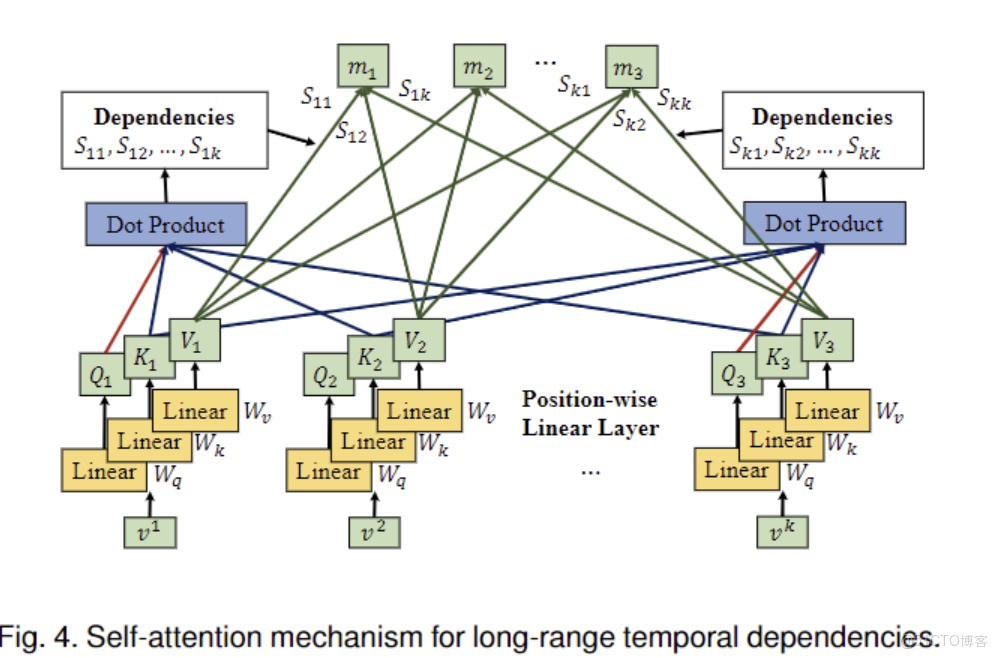
2. 提出了一種新的Spatio-Temporal Transformer Network(STTNs)範式，該範式聯合使用 dynamical directed spatial dependencies和long-range temporal dependencies來提高長期交通流預測的準確性。
3. Spatial transformer利用self-attention對有向空間依賴關係進行動態建模，以捕獲交通流的實時狀態和方向。並且考慮了相似性、連通性和協方差等多種因素,採用multi-head attention 對空間依賴關係進行聯合建模。此外，temporal transformer被開發用於建模long-range雙向時間依賴。與現有的工作相比，STTNs能夠對長期的空間-時間依賴關係進行高效和可擴展的訓練。
4. 實驗結果表明，在真實的PeMS-Bay和PeMSD7(M)數據集上，STTNs具有與當前技術水平相當的競爭力，特別是在長期交通流量預測方面。

一個節點的未來交通狀況是由其鄰近節點的交通狀況、觀測的時間步長以及交通事故、天氣狀況等突變決定的。在本節中，我們開發了一個ST blocks來整合空間和時間的transformer，以聯合建模交通網絡中的空間和時間依賴性，以精確預測 將spatial transformer S和temporal transformer T 疊加生成3D輸出張量。採用剩餘連接進行穩定訓練。在第l ll個時空塊中，spatial transformer S 和圖鄰接矩陣A AA中提取空間特徵自注意力機制來模擬時間上的依賴性。時間Transformer的輸入是一個時間序列 

2.4.3 Autoformer自相關機制

（基於隨機過程理論，對離散的時間過程{tx},並對其計算自相關係數，並藉助快速傅里葉變換）

論文標題：Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting

論文鏈接：[2106.13008] 自成型器：用於長期串聯預測的自相關分解變壓器 (arxiv.org)

代碼鏈接：https://github.com/thuml/autoformer

論文來源：NeurIPS 2021.

提出了名為Autoformer的模型，主要包含以下創新：

• 突破將序列分解作為預處理的傳統方法，提出深度分解架構（Decomposition Architecture），能夠從複雜時間模式中分解出可預測性更強的組分。
• 基於隨機過程理論，提出自相關機制（Auto-Correlation Mechanism），代替點向連接的注意力機制，實現序列級（series-wise）連接和O(Llog⁡L)複雜度，打破信息利用瓶頸。

自相關機制： 基於隨機過程理論，通過離散的時間過程，來計算自相關係數。不同週期的相似相位之間通常表現出相似的子過程，我們利用這種序列固有的週期性來設計自相關機制，其中，包含基於週期的依賴發現（Period-based dependencies）和時延信息聚合（Time delay aggregation）。實現高效的序列級連接，從而擴展信息效用

具體過程和主要公式：

自相關係數表示序列與它的延遲之間的相似性。我們將這種時延相似性看作未歸一化的週期估計的置信度，即週期長度為T的置信度為R（T）。

時延信息聚合： 為了實現序列級連接，我們需要將相似的子序列信息進行聚合。我們這裏依據估計出的週期長度，首先使用Roll()操作進行信息對齊，再進行信息聚合，我們這裏依然使用query、key、value的形式，從而可以無縫替代自注意力機制

自相關係數RXX(τ)可以使用快速傅立葉變換（FFT）得到，計算過程如下：

其中，F和F−1分別表示FFT和其逆變換。因此，自相關機制的複雜度為O(Llog⁡L)。相比於之前的注意力機制或者稀疏注意力機制，自注意力機制（Auto-Correlation Mechanism）實現了序列級的高效連接，從而可以更好的進行信息聚合，打破了信息利用瓶頸。

2.4.4 FEDformer頻域增強注意力

（一般信號在頻域上具有稀疏性，也就是説，在頻域上只需保留很少的點，就能幾乎無損的還原出時域信號。保留的點越多，信息損失越少，反之亦然。雖然無法直接理論證明在頻域上應用各種神經網絡結構能夠得到更強的表徵能力。但在實驗中發現，引入頻域信息可以提高模型的效果，）

論文標題：FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting

論文鏈接：[2201.12740] FEDformer：用於長期串聯預測的頻率增強型分解變壓器 (arxiv.org)

代碼鏈接：https://github.com/MAZiqing/FEDformer

論文來源：ICML 2022

在Auttoformer的基礎上添加了小波增強和頻域變換，

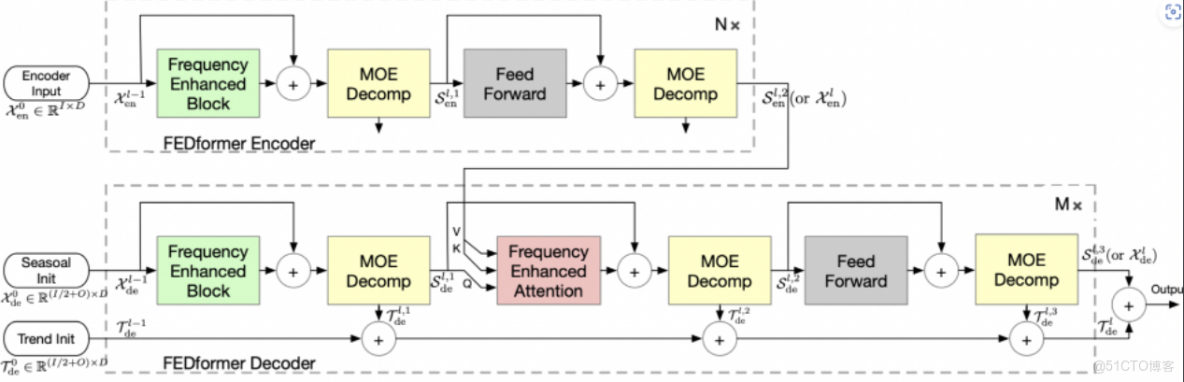
FEDformer 中兩個最主要的結構單元的設計靈感正是來源於此。Frequency Enchanced Block（FEB）和 Frequency Enhanced Attention（FEA）具有相同的流程：頻域投影 -> 採樣 -> 學習 -> 頻域補全 -> 投影回時域：

整體架構：

1. 首先將原始時域上的輸入序列投影到頻域。
2. 再在頻域上進行隨機採樣。這樣做的好處在於極大地降低了輸入向量的長度進而降低了計算複雜度，然而這種採樣對輸入的信息一定是有損的。但實驗證明，這種損失對最終的精度影響不大。因為一般信號在頻域上相對時域更加“稀疏”。且在高頻部分的大量信息是所謂“噪音”，這些“噪音”在時間序列預測問題上往往是可以捨棄的，因為“噪音”往往代表隨機產生的部分因而無法預測。相比之下，在圖像領域，高頻部分的“噪音”可能代表的是圖片細節反而不能忽略。
3. 在學習階段，FEB採用一個全聯接層 R 作為可學習的參數。而 FEA 則將來自編碼器和解碼器的
4. 信號進行cross-attention操作，以達到將兩部分信號的內在關係進行學習的目的。
5. 頻域補全過程與第2步頻域採樣相對，為了使得信號能夠還原回原始的長度，需要對第2步採樣未被採到的頻率點補零。
6. 投影回時域，因為第4步的補全操作，投影回頻域的信號和之前的輸入信號維度完全一致。

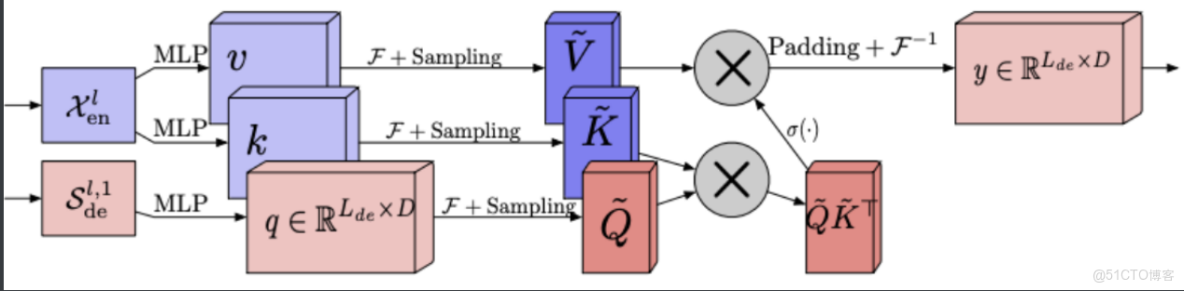
頻域增強注意力：

傳統Transformer中採用的Attention機制是平方複雜度，而 Frequency Enhanced Attention（FEA）中採用的Attention是線性複雜度，這極大提高了計算效率。因為 FEA 在頻域上進行了採樣操作，也就是説：“無論多長的信號輸入，模型只需要在頻域保留極少的點，就可以恢復大部分的信息”。採樣後得到的小矩陣，是對原矩陣的低秩近似。作者對 低秩近似與信息損失的關係進行了研究，並通過理論證明，在頻域隨機採樣的低秩近似法造成的信息損失不會超過一個明確的上界。證明過程較為複雜，有興趣的讀者請參考原文。

傅立葉基和小波基均基於傅立葉變換進行介紹，同理，小波變換也具有相似的性質，因而可以作為FEDformer的一個變種。傅立葉基具有全局性而小波基具有局部性。作者通過實驗證明，小波版的FEDformer可以在更復雜的數據集上得到更優的效果。但小波版的FEDformer運行時間也會更長。

主要公式：

2.4.5 PYformer金字塔注意力

論文標題：Pyraformer:Low-complexity pyramidal attention for long-range time seriesmodeling and forecasting

論文鏈接：吡喃反應器：用於長程時間序列建模和預測的低複雜度金字塔關注|打開審閲 (openreview.net)

代碼鏈接：支付寶/吡拉福 (github.com)

論文來源：ICLR 2022

解決問題：

1）緊湊地捕獲不同範圍的時間依賴性 ，包括長期和短期預測

2）簡潔的模型以及更低的計算消耗。 值得注意的是處理遠程依賴中更困難的任務（可以類比長期預測），其特點是在時間序列中任意兩個時間節點最長的信號遍歷路徑的長度，路徑越短，捕捉的關鍵依賴就越好（注意力權重越高）

總結一下該論文的主要貢獻：

1、提出基於多分辨率表示的Pyraformer來捕捉時間序列多個範圍下的時間關聯，統計Pyraformer和先進方法視圖，並比較了複雜度和最長信號遍歷路徑的長度。 2、理論上，通過合理地調整相應超參，實現O(1)的最大路徑長度和O ( L )的時間與空間複雜度。 3、提出的Pyraformer在多個真實數據集上的單步時間序列預測和多步時間序列預測性能要好過原始Transformer及其變體，並且消耗的時間和內存更少。

文章對已有的tansformer模型簡單的梳理：

稀疏Transformer該部分主要是統計一下已經被提出的稀疏Transformer，比如LongTransformer、Reformer、ETC。

LongTransformer採用與CNN類似的局部窗口，將複雜度降低到O(AL)，其中 A 是局部窗口大小，但有限的窗口大小使得全局交換信息變得困難。 Reformer利用局部敏感哈希 (LSH) 將序列劃分為幾個bucket，Reformer的最大路徑長度與bucket的數量成正比，更糟糕的是，需要很大的bucket來降低複雜度 ，ETC設計的全局token數目為G，通常會隨着L的增加而增加，並且隨之而來的複雜度仍然是超線性的。

層次Transformer簡要回顧提高 Transformer 捕獲自然語言層次結構的能力的方法，重點有兩個：Multi-scale Transformer和BP-Transformer。

Multi-scale Transformer 使用自上而下和自下而上的網絡結構學習序列數據的多尺度表示，可以適當地減少原始Transformer的複雜度，但還是陷入L^2的複雜度。 BP-Transformer遞歸地將整個輸入序列劃分為兩個，直到最後一個分區只包含一個標記。然後，分割後的序列形成一棵二叉樹，與圖密切相關。Pyraformer也是形成一棵樹。與 Pyraformer 相比，BP-Transformer 與更密集的圖相關聯，因此導致O(Llog(L))的更高複雜度。

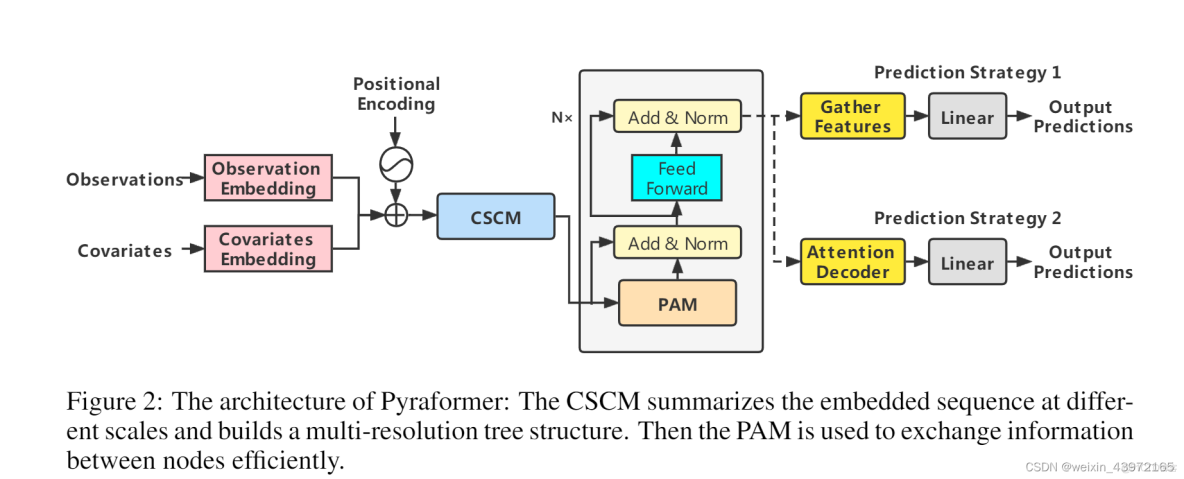
整體架構圖：

具體運行流程為：首先，將輸入的歷史觀測值嵌入特徵、全局時間協變量嵌入特徵、位置編碼相加在一起，與長程時間序列預測模型Informer的做法是一樣的。然後，構建多分辨率的卷積模塊，利用細尺度下的原始序列節點生成較粗尺度下的父節點，父節點的數目是子節點的C倍，最終形成細尺度和較粗尺度的CC叉樹，較粗尺度的節點匯聚了上一層子節點的特徵信息。為了進一步地捕捉不同範圍下的時間依賴，將CSCM生成的粗細度時間節點特徵傳入金字塔注意力模塊，基於注意力機制進行節點尺度間和尺度內的信息傳遞。最後，針對單步預測和多步預測，採用不同的預測方法來預測結果。

金字塔注意力模塊（PAM）：

可以將金字塔圖分解為兩部分：尺度間和尺度內連接。尺度間連接將金字塔圖的最細尺度與原始時間序列的每小時觀測值相關聯，則較粗尺度上的節點可以視為時間序列的每日、每週甚至每月特徵。尺度內連接將每層尺度的鄰居節點連接起來。較粗尺度相比較細尺度更適合描述長期相關性。

並將原有的attention變換為