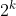在計算機科學中，k-d樹（k-dimensional的縮寫）是一種空間劃分數據結構，用於組織k維空間中的點。主要應用於多維空間關鍵數據的搜索（如：範圍搜索和最近鄰搜索）。k-d樹是空間二分樹（Binary space partitioning ）的一種特殊情況。

索引結構中相似性查詢有兩種基本的方式：

• 一種是範圍查詢（range searches）：範圍查詢就是給定查詢點和查詢距離的閾值，從數據集中找出所有與查詢點距離小於閾值的數據；
• 另一種是K近鄰查詢（K-neighbor searches）：K近鄰查詢是給定查詢點及正整數K，從數據集中找到距離查詢點最近的K個數據，當K=1時，就是最近鄰查詢（nearest neighbor searches）。

特徵匹配算子大致可以分為兩類：

• 一類是線性掃描法，即將數據集中的點與查詢點逐一進行距離比較，也就是窮舉，缺點很明顯，就是沒有利用數據集本身藴含的任何結構信息，搜索效率較低。
• 第二類是建立數據索引，然後再進行快速匹配。因為實際數據一般都會呈現出簇狀的聚類形態，通過設計有效的索引結構可以大大加快檢索的速度。索引樹屬於第二類，其基本思想就是對搜索空間進行層次劃分。根據劃分的空間是否有混疊可以分為Clipping和Overlapping兩種。前者劃分空間沒有重疊，其代表就是k-d樹；後者劃分空間相互有交疊，其代表為R樹。

高維數據

維數災難讓大部分的搜索算法在高維情況下都顯得花哨且不實用。 同樣的，在高維空間中，k-d樹葉並不能做很高效的最鄰近搜索。一般的準則是：在k維情況下，數據點數目N應當遠遠大於

時，k-d樹的最鄰近搜索才可以很好的發揮其作用。

k-d樹是每個節點都為k維點的二叉樹。所有非葉子節點可以視作用一個超平面把空間分割成兩個半空間。節點左邊的子樹代表在超平面左邊的點，節點右邊的子樹代表在超平面右邊的點。選擇超平面的方法如下：每個節點都與k維中垂直於超平面的那一維有關。因此，如果選擇按照x軸劃分，所有x值小於指定值的節點都會出現在左子樹，所有x值大於指定值的節點都會出現在右子樹。這樣，超平面可以用該x值來確定，其法線為x軸的單位向量。

創建k-d樹

構建k-d樹是一個逐級展開的遞歸過程。

有很多種方法可以選擇軸垂直分割面（ axis-aligned splitting planes ），所以有很多種創建k-d樹的方法。 最典型的方法如下：

• 隨着樹的深度輪流選擇軸當作分割面。（例如：在三維空間中根節點是 x 軸垂直分割面，其子節點皆為 y 軸垂直分割面，其孫節點皆為 z 軸垂直分割面，其曾孫節點則皆為 x 軸垂直分割面，依此類推。）
• 點由垂直分割面之軸座標的中位數區分並放入子樹

選擇軸垂直分割面，對於所有描述子數據（特徵矢量），統計它們在每個維上的數據方差：數據方差大表明沿該座標軸方向上的數據分散得比較開，在這個方向上進行數據分割有較好的分辨率。

這個方法產生一個平衡的k-d樹。每個葉節點的高度都十分接近。然而，平衡的樹不一定對每個應用都是最佳的。 [2] 

查找：最鄰近搜索

最鄰近搜索用來找出在樹中與輸入點最接近的點。

k-d樹最鄰近搜索的過程如下：

1. 從根節點開始，遞歸的往下移。往左還是往右的決定方法與插入元素的方法一樣(如果輸入點在分區面的左邊則進入左子節點，在右邊則進入右子節點)。
2. 一旦移動到葉節點，將該節點當作"當前最佳點"。
3. 解開遞歸，並對每個經過的節點運行下列步驟：

1. 如果當前所在點比當前最佳點更靠近輸入點，則將其變為當前最佳點。
2. 檢查另一邊子樹有沒有更近的點，如果有則從該節點往下找。

4. 當根節點搜索完畢後完成最鄰近搜索。

實例：搜索過程

在k-d樹中進行數據的查找也是特徵匹配的重要環節，其目的是檢索在k-d樹中與查詢點距離最近的數據點。這裏先以一個簡單的實例來描述最鄰近查找的基本思路。

1. 例1：簡單

星號表示要查詢的點（2.1,3.1）。通過二叉搜索，順着搜索路徑很快就能找到最鄰近的近似點，也就是葉子節點（2,3）。而找到的葉子節點並不一定就是最鄰近的，最鄰近肯定距離查詢點更近，應該位於以查詢點為圓心且通過葉子節點的圓域內。

為了找到真正的最近鄰，還需要進行'回溯'操作：算法沿搜索路徑反向查找是否有距離查詢點更近的數據點。

第一步，二叉查找：自上而下，與超平面進行比較，判斷進入左子樹還是右子樹，形成搜索路徑。

此例中先從(7, 2)點開始進行二叉查找，超平面為x=7，2.1< 7，所以進入左子樹到達(5,4)；此時超平面為y=4，3.1<4，所以到達(2,3)，此時搜索路徑中的節點為<(7, 2)，(5, 4)，(2, 3)>；

第二步，找到最近鄰點：首先以(2, 3)作為當前最近鄰點；

第三步，回溯：自下而上，檢查以查詢點為中心、最近鄰點距離為半徑的圓是否與父節點的超平面相交

以(2, 3)點開始，計算其到查詢點(2.1,3.1)的距離為0.1414，然後回溯到其父節點(5, 4)，判斷在該父節點的其他子節點空間中是否有距離查詢點更近的數據點。即，以(2.1,3.1)為圓心，以0.1414為半徑畫圓，如圖4所示，發現該圓並不和超平面y = 4交割，因此不用進入(5,4)節點右子空間中去搜索。

                                                     

再回溯到(7, 2)，以(2.1, 3.1)為圓心，以0.1414為半徑的圓更不會與x = 7超平面交割，因此不用進入(7, 2)右子空間進行查找。至此，搜索路徑中的節點已經全部回溯完，結束整個搜索，返回最近鄰點(2, 3)，最近距離為0.1414。

2. 例2：一個複雜點的例子如查找點為(2, 4.5)

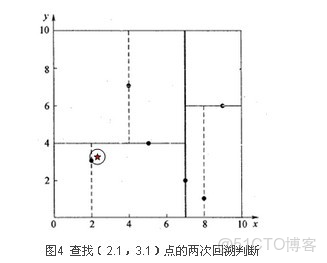
第一步，同樣先進行二叉查找，先從(7, 2)查找到(5, 4)節點，在進行查找時是由y = 4為分割超平面的，由於查找點為y值為4.5，因此進入右子空間查找到(4, 7)，形成搜索路徑<(7, 2)，(5, 4)，(4, 7)>;

第二步，取(4, 7)為當前最近鄰點，計算其與目標查找點的距離為3.202。

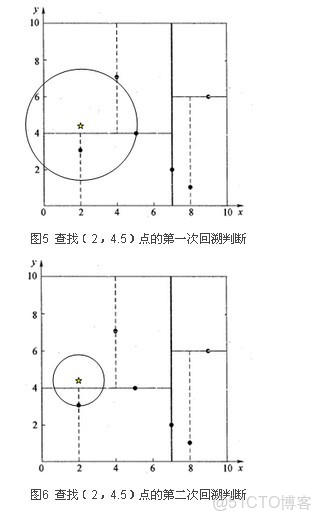
第三步，回溯，以(4, 7)點開始，計算其與查找點之間的距離為3.202。回溯到父節點(5, 4)，以(2, 4.5)為圓心，以3.202為半徑作圓，如圖5所示（圖中有誤），可見該圓和y = 4超平面交割，所以需要進入(5, 4)左子空間進行查找。此時需將(2, 3)節點加入搜索路徑中得<(7, 2)，(2, 3)>。回溯至(2, 3)葉子節點，(2, 3)距離(2, 4.5)比(5, 4)要近，所以最近鄰點更新為(2, 3)，最近距離更新為1.5。回溯至(7, 2)，以(2, 4.5)為圓心1.5為半徑作圓，並不和x = 7分割超平面交割，如圖6所示。至此，搜索路徑回溯完。返回最近鄰點(2, 3)，最近距離1.5。k-d樹查詢算法的偽代碼如下所示。

                                   

步驟總結：

1. 從root節點開始，DFS搜索直到葉子節點，同時在stack中順序存儲已經訪問的節點。
2. 如果搜索到葉子節點，當前的葉子節點被設為最近鄰節點。
3. 然後通過stack回溯:
   如果當前點的距離比最近鄰點距離近，更新最近鄰節點.
   然後檢查以最近距離為半徑的圓是否和父節點的超平面相交.
   如果相交，則必須到父節點的另外一側，用同樣的DFS搜索法，開始檢查最近鄰節點。
   如果不相交，則繼續往上回溯，而父節點的另一側子節點都被淘汰，不再考慮的範圍中.
4. 當搜索回到root節點時，搜索完成，得到最近鄰節點。

參考：

• https://encyclopedia.thefreedictionary.com/Kd-tree
• https://baike.baidu.com/item/kd-tree/2302515