二分搜索樹是一種設計良好的有序集合，在平衡的情況下，查找search，插入insertion，刪除deletion都具有O(logn)的計算時間。本文討論實現二分搜索樹的具體細節。

 

二分搜索樹的每個結點包含key域，以及至多兩個孩子結點，並且左孩子小於當前結點的值，右孩子大於當前結點值。為了方便操作，每個結點還需要維護父結點的信息。從上面的描述可以看出，二分搜索樹的任何一個子樹同樣也是二分搜索樹。

 

搜索操作是所有操作的基礎。搜索操作可以很容易用遞歸過程描述：key>cur.key，則搜索右子樹；key<cur.key，則搜索左子樹；key==cur.key或者遇到空節點，則退出。

1 bool ST_BST::search(int val, ST_BST_Node* cur_node)
 2 {
 3     bool isFind=false;
 4     if(cur_node==nullptr)
 5     {
 6         printf("Search failed for node with value %d\n", val);
 7         return isFind;
 8     }
 9 
10     if(cur_node->value==val)
11     {
12         isFind=true;
13     }
14     else if(val < cur_node->value)
15     {
16         isFind=search(val, cur_node->left);
17     }
18     else
19     {
20         isFind=search(val, cur_node->right);
21     }
22 
23     return isFind;
24 }

插入操作找到需要插入的位置，然後創建結點，並加入該樹。

void ST_BST::insert(int val,ST_BST_Node* cur_node)
{
    if(val < cur_node->value)
    {
        if(cur_node->left==nullptr)
        {
            cur_node->left=createNode(val,cur_node);
        }
        else
        {
            insert(val, cur_node->left);
        }
    }
    else if(val > cur_node->value)
    {
        if(cur_node->right==nullptr)
        {
            cur_node->right=createNode(val,cur_node);
        }
        else
        {
            insert(val, cur_node->right);
        }
    }
}

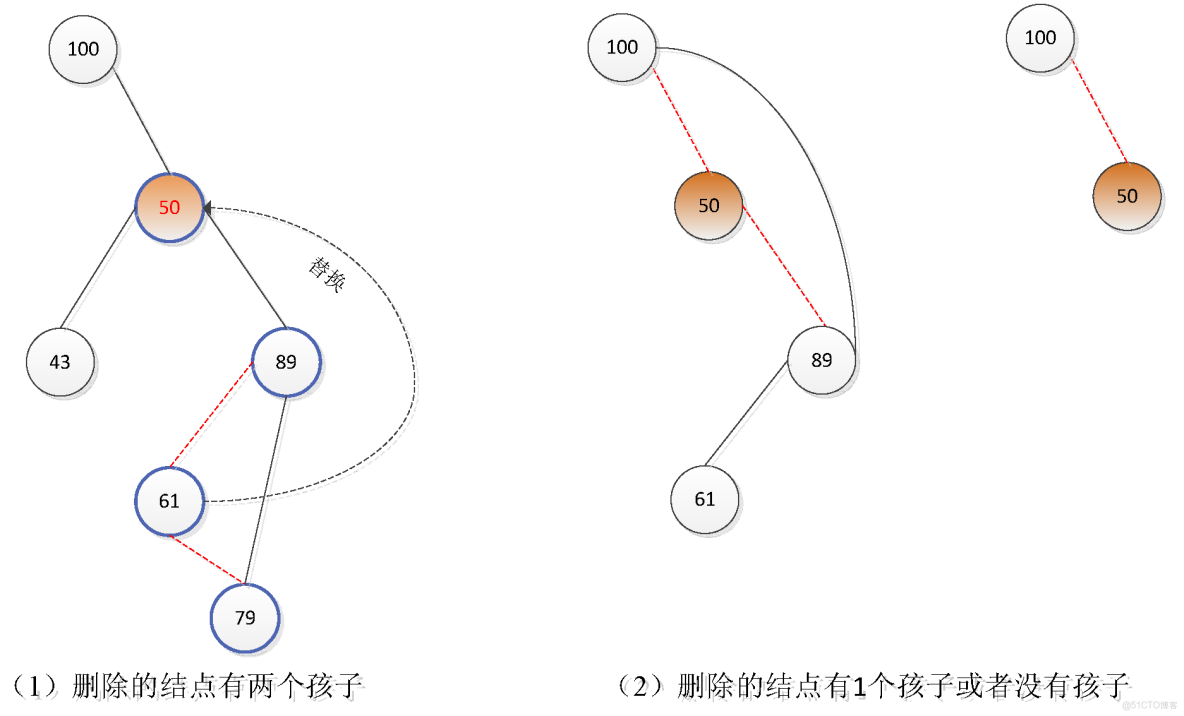
刪除操作相對於前面兩個操作稍顯複雜。


（1）假如刪除的結點有兩個孩子，則需要搜索該結點的後繼結點successor或者前驅結點predecessor來替換到該結點，然後再刪除successor或者predecessor. 其中successor是待刪除結點右子樹中最小的結點，而predecessor則是左子樹中最大的結點。

（2）

 

Treeselect提示中文Treeselect_搜索