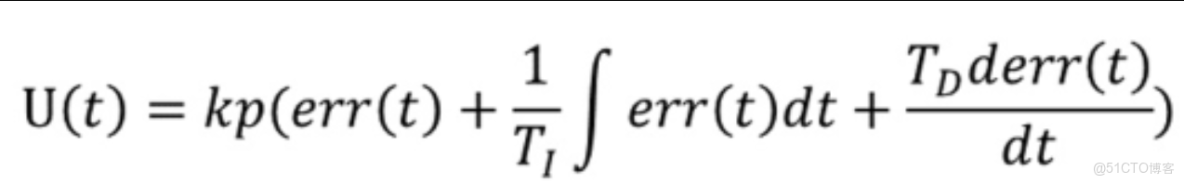讀完本篇文章你的收穫:
- PID三個參數基本概念
- 瞭解如何調節PID
- 認識一個鑽研技術的博主
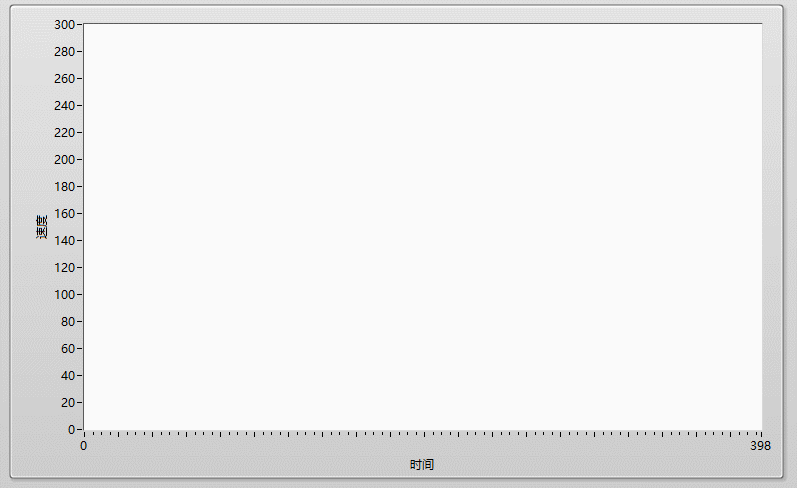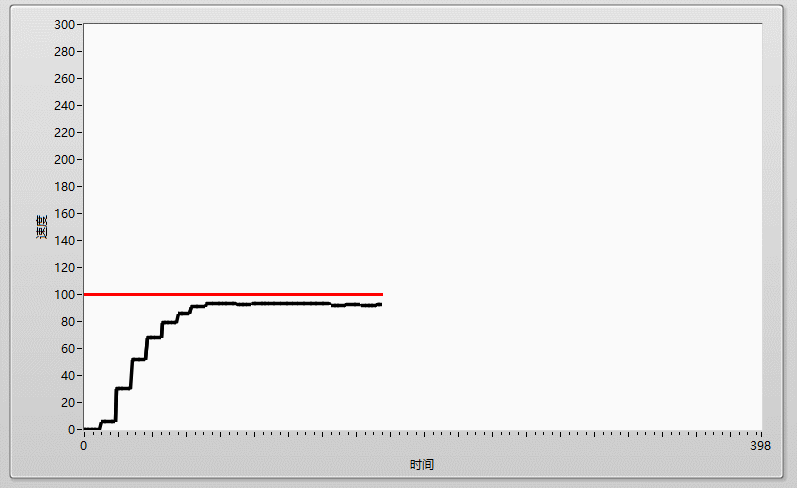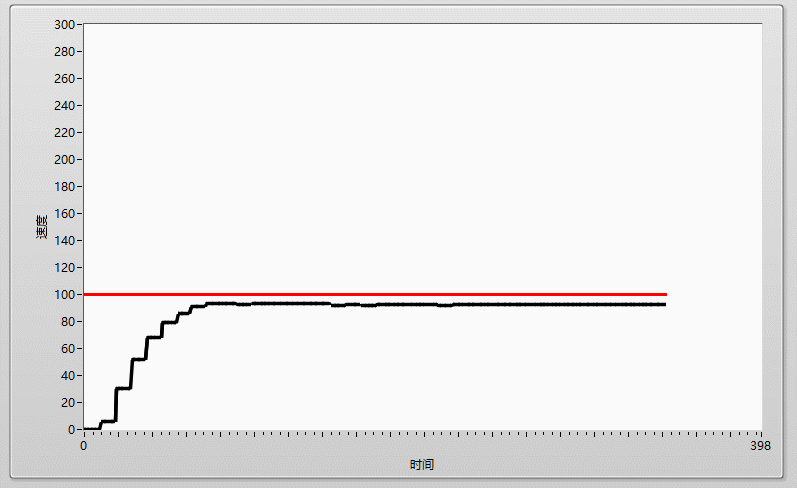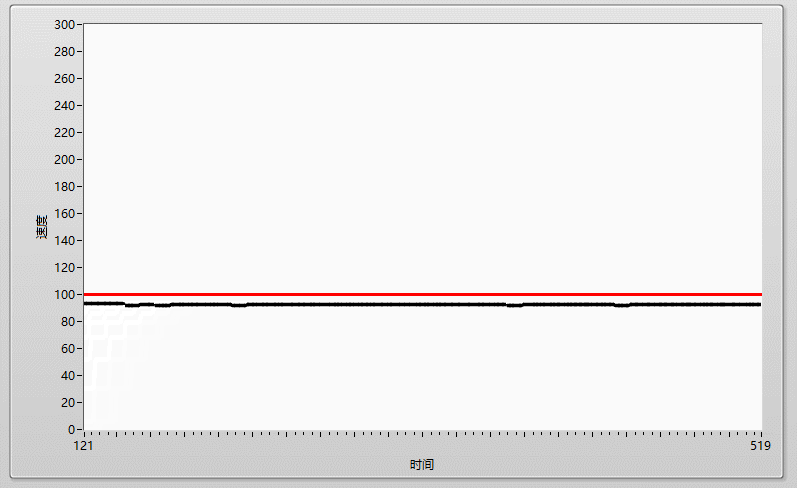
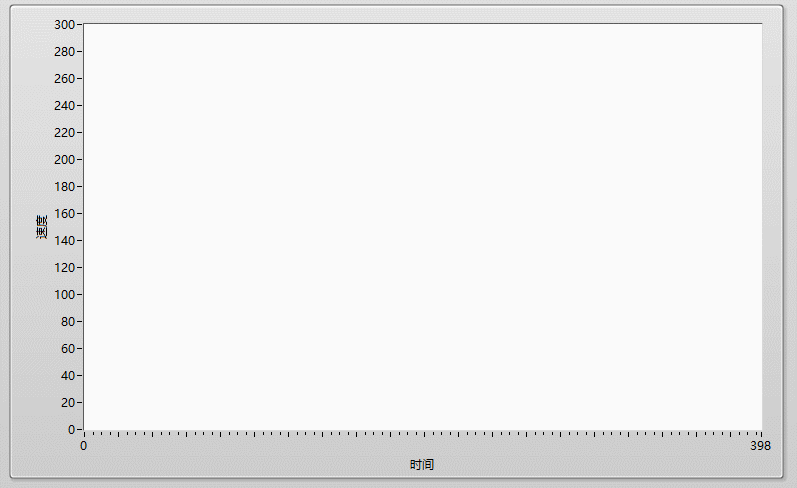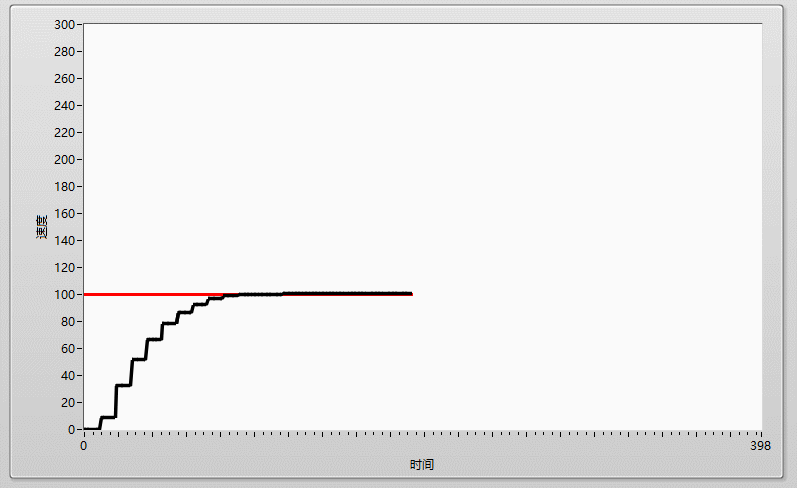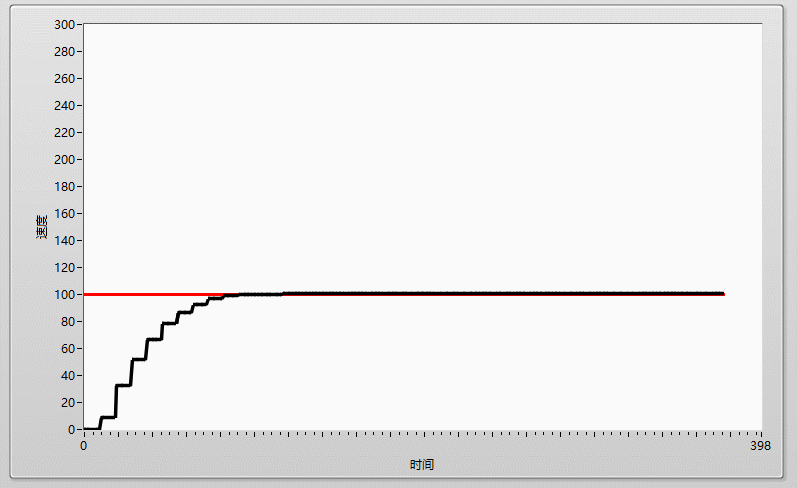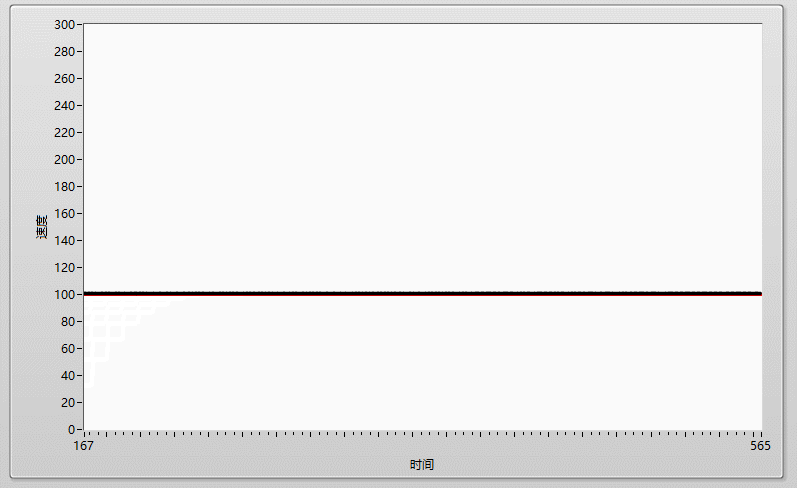
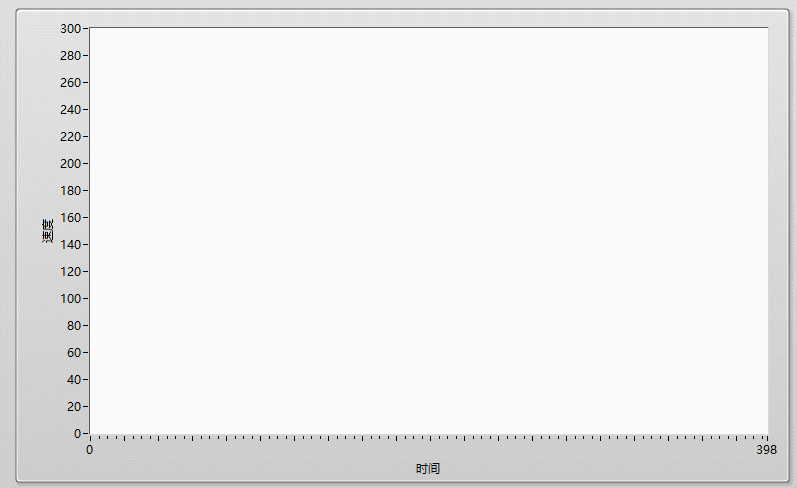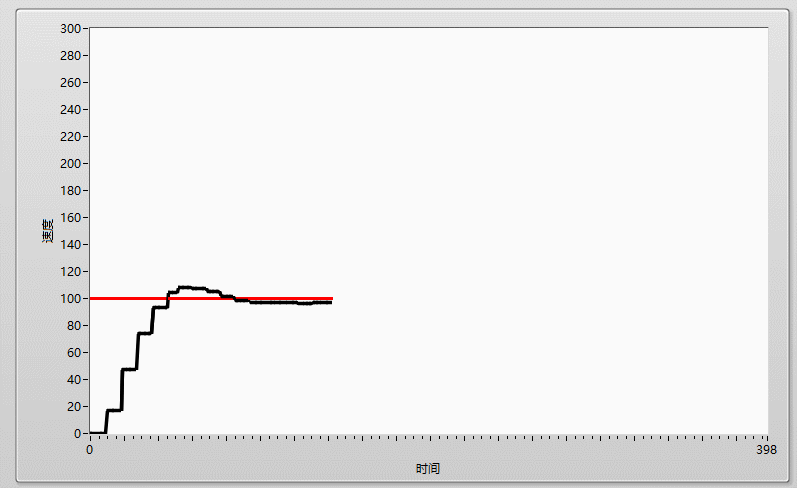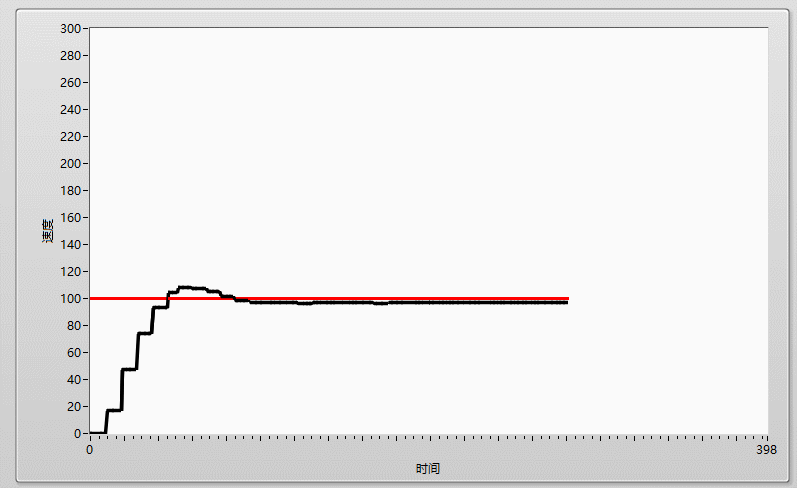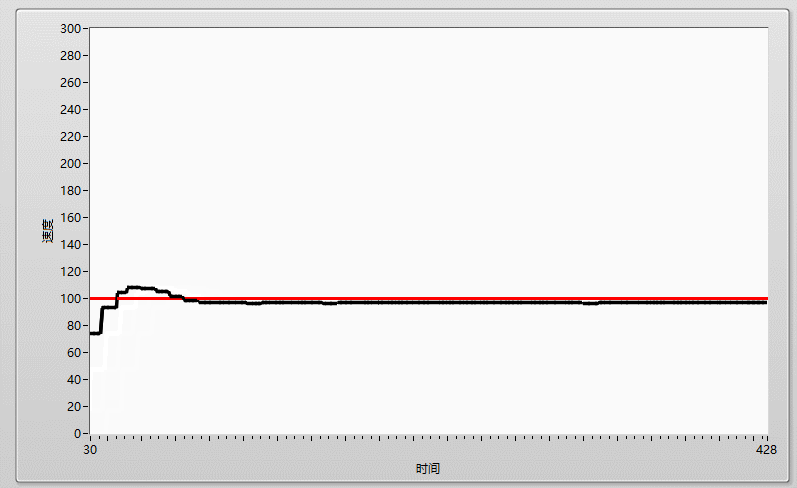
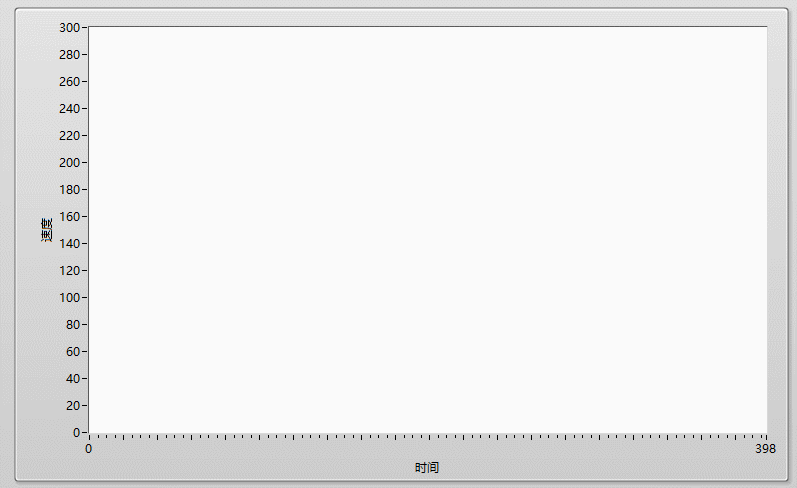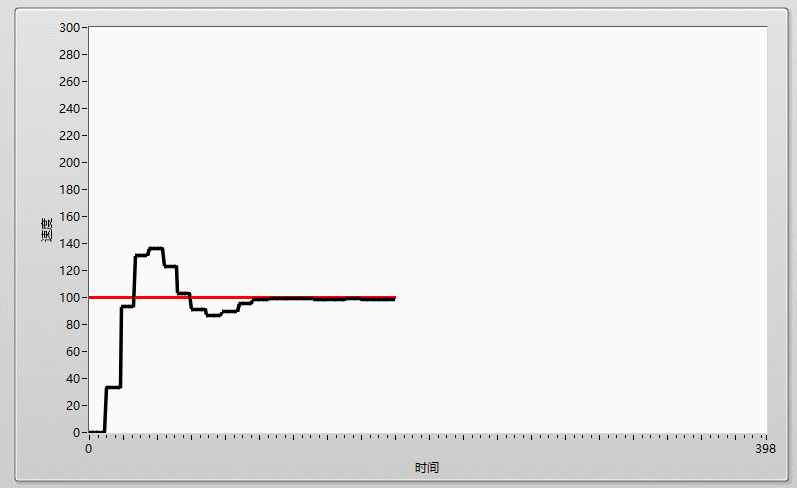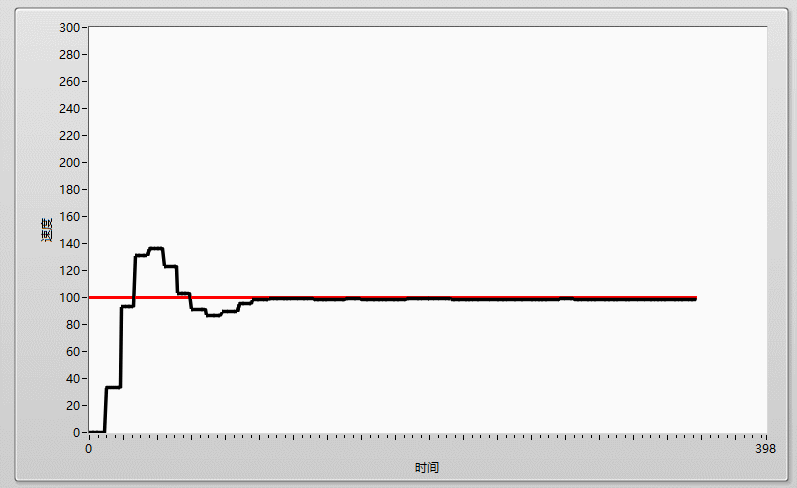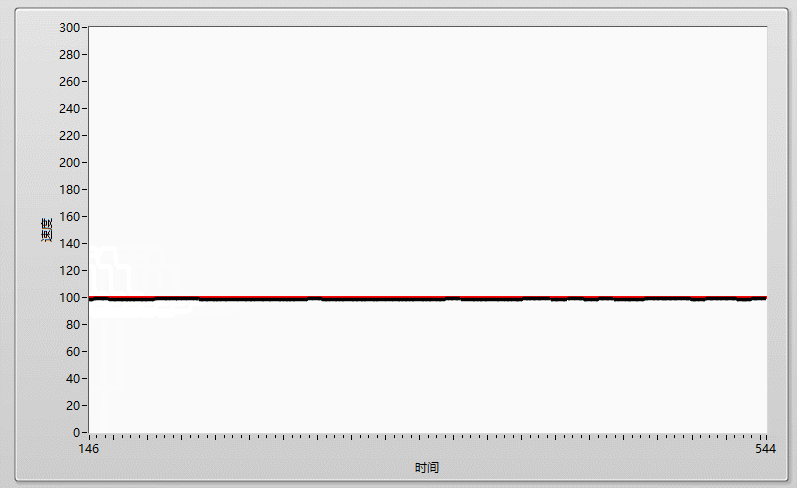
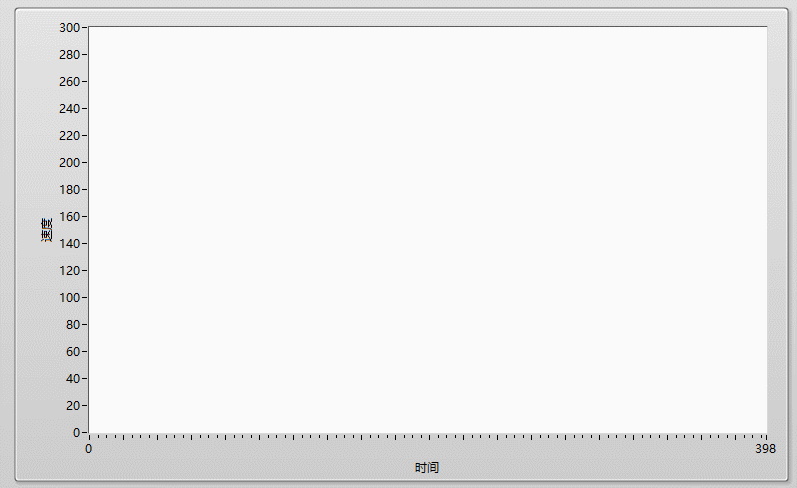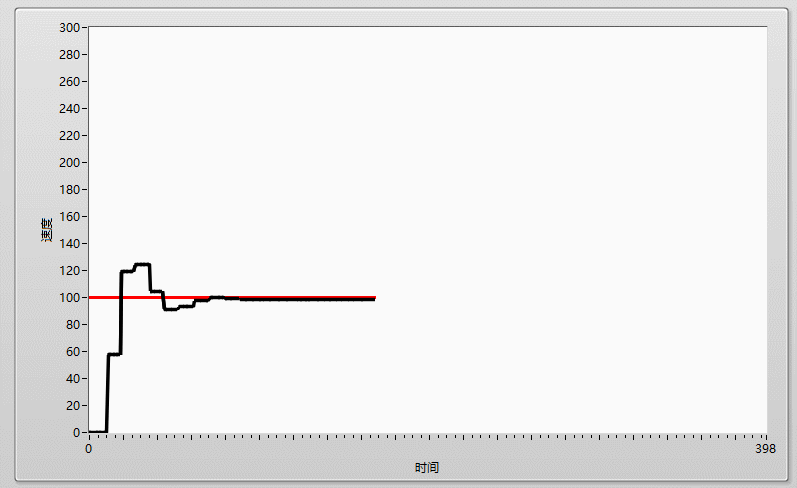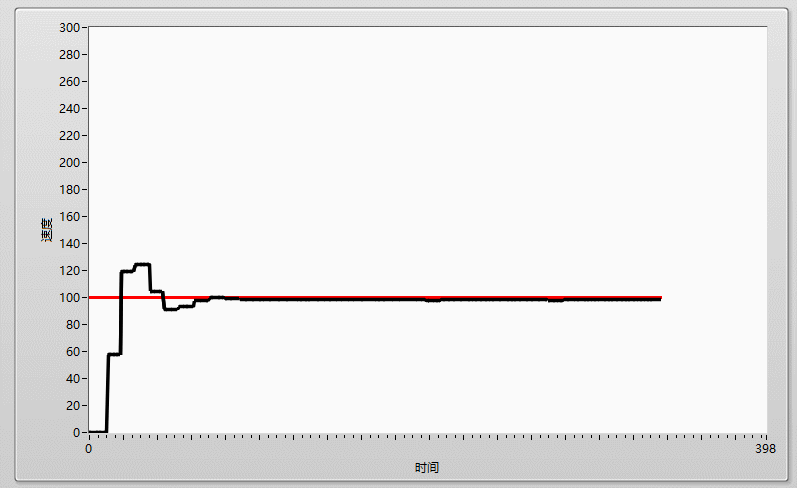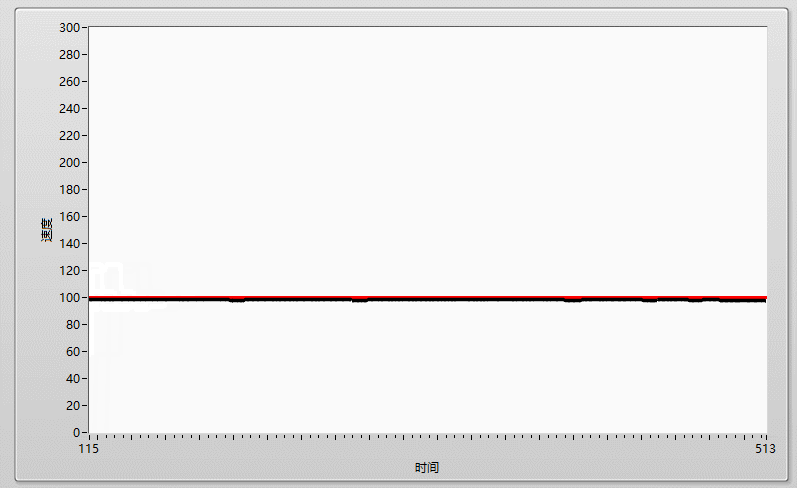
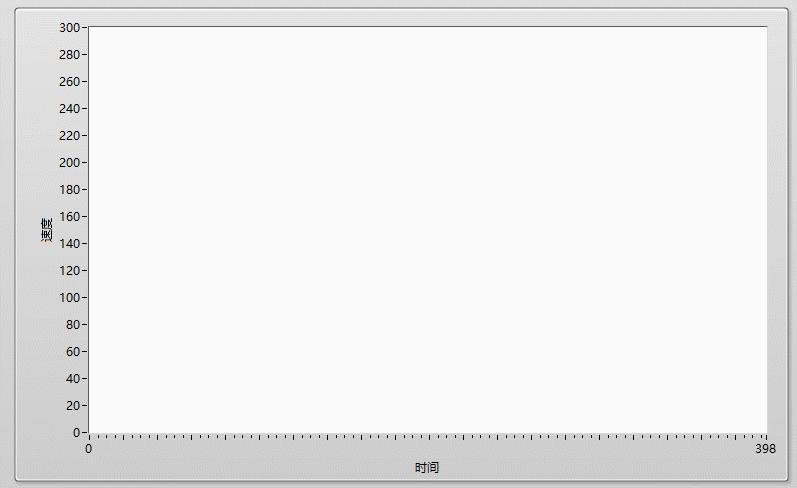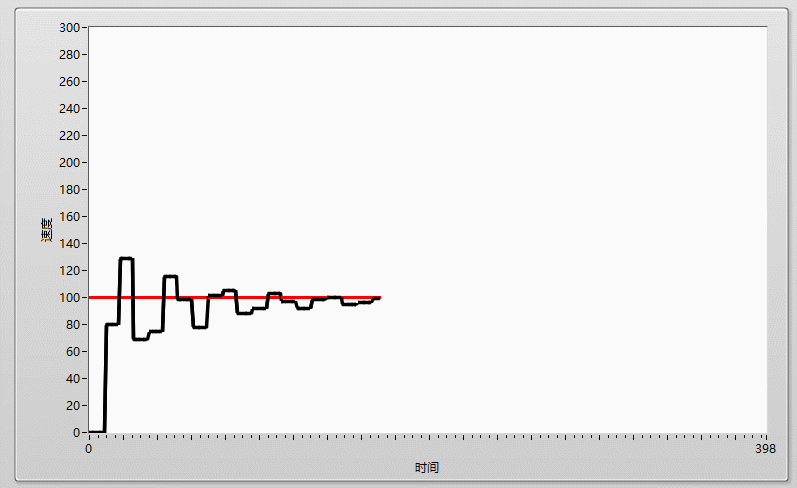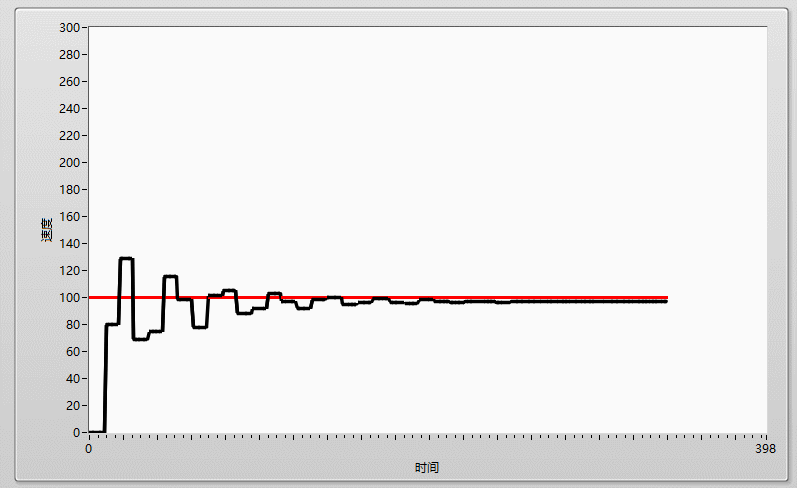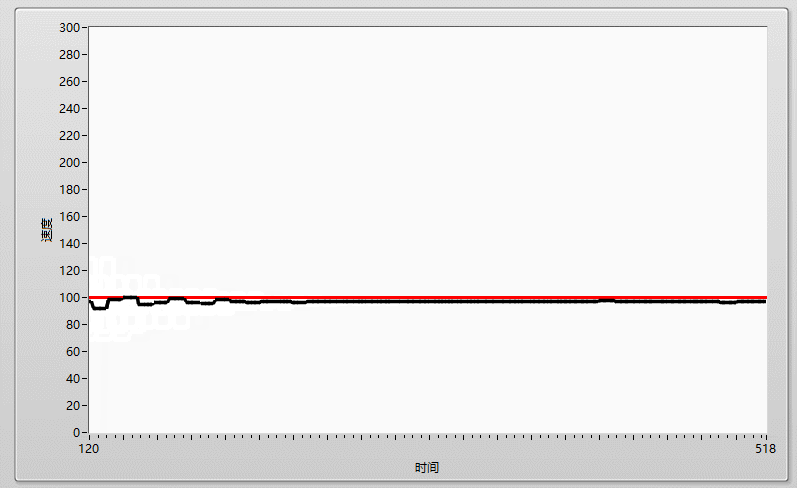
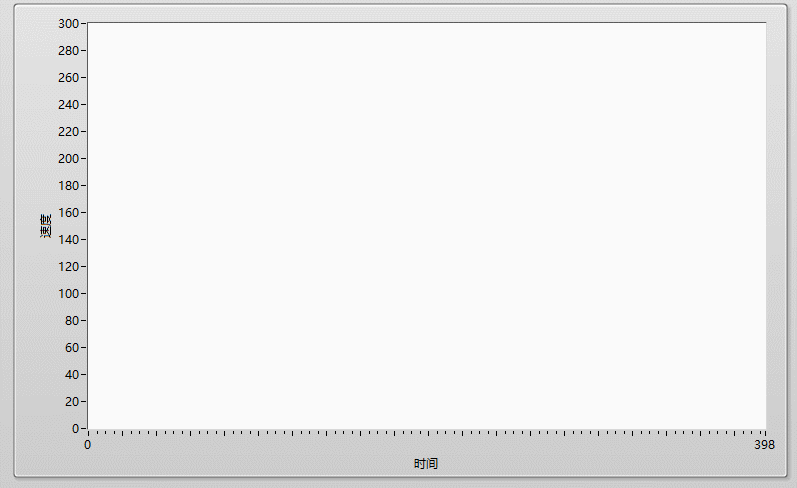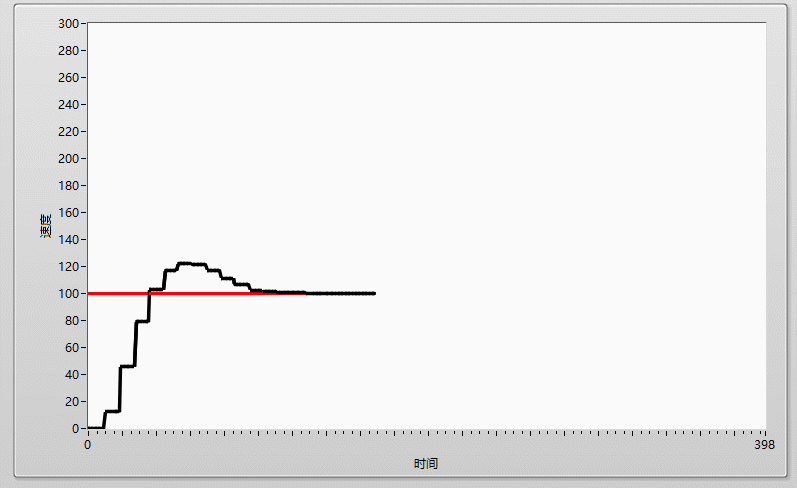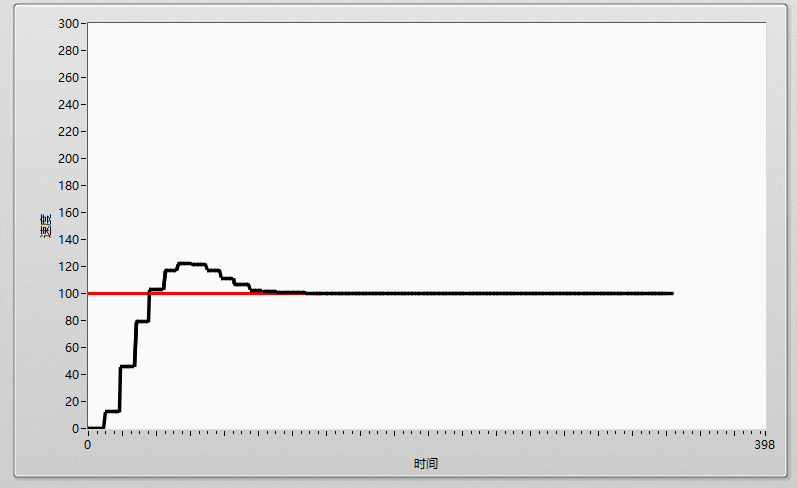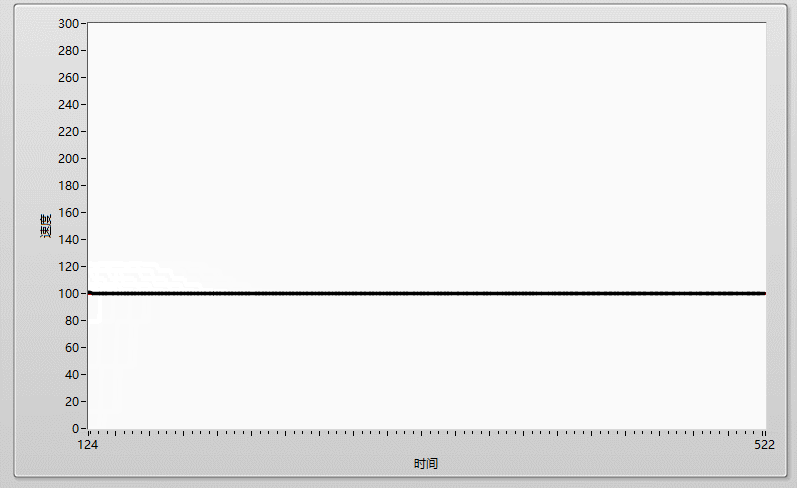
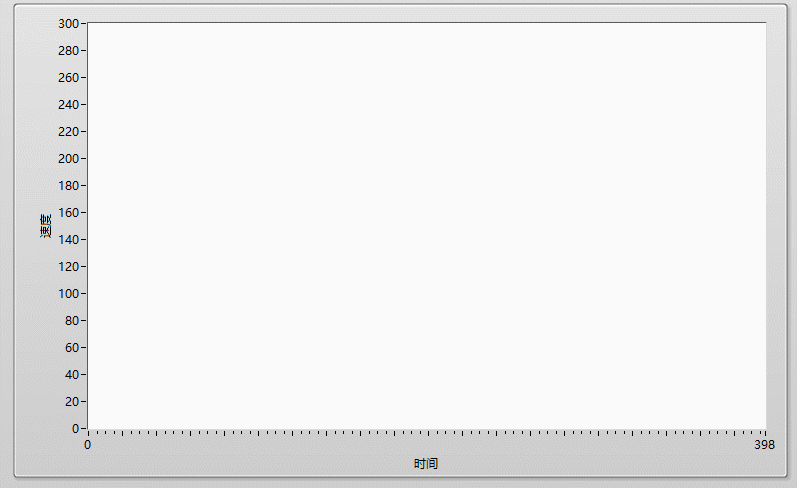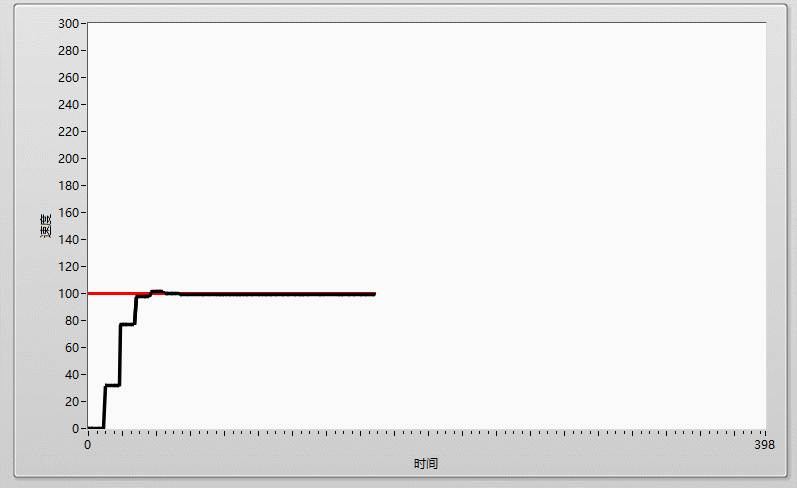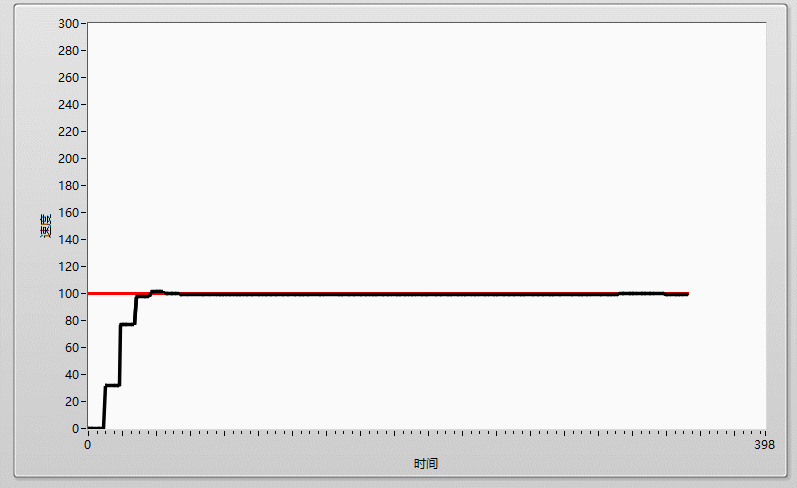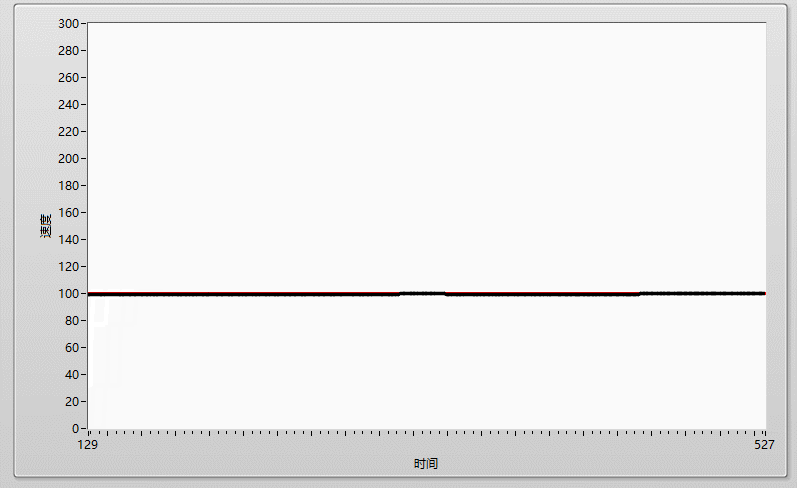
先上效果圖:
一、什麼是PID
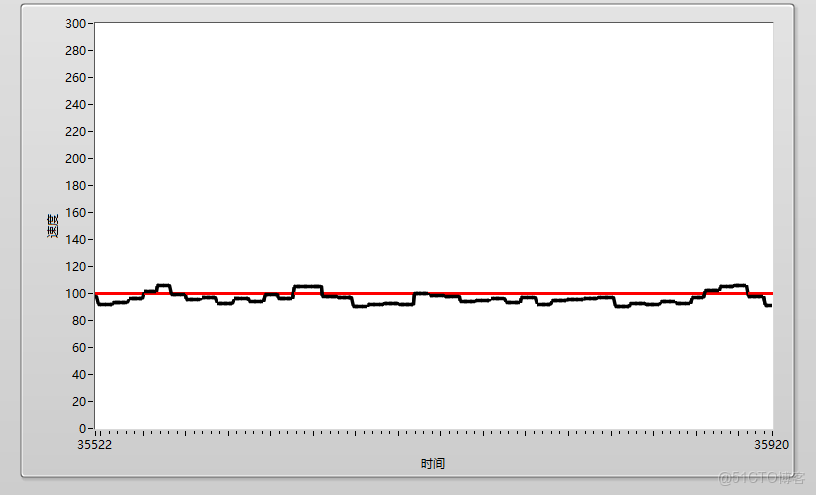
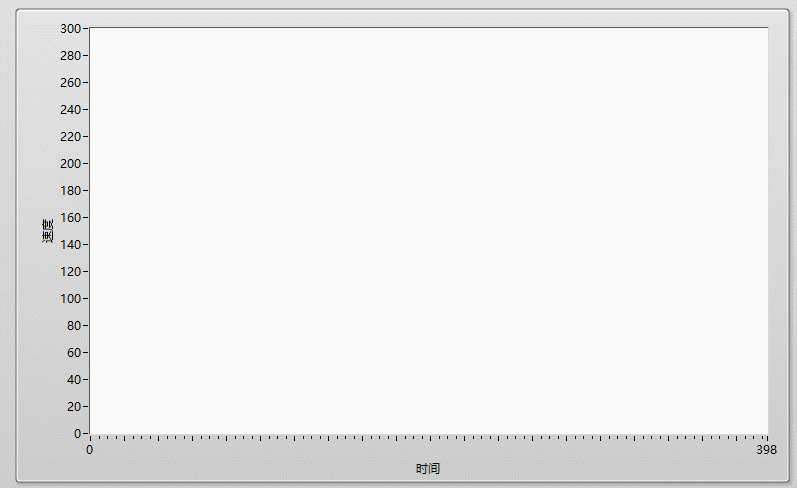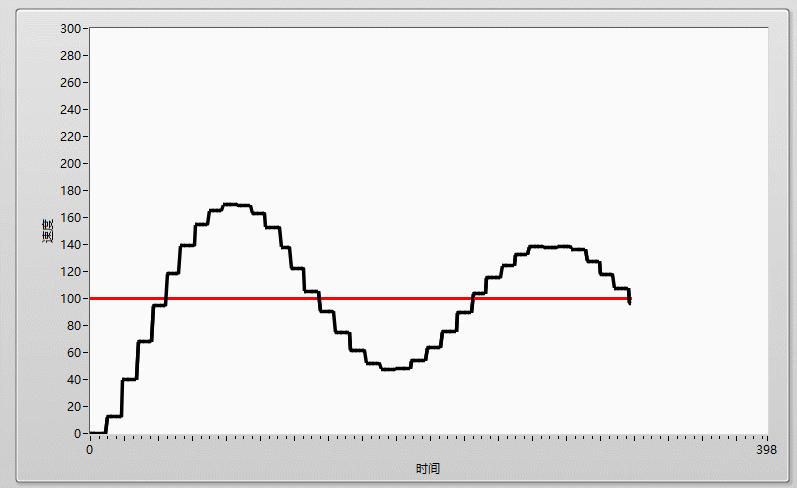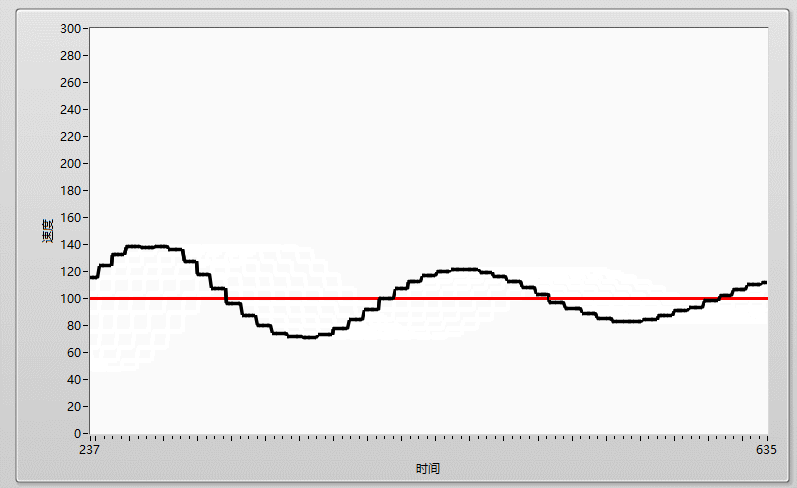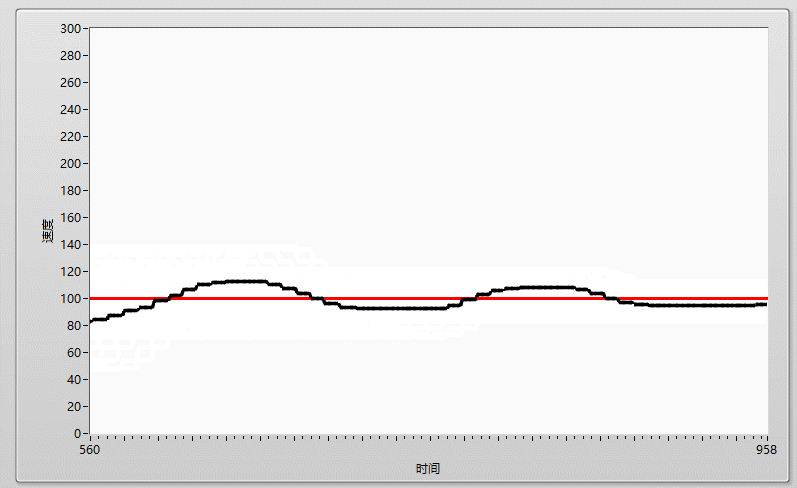
在工程中,如果我們要用單片機做一個温控系統,其系統組成一般如下:一個採集温度的ADC,一個輸出温度的加熱頭以及一個用於運行控制算法的單片機,如果我們要維持温度為100度,在不加任何控制算法的情況下,我們可以通過簡單的閾值判斷法來控制温度,一個if判斷語句,當採集到的温度大於100時,單片機控制加熱頭關閉,當採集的温度小於100度時,單片機則控制加熱頭開啓,簡單粗暴,但這樣的控制方法,最終所展示出來的温度曲線是極其不穩定的,他會由於控制器件的靈敏程度、加熱頭的性能等等原因,導致最終的温度曲線會在目標周圍震盪,達不到理想的控制效果,就像下圖:實際曲線(黑線) 在 目標曲線(紅線) 周圍抖動
那如何才能維持實際曲線與目標曲線貼合,達到一個穩定的控制效果呢?
這裏就引入了PID控制算法的概念,PID是 Proportion Integration Differentiation 的縮寫,實際上他就是一個公式,由比例項(Proportion ),積分項(Integration ),微分項(Differentiation) 三個部分組成,具體形式就是下面的公式:
其中err(t)就是當前值和目標值的誤差,PID的公式就是對這個誤差分別進行比例、積分、微分處理後疊加輸出,因為比例計算、積分計算、微分計算在數學公式上的計算定義不同,所以對應的項的輸出特性和輸入特性也有着不同,具體解釋如下:
1. 比例係數
比例控制係數,實際上就是先簡單的定義輸入與輸出的線性關係,假如我們輸出控制量的值得範圍在 100-1000,輸入的err誤差範圍卻在0.001-0.1;當誤差為0.1的時候輸出量需要到達到1000,這時我們就需要通過比例係數來構建輸入與輸出的線性關係
2. 積分系數
上一點我們分析了比例係數的含義,有小夥伴可能會好奇,比例係數加上後的效果其實和閾值判斷原理沒什麼區別,確實是這樣,只用上比例係數的效果和閾值判斷沒什麼區別,但別忘了,PID後面還有I和D兩項,其中I項的理解我們可以從積分的含義來理解,積分可以理解為在座標平面上,由曲線、直線以及軸圍成的曲形的面積值,這個曲線就是err(t)的函數,這個積分面積值就是代表過去一段時間的誤差累計值,我們把這個累計值乘以係數進行變換後,疊加到輸出上,就可以一定程度上消除歷史誤差對當前實際曲線的影響,提高系統的穩定性
3. 微分系數
微分的數學理解可以理解為當前誤差曲線的斜率,他可以用來預測當前曲線的未來走勢,對微分項的值進行處理後疊加,就可以預測當前值的未來趨勢,提高系統對未來變化反應能力
二、PID調節方式
通過上一小節的分析,我們對PID的三個項有了一個簡單的理解,但文字上的描述還是太抽象了,我以一個小車調速系統來做進一步講解,結合實際現象來分析PID三個參數的實際作用,以及如何調這三個參數,用到的實驗平台如下
- 平衡小車之家的主控板及電機
- 自己編寫的調試上位機
控制系統圖片:
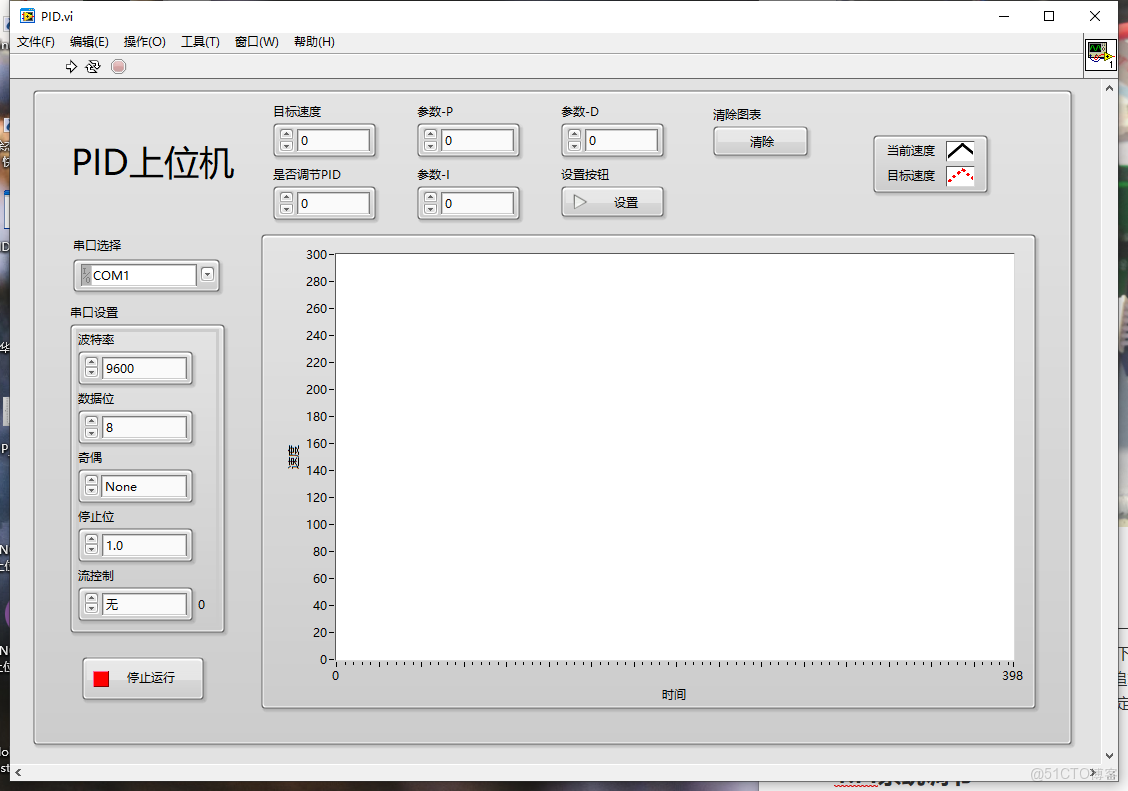
上位機界面:
我們在使用PID的時候,單獨只使用一個參數是沒有意義的至少使用兩個參數,並且P(比例項)是必須要有的,雖然PID有三個參數,但大多數情況下PID三個參數並不是都使用上的,一般會其中兩個來組合使用,比如PI組合用於追求穩定的系統,PD組合用於追求快速響應的系統,當然PID用於即追求穩定又追求快速響應的系統,但是實際上PID參數越多越難調,而且許多情況下兩個參數的效果已經足夠了,所以我一般根據情況使用前兩個,下面對這幾個系統都做一個分析
1.PI系統調節
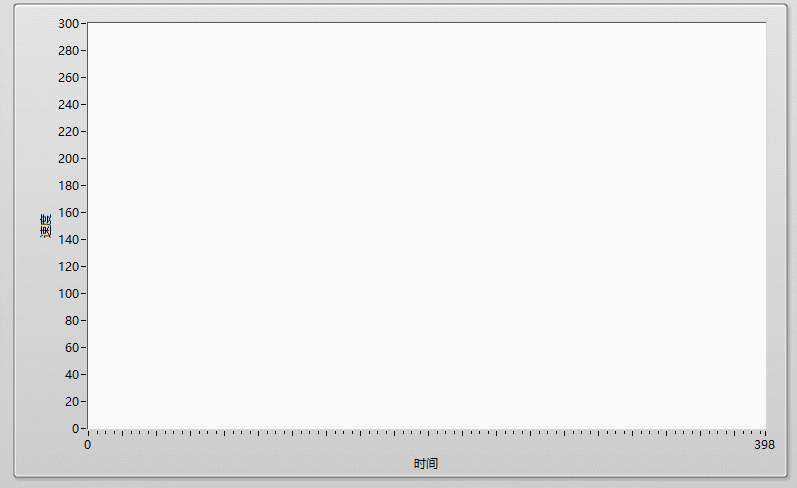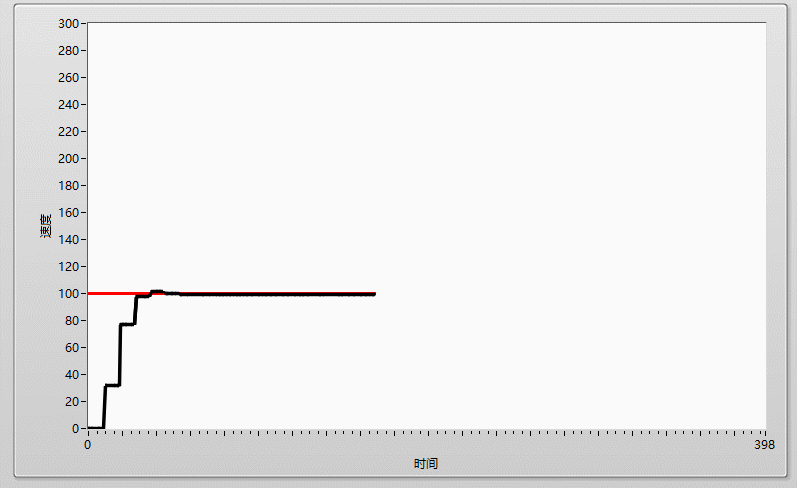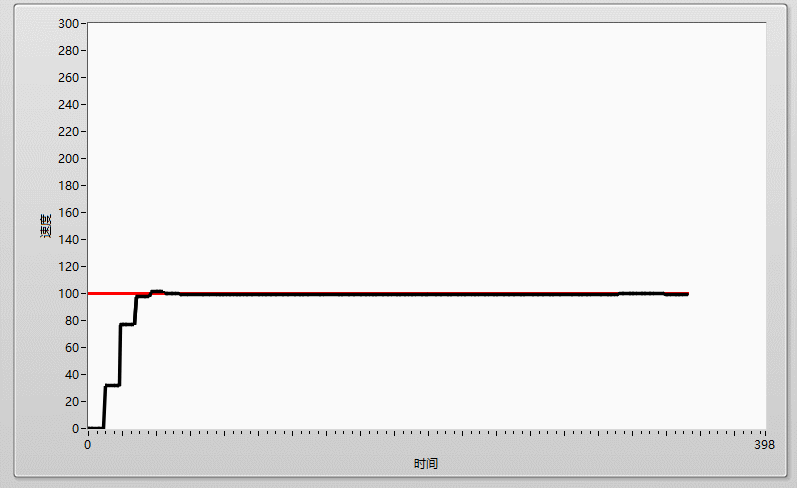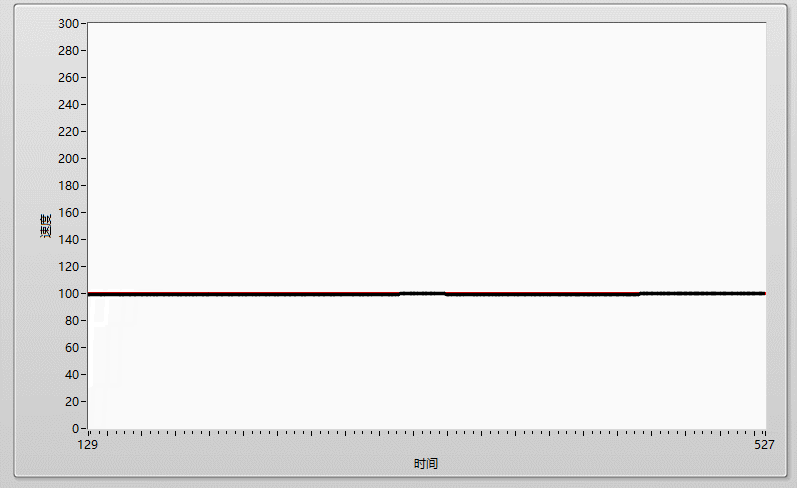
調節PI系統的第一步就是先調節P,由小到大依次調節,P的值可以很明顯的在輸出曲線體現出來,比如我先給P=0.05,系統反應如下,當P過小時,曲線呈現緩慢上升,且最終值會明顯低於目標值
當我們加大P到0.15時,我們可以看到實際曲線很快的接近目標值,但因為只有單純P控制,所以有較大的過沖(過沖就是實際值達到目標值時剎不住車,衝出去了),但在他穩定的時候,實際曲線基本接近目標曲線
如果P再增大到0.25,可以看到,實際曲線需要震盪很久才會達到穩定目標線,但在穩定後基本和目標線保持一致
如果P過大,整個系統就會不受控,實際曲線不會收斂到目標曲線位置,出現等幅震盪,比如P=0.45時
在調節PI系統時,P的選取一般有兩種情況
- P偏小一點,穩定時,實際值在目標值之下,一直存在誤差,這時再從0開始,一直加大I,消除穩定時的誤差,這種情況下的最終穩定曲線會一直保持在目標曲線之下,達到比較穩定的調節效果,不會有過沖(無過沖,穩定!)
- P大一點,在第一次到達目標值的時候有一定的過沖,但之後就會穩定,其與第一種相比反應速度更快!(有過沖,但他快!)
下面展示第一種PI控制方式,選取P=0.5(偏小)時,再用I消除穩定時的穩態誤差,達到穩定的效果:
I積分的值這裏我展示了三個,分別為較小,剛好,和較大時的實際曲線,用來做對比!
P=0.5,I=0.00005,I選取較小,可以看到相對於單純的P=0.5,穩定誤差有一定消除,但消除程度不夠!
在加大I到0.0001,剛剛好的時候,實際曲線和目標曲線基本重合!!!
當I過大取0.002時,因為累計誤差佔比過大,就會出現抖動現象,難以收斂
上面就是第一種PI調節情況,雖然PI系統平衡過程很穩定,但到達目標位置的反應速度較慢,有的時候為了提高反饋速度,適當的提高P,允許有一定的過沖,比如我取P=0.07,對應的I取0.0001時,波形如下,該系統允許一定的過沖,但可以更快的到達目標點後再趨於穩定,這就是第二種PI系統的調節方式
以上基本就是PI系統的調節過程了,下面我講一下PD系統的調節過程
2.PD系統調節
由一開始的概念我們可以知道,與 I 的不同點在於,I是計算累計誤差,而D則是計算未來趨勢,因此PD系統的反應速度更快,相對於PI系統會更快的到達目標位置附近,其調節方式首先還是調節P,這裏我們根據PI中P的調節結果,調節P到比大的位置,出現一定的過沖,這裏取P=0.15,不加D的時候圖形如下:
從圖像可以看出:P=0.15在開始時過沖嚴重,所以加上一個D來減小過沖幅度,D的選取和I的選取一樣,從0慢慢增加,觀看效果確定合適的點,下面一張圖的D=1.5是我試出來比較合適的點,我們可以看到加上合適的D之後,實際曲線到達目標位置的時間更短,過沖幅度也降低了一些,但是這裏效果不是很明顯,主要原因是我這裏使用的是小車輪子來做的速度PID,而PD的應用場合主要是大慣性系統中,這裏的應用場景不適合,但也能看出一定效果
如果D調節的過大之後,反倒會放大系統趨勢的影響,使系統出現震盪,難以穩定,如下D=5
3.PID系統調節
在講了PI和PD系統的調節方式後,下面分享一下PID系統的調節方式,首先我們先按照PI系統進行調節,先調P在調I,讓系統有一定的過沖後達到穩定,如下圖:
在出現了上面的 PI 波形之後,下面就開始調節D,慢慢增加D,將過沖補償掉,直到系統穩定,最終效果如下圖,PID系統就基本調節完成了
這篇文章的PID講解內容就到這裏了,下一篇文章將會詳細分享我常使用的PID調用代碼,幫助大家PID進一步入門。