思路：當前房屋偷與不偷取決於前一個或前兩個房屋是否被偷。所以當前狀態和前面狀態會有一種依賴關係，這種依賴關係就是動規的遞推公式。
動規五部曲：
1.確定dp數組（dp table）及其下標的含義：dp[i]表示考慮下標i（包括i）以內的房屋，最多可以偷竊的金額為dp[i]。
2.確定遞推公式：決定dp[i]的因素就是第i個房間偷還是不偷。
（1）如果要偷第i個房間，那麼dp[i] = dp[i - 2] + nums[i]。即第i - 1個房間一定是不考慮的，找出下標為i - 2（包括i - 2）以內的房間，最多可以偷竊的金額為dp[i - 2]加上第i個房間偷到的錢。
（2）如果不偷第i個房間：那麼dp[i] = dp[i - 1]，即考慮第i - 1個房間（注意這裏是考慮，並不是一定要偷第i - 1個房間）。
（3）然後dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i],dp[i - 1])。
3.dp數組如何初始化：
（1）從遞推公式dp[i] = max(dp[i - 2] + nums[i],dp[i - 1])可以看出，遞推公式的基礎就是dp[0]和dp[1]。
（2）從dp[i]的定義上來講，dp[0]一定是nums[0]，dp[1]就是nums[0]和nums[1]的最大值，即dp[1] = max(nums[0],nums[1])。
4.確定遍歷順序：dp[i]是根據dp[i - 2]和dp[i - 1]推導出來的，所以一定是從前向後遍歷。
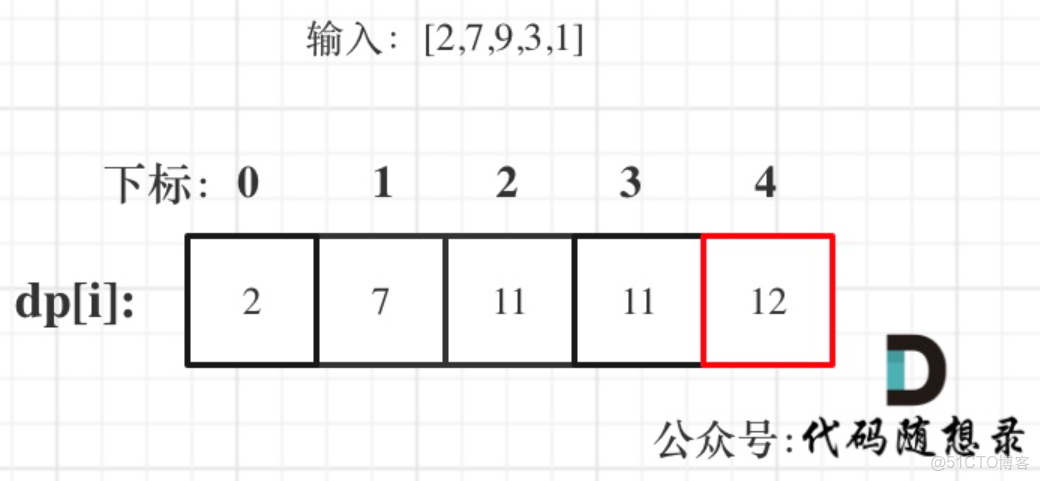
5.舉例推導dp數組：以[2,7,9,3,1]為例。
附代碼：
（一）一維dp
class Solution {
public int rob(int[] nums) {
if(nums == null || nums.length == 0){
return 0;
}
if(nums.length == 1){
return nums[0];
}
int[] dp = new int[nums.length];
dp[0] = nums[0];
dp[1] = Math.max(nums[0],nums[1]);
for(int i = 2;i < nums.length;i++){
dp[i] = Math.max(dp[i - 1],dp[i - 2] + nums[i]);
}
return dp[nums.length - 1];
}
}（二）滾動數組，將空間複雜度降低為3個空間
//使用滾動數組思想優化空間
//分析本題可以發現，所求結果僅依賴於前兩種狀態，此時可用滾動數組思想將空間複雜度降低為三個空間
class Solution {
public int rob(int[] nums) {
int len = nums.length;
if(len == 0){
return 0;
}
else if(len == 1){
return nums[0];
}
else if(len == 2){
return Math.max(nums[0],nums[1]);
}
//存放選擇的結果
int[] res = new int[3];
res[0] = nums[0];
res[1] = Math.max(nums[0],nums[1]);
for(int i = 2;i < len;i++){
res[2] = Math.max(res[0] + nums[i],res[1]);
res[0] = res[1];
res[1] = res[2];
}
return res[2];
}
}（三）進一步優化滾動數組，dp數組只存放與計算相關的兩次數據。
//進一步優化滾動數組空間，dp數組只存與計算相關的兩次數據
class Solution {
public int rob(int[] nums) {
if(nums.length == 1){
return nums[0];
}
//初始化dp數組
//優化空間，dp數組只用兩格空間，只記錄與當前計算相關的前兩個結果
int[] dp = new int[2];
dp[0] = nums[0];
dp[1] = Math.max(nums[0],nums[1]);
int res = 0;
for(int i = 2;i < nums.length;i++){
res = Math.max(dp[0] + nums[i],dp[1]);
dp[0] = dp[1];
dp[1] = res;
}
return dp[1];
}
}本文章為轉載內容，我們尊重原作者對文章享有的著作權。如有內容錯誤或侵權問題，歡迎原作者聯繫我們進行內容更正或刪除文章。
