從“2D轉3D”看圖形學的數學本質
在上一篇《從 0 構建 WAV 文件》中,我們拆解了音頻文件的底層:它不過是按規則排列的二進制採樣點。當時我們得出了一個結論:計算機的世界沒有魔法,只有樸素的規則。
當你玩《黑神話:悟空》或《賽博朋克 2077》時,你是否好奇過:屏幕明明是一個平面,為什麼我們能從中看出真實的3d效果? 那些複雜的 3D 遊戲,其底層邏輯是否也像 WAV 文件一樣,是由某個簡單的“規則”構建的?
答案是肯定的。3D 視覺的本質,其實就是一個簡單的數學除法。
核心法則:透視投影
計算機之所以能“欺騙”我們的眼睛,靠的是透視(Perspective)。
在現實中,光線沿直線傳播。遠處的物體在視網膜上成像小,近處的成像大,即“近大遠小”。計算機要實現 3D 效果,本質上就是要把空間中的 3D 座標 (x, y, z),通過某種規則變換成屏幕上的 2D 座標 (x', y')。
幾何建模:尋找相似三角形
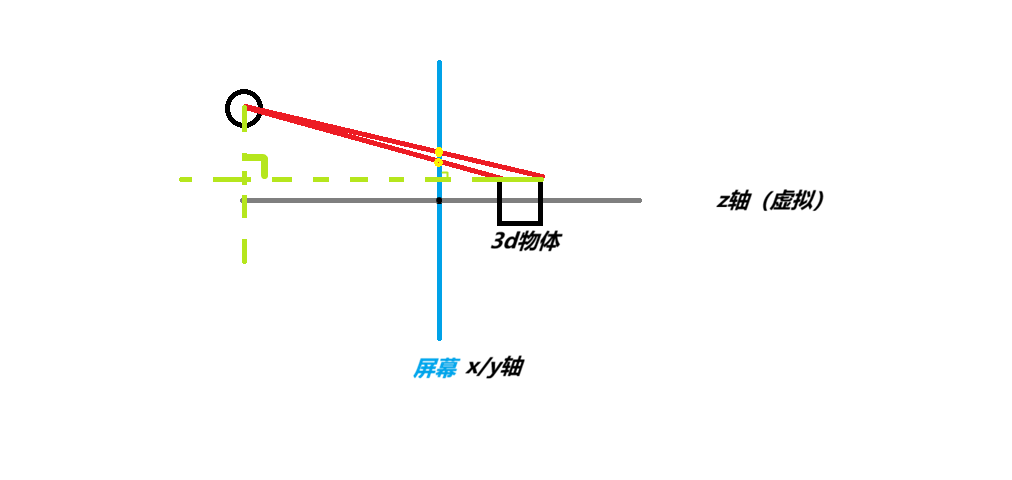
為了找到這個變換規則,我們可以構建一個極簡的幾何模型。想象你正坐在屏幕前:
- 觀察點:你的眼睛。
- 投影面:你面前的電腦屏幕(設中心為原點)。
- 3D 物體:屏幕後方空間裏的一個點,座標為 \((x, y, z)\),其中 \(z\) 是它距離你眼睛的深度。
當光線從物體出發射向你的眼睛時,必然會穿過屏幕。這個交點,就是該物體在屏幕上顯示的正確位置。
如果我們從側面觀察這個模型,以眼睛、屏幕交點、物體真實位置為頂點,可以構建出兩個相似三角形:
數學表達:神奇的 “除以 Z”
利用初中數學中“相似三角形對應邊成比例”的原理,設眼睛到屏幕的距離為 \(d\)(類似於相機的焦距),我們可以推導出屏幕座標 \(x'\) 與空間座標 \(x, z\) 的關係:
同理,對於 \(y\) 軸:
這就是 3D 圖形學的基本原理:3D 轉 2D 的本質就是“除以 Z”。
- 當物體走遠時,\(z\) 變大,除出來的結果 \(x', y'\) 就越小(向屏幕中心收縮)。
- 當物體靠近時,\(z\) 變小,除出來的結果變大(向屏幕邊緣擴張)。
這就是為什麼我們在走廊裏往前走,兩邊的牆壁會向四周“散開”的原因。
從數據到畫面:像構建 WAV 一樣構建 3D
我們可以通過幾個運用先前給出的公式完成3d圖形繪製的例子來證明該公式的正確性:
import turtle
# --- 1. 核心數學規則:透視投影 (來自博客公式) ---
def project(x, y, z):
"""
本質公式:x' = x / z, y' = y / z
我們乘上一個係數 400 (視距 d),是為了讓畫面大一點,方便觀察
"""
d = 400
x_2d = (x / z) * d
y_2d = (y / z) * d
return x_2d, y_2d
# --- 2. 定義 3D 數據 (8個頂點的 x, y, z) ---
# 我們讓前四個點的 z=2 (近),後四個點的 z=3 (遠)
vertices = [
# 前面的四個頂點 (z=2, 離眼睛近,看起來大)
[-1, -1, 2], [1, -1, 2], [1, 1, 2], [-1, 1, 2],
# 後面的四個頂點 (z=3, 離眼睛遠,看起來小)
[-1, -1, 3], [1, -1, 3], [1, 1, 3], [-1, 1, 3]
]
# 定義哪些點需要連成線 (索引號)
edges = [
(0,1), (1,2), (2,3), (3,0), # 連接前臉的4條邊
(4,5), (5,6), (6,7), (7,4), # 連接後臉的4條邊
(0,4), (1,5), (2,6), (3,7) # 連接前後臉的4條縱向邊
]
# --- 3. 執行投影計算 ---
# 將 3D 座標轉換成 2D 座標
points_2d = []
for v in vertices:
p_2d = project(v[0], v[1], v[2])
points_2d.append(p_2d)
# --- 4. 繪圖部分 ---
screen = turtle.Screen()
screen.title("2D轉3D本質演示:靜態立方體")
t = turtle.Turtle()
t.pensize(2)
t.speed(1) # 慢速繪圖,觀察過程
for edge in edges:
start_idx = edge[0]
end_idx = edge[1]
# 移動到起點
t.up()
t.goto(points_2d[start_idx])
# 畫線到終點
t.down()
t.goto(points_2d[end_idx])
t.hideturtle()
print("繪製完成!觀察近處的面(z=2)是否比遠處的面(z=3)大?")
turtle.done()
這個例子演示了一個靜態的立方體是如何繪製的,當然,有人會説只要打好點也能做到與程序類似的效果,那麼我們在用一個動態的旋轉立方體來證明公式的正確性:
import turtle
import math
import time
# --- 1. 核心數學規則:透視投影 ---
def project(x, y, z, fov, viewer_distance):
"""
將 3D 座標變換為 2D 座標
本質公式:x' = x / z, y' = y / z
"""
# 這裏的 z 需要加上 viewer_distance,防止物體就在眼睛上導致除以 0
factor = fov / (viewer_distance + z)
x_2d = x * factor
y_2d = y * factor
return x_2d, y_2d
# --- 2. 定義立方體的數據結構 ---
# 8個頂點 (x, y, z)
vertices = [
[-1, -1, 1], [1, -1, 1], [1, 1, 1], [-1, 1, 1],
[-1, -1, -1], [1, -1, -1], [1, 1, -1], [-1, 1, -1]
]
# 12條稜 (連接頂點的索引)
edges = [
(0,1), (1,2), (2,3), (3,0), # 前面
(4,5), (5,6), (6,7), (7,4), # 後面
(0,4), (1,5), (2,6), (3,7) # 連接前後的線
]
# --- 3. 設置畫布 ---
screen = turtle.Screen()
screen.bgcolor("black")
screen.setup(width=600, height=600)
screen.tracer(0) # 關閉自動刷新,手動控制動畫
t = turtle.Turtle()
t.ht() # 隱藏畫筆圖標
t.color("#00FF00") # 極客綠
t.pensize(2)
# --- 4. 動畫循環 ---
angle = 0
while True:
t.clear()
# 存儲投影后的 2D 點
projected_points = []
# 每一幀都旋轉一下座標,讓它動起來
angle += 0.02
for v in vertices:
# 旋轉矩陣(簡單的繞 Y 軸和 X 軸旋轉數學)
# 這一步是為了讓數據“動”起來,不是投影的本質
x, y, z = v
# 繞 Y 軸轉
nx = x * math.cos(angle) - z * math.sin(angle)
nz = x * math.sin(angle) + z * math.cos(angle)
# 繞 X 軸轉
ny = y * math.cos(angle*0.7) - nz * math.sin(angle*0.7)
nz = y * math.sin(angle*0.7) + nz * math.cos(angle*0.7)
# --- 調用本質公式 ---
# fov(視距)設為 400,viewer_distance(物體離眼睛距離)設為 4
p2d = project(nx, ny, nz, 400, 4)
projected_points.append(p2d)
# 繪製稜
for edge in edges:
p1 = projected_points[edge[0]]
p2 = projected_points[edge[1]]
t.up()
t.goto(p1)
t.down()
t.goto(p2)
screen.update() # 刷新屏幕
time.sleep(0.01)
turtle.done()
這個樣例中,同樣使用了剛才給出的公式,不過增加了一個新的公式,用於控制向量的旋轉,即線條的旋轉,以實現旋轉的效果:
腦補維度:當這些點被連成線、貼上材質、加上光影,人類的大腦就會自動根據“近大遠小”的視覺經驗,幫我們“腦補”出那消失的第三個維度。
重塑數字世界的信心
從 WAV 文件的二進制流,到 3D 遊戲的透視投影,我們能發現一個共同點:複雜的表象下,底層邏輯往往較為簡單。
- 聲音:是按採樣率排列的數值。
- 空間:是座標點除以深度的變換。
當我們不再把 3D 技術看作某種不可逾越的“黑盒”,而是看作一系列幾何規則的組合時,你便擁有了重塑數字世界的能力。正如我們能手動拼出一個 WAV 文件一樣,只要掌握了座標變換的邏輯,你也能在代碼的荒原上,徒手構建出一個屬於你的三維宇宙。