2025-11-14：移除相鄰字符後字典序最小的字符串。用go語言，給出一個只包含小寫字母的字符串 s。你可以多次（也可以不做任何操作）執行如下步驟：任意選取一對相鄰字符，如果這兩個字母在字母表中相鄰詳情 - 字符串,include,初始化,Go語言,後端開發福大大架構師每日一題動態日志

動態

詳情

2025-11-14：移除相鄰字符後字典序最小的字符串。用go語言，給出一個只包含小寫字母的字符串 s。你可以多次（也可以不做任何操作）執行如下步驟：任意選取一對相鄰字符，如果這兩個字母在字母表中相鄰

05:23 下午 · 11月 15 ,2025

2025-11-14：移除相鄰字符後字典序最小的字符串。用go語言，給出一個只包含小寫字母的字符串 s。你可以多次（也可以不做任何操作）執行如下步驟：任意選取一對相鄰字符，如果這兩個字母在字母表中相鄰——順序不限（例如 'a' 與 'b' 或 'b' 與 'a'），且字母表循環連接（'a' 與 'z' 也視為相鄰）——就同時刪除這兩個字符，剩下的字符自動向左收縮合並。經過任意次這樣的刪除後，目標是讓最終得到的字符串在字典序上儘可能小。字典序按常規定義比較：從左到右找第一個不同字符，字母表靠前者更小；若一個字符串是另一個的前綴，則更短的那個更小。輸出能達到的最小字典序字符串。

1 <= s.length <= 250。

s 僅由小寫英文字母組成。

輸入： s = "zdce"。

輸出： "zdce"。

解釋：

從字符串中移除 "dc"，剩下 "ze"。

無法對 "ze" 進行更多操作。

然而，由於 "zdce" 的字典序小於 "ze"。因此，經過所有可能的移除後，字典序最小的字符串是 "zdce"。

題目來自力扣3563。

算法步驟詳細描述

初始化與預處理
- 算法首先計算字符串 s 的長度 n。
- 創建一個大小為 n x n 的二維布爾數組 canBeEmpty。這個數組用於記錄子串 s[i:j+1]（即從索引 i 到索引 j 的子串）是否可以通過題目描述的移除操作被完全刪除（即變為空字符串）。canBeEmpty[i][j] = true 表示該子串可被完全移除。
動態規劃填充 canBeEmpty 表
- 填充順序是從字符串的末尾開始，向前處理較小的子串，逐步擴展到整個字符串。具體來説，索引 i 從 n-2 遞減到 0，對於每個 i，索引 j 從 i+1 開始，以步長2遞增到 n-1（因為每次移除兩個字符，只有長度為偶數的子串才有可能被完全移除）。
- 對於每一對 (i, j)，通過以下兩種方式判斷子串 s[i:j+1] 是否可被完全移除：
  - 直接移除兩端字符：如果子串兩端的字符 s[i] 和 s[j] 在字母表上是相鄰的（包括循環相鄰，如 'a' 和 'z'），並且它們之間的子串 s[i+1:j] 已經被判定為可完全移除（即 canBeEmpty[i+1][j-1] 為 true），那麼移除中間部分後再移除這對相鄰字符，整個子串就可以被清空。此時，將 canBeEmpty[i][j] 設為 true。
  - 分割為兩個可移除子串：如果存在一個分割點 k（i+1 到 j-2 之間，且步長為2），使得子串 s[i:k+1] 和 s[k+1:j+1] 都可以被完全移除（即 canBeEmpty[i][k] 和 canBeEmpty[k+1][j] 均為 true），那麼整個子串 s[i:j+1] 也可以被移除。算法會檢查所有可能的分割點 k，一旦找到滿足條件的分割點，就將 canBeEmpty[i][j] 設為 true。
構造最小字典序結果字符串
- 創建一個字符串數組 f，其長度為 n+1。f[i] 表示從原始字符串的第 i 個位置開始（即子串 s[i:]）到末尾，經過若干次移除操作後能得到的字典序最小的字符串。
- 從字符串末尾開始向前計算（i 從 n-1 遞減到 0）：
  - 基礎情況：f[n] 被初始化為空字符串，表示超出字符串末尾的情況。
  - 對於每個位置 i，考慮兩種可能，並選擇字典序更小的結果作為 f[i]：
    - 保留當前字符 s[i]：將 s[i] 與後面子串的結果 f[i+1] 拼接起來，形成一種可能的結果。
    - 移除從 i 開始的某個子串：遍歷所有可能的 j（j 從 i+1 到 n-1，步長為2），如果子串 s[i:j+1] 可以被完全移除（即 canBeEmpty[i][j] 為 true），那麼可以考慮直接跳過這個子串，將後面子串的結果 f[j+1] 作為當前的可能結果。這是因為移除這個子串不會在結果中留下任何字符。
  - 在所有上述可能的結果中，使用字典序比較（從左到右第一個不同字符決定大小，前綴更短的更小），選擇最小的那個字符串賦值給 f[i]。
返回最終結果
- 整個過程的最終結果是 f[0]，它代表了從字符串開頭到末尾的整個字符串經過操作後能得到的最小字典序字符串。

複雜度分析

總的時間複雜度：**O(n³)**。
- 填充 canBeEmpty 表需要三層循環：外層循環 i 為 O(n)，內層循環 j 為 O(n)，最內層尋找分割點 k 的循環也是 O(n)。因此這部分是 O(n³)。
- 構造結果字符串 f 的過程也需要兩層循環：外層循環 i 為 O(n)，內層循環 j 為 O(n)。但在每次比較和拼接字符串時，最壞情況下字符串長度可能為 O(n)，因此這部分的時間複雜度也是 O(n³)。
- 綜上，算法的總時間複雜度為 O(n³)。
總的額外空間複雜度：**O(n²)**。
- 主要用於存儲二維數組 canBeEmpty，它佔用 O(n²) 的空間。
- 字符串數組 f 存儲了 n+1 個字符串，在最壞情況下，每個字符串的長度可能為 O(n)，因此存儲 f 也需要 O(n²) 的空間。
- 因此，算法的總空間複雜度為 O(n²)。

這個算法通過動態規劃系統地探索了所有移除可能性，並確保最終得到的是字典序最小的結果。對於題目中約定的字符串長度（n <= 250），O(n³) 的複雜度在可接受範圍內。

Go完整代碼如下：

package main

import (
	"fmt"
)

func isConsecutive(x, y byte) bool {
	d := abs(int(x) - int(y))
	return d == 1 || d == 25
}

func lexicographicallySmallestString(s string) (ans string) {
	n := len(s)
	canBeEmpty := make([][]bool, n)
	for i := range canBeEmpty {
		canBeEmpty[i] = make([]bool, n)
	}
	for i := n - 2; i >= 0; i-- {
		canBeEmpty[i+1][i] = true // 空串
		for j := i + 1; j < n; j += 2 {
			// 性質 2
			if isConsecutive(s[i], s[j]) && canBeEmpty[i+1][j-1] {
				canBeEmpty[i][j] = true
				continue
			}
			// 性質 3
			for k := i + 1; k < j-1; k += 2 {
				if canBeEmpty[i][k] && canBeEmpty[k+1][j] {
					canBeEmpty[i][j] = true
					break
				}
			}
		}
	}

	f := make([]string, n+1)
	for i := n - 1; i >= 0; i-- {
		// 包含 s[i]
		res := string(s[i]) + f[i+1]
		// 不包含 s[i]，注意 s[i] 不能單獨消除，必須和其他字符一起消除
		for j := i + 1; j < n; j += 2 {
			if canBeEmpty[i][j] { // 消除 s[i] 到 s[j]
				res = min(res, f[j+1])
			}
		}
		f[i] = res
	}
	return f[0]
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

func main() {
	s := "zdce"
	result := lexicographicallySmallestString(s)
	fmt.Println(result)
}

在這裏插入圖片描述

Python完整代碼如下：

# -*-coding:utf-8-*-

def is_consecutive(x, y):
    d = abs(ord(x) - ord(y))
    return d == 1 or d == 25

def lexicographically_smallest_string(s):
    n = len(s)
    
    # 初始化 can_be_empty 二維數組
    can_be_empty = [[False] * n for _ in range(n)]
    
    # 初始化空串情況
    for i in range(n - 2, -1, -1):
        can_be_empty[i + 1][i] = True  # 空串
    
    # 填充 can_be_empty 數組
    for i in range(n - 2, -1, -1):
        for j in range(i + 1, n, 2):
            # 性質 2：如果首尾字符相鄰且中間可以清空
            if is_consecutive(s[i], s[j]) and (i + 1 > j - 1 or can_be_empty[i + 1][j - 1]):
                can_be_empty[i][j] = True
                continue
            
            # 性質 3：如果可以被分成兩個可清空的子串
            for k in range(i + 1, j - 1, 2):
                if can_be_empty[i][k] and can_be_empty[k + 1][j]:
                    can_be_empty[i][j] = True
                    break
    
    # 初始化 f 數組
    f = [""] * (n + 1)
    
    # 從後往前計算 f
    for i in range(n - 1, -1, -1):
        # 包含 s[i]
        res = s[i] + f[i + 1]
        
        # 不包含 s[i]，尋找可以消除的區間
        for j in range(i + 1, n, 2):
            if can_be_empty[i][j]:  # 消除 s[i] 到 s[j]
                candidate = f[j + 1]
                if candidate < res:
                    res = candidate
        
        f[i] = res
    
    return f[0]

def abs(x):
    return x if x >= 0 else -x

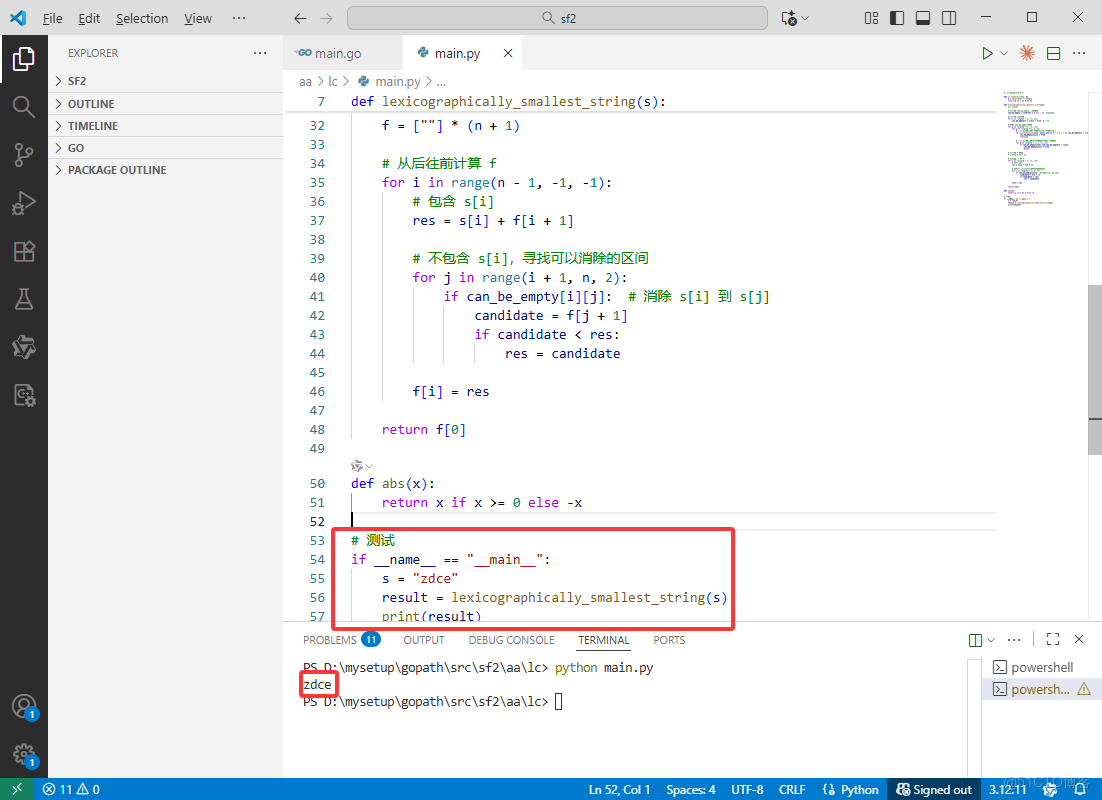
# 測試
if __name__ == "__main__":
    s = "zdce"
    result = lexicographically_smallest_string(s)
    print(result)

在這裏插入圖片描述

C++完整代碼如下：

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <cmath>

using namespace std;

bool isConsecutive(char x, char y) {
    int d = abs(x - y);
    return d == 1 || d == 25;
}

string lexicographicallySmallestString(string s) {
    int n = s.length();

    // 初始化 canBeEmpty 二維數組
    vector<vector<bool>> canBeEmpty(n, vector<bool>(n, false));

    // 初始化空串情況
    for (int i = n - 2; i >= 0; i--) {
        canBeEmpty[i + 1][i] = true; // 空串

        for (int j = i + 1; j < n; j += 2) {
            // 性質 2：如果首尾字符相鄰且中間可以清空
            if (isConsecutive(s[i], s[j]) && (i + 1 > j - 1 || canBeEmpty[i + 1][j - 1])) {
                canBeEmpty[i][j] = true;
                continue;
            }

            // 性質 3：如果可以被分成兩個可清空的子串
            for (int k = i + 1; k < j - 1; k += 2) {
                if (canBeEmpty[i][k] && canBeEmpty[k + 1][j]) {
                    canBeEmpty[i][j] = true;
                    break;
                }
            }
        }
    }

    // 初始化 f 數組
    vector<string> f(n + 1);

    // 從後往前計算 f
    for (int i = n - 1; i >= 0; i--) {
        // 包含 s[i]
        string res = string(1, s[i]) + f[i + 1];

        // 不包含 s[i]，尋找可以消除的區間
        for (int j = i + 1; j < n; j += 2) {
            if (canBeEmpty[i][j]) { // 消除 s[i] 到 s[j]
                string candidate = f[j + 1];
                if (candidate < res) {
                    res = candidate;
                }
            }
        }

        f[i] = res;
    }

    return f[0];
}

int main() {
    string s = "zdce";
    string result = lexicographicallySmallestString(s);
    cout << result << endl;
    return 0;
}

在這裏插入圖片描述

Go語言 , 字符串 , 初始化 , include , 後端開發

0 用戶, 點贊了這篇動態!

福大大架構師每日一題動態日志

@moonfdd

標簽

後端開發 (122)

初始化 (18)

字符串 (11)

include (11)

Go語言 (4)

動態

2025-11-14：移除相鄰字符後字典序最小的字符串。用go語言，給出一個只包含小寫字母的字符串 s。你可以多次（也可以不做任何操作）執行如下步驟：任意選取一對相鄰字符，如果這兩個字母在字母表中相鄰

算法步驟詳細描述

複雜度分析

Go完整代碼如下：

Python完整代碼如下：

C++完整代碼如下：

發表評論

福大大架構師每日一題 動態日志

@moonfdd

標簽

後端開發 (122)

初始化 (18)

字符串 (11)

include (11)

Go語言 (4)

動態

2025-11-14：移除相鄰字符後字典序最小的字符串。用go語言，給出一個只包含小寫字母的字符串 s。你可以多次（也可以不做任何操作）執行如下步驟：任意選取一對相鄰字符，如果這兩個字母在字母表中相鄰

算法步驟詳細描述

複雜度分析

Go完整代碼如下：

Python完整代碼如下：

C++完整代碼如下：

發表 評論

福大大架構師每日一題動態日志

發表評論