計算機如何"看"?
總結一句話:計算機“看”數字,就像人眼看數字一樣,但它用的是像素和數學模型,而不是眼睛和大腦。
- 像素化:一張手寫數字的圖片首先會被分割成一個由微小方塊組成的網格,每個小方塊稱為一個像素。
- 灰度化:對於識別任務,顏色信息通常不重要,所以圖片會被轉換成灰度圖。每個像素不再由RGB三種顏色值表示,而是用一個數值來表示它的灰度強度。通常,0代表純黑色,255代表純白色,中間的值是不同程度的灰色。
- 形成矩陣:現在,這張圖片對計算機來説,就是一個巨大的數字矩陣(或二維數組)。比如,一個28x28像素的圖片,就是一個由784個數字組成的矩陣。
所以,對計算機而言,一個手寫數字“8”並不是一個我們理解的符號,而是一個由784個數字構成的獨特模式。
訓練模型
- 選用數據集: MNIST數據集,包括60,000 張訓練圖,10,000 張測試圖,訓練速度快
-
選用語言:python(運行在pycharm)
1.加載數據集:
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data() print(f" Training images: {len(x_train)}") print(f" Test images: {len(x_test)}") print(f" Image size: {x_train[0].shape} (28x28 pixels)")把機器學習想象成教小孩認數字:
- x_train = 給小孩看的圖片(問題/特徵)
- y_train = 告訴小孩的正確答案(答案/標籤)
- x_test = 給小孩的考試題目(測試問題)
-
y_test = 考試的標準答案(測試答案)
打印結果:
Training images: 60000 Test images: 10000 Image size: (28, 28) (28x28 pixels)2.可視化展示MNIST數據集中的手寫數字樣本:
plt.figure(figsize=(12, 6)) # 創建畫布,設置大小12x6英寸 print(" Showing first 12 digits from training set...") for i in range(12): plt.subplot(3, 4, i + 1) # 創建3行4列的子圖,當前是第i+1個 plt.imshow(x_train[i], cmap='gray') # 顯示第i張訓練圖片,用灰度色彩 plt.title(f'Digit: {y_train[i]}', fontsize=12) # 設置標題為真實標籤 plt.axis('off') # 關閉座標軸,讓圖片更乾淨 plt.suptitle('MNIST Handwritten Digits Samples', fontsize=16, fontweight='bold') plt.tight_layout() # 自動調整子圖間距,避免重疊顯示情況:
3.數據預處理中的歸一化操作:
x_train = x_train / 255.0 x_test = x_test / 255.0數據歸一化的目的:
① 大數值會導致訓練不穩定,如果輸入都很大(0~255),梯度也會很大,會讓模型震盪、難以收斂。
② 這是圖像處理領域的標準做法,幾乎所有深度學習任務都要做歸一化(normalization)。4.搭建簡單的神經模型:
model = tf.keras.Sequential([ # 把 28x28 的二維圖片拉成一條 784 長度的向量,方便神經網絡處理 tf.keras.layers.Flatten(input_shape=(28, 28)), # 全連接層:128 個神經元,用 ReLU 激活,負責提取特徵 tf.keras.layers.Dense(128, activation='relu'), # 輸出層:10 個神經元,對應數字 0~9,softmax 輸出每個數字的概率 tf.keras.layers.Dense(10, activation='softmax') ]) # 編譯模型:選擇優化器、損失函數、評估指標 model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])打印內容:
Model: "sequential" ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ flatten (Flatten) │ (None, 784) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense (Dense) │ (None, 128) │ 100,480 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_1 (Dense) │ (None, 10) │ 1,290 │ └─────────────────────────────────┴────────────────────────┴───────────────┘ Total params: 101,770 (397.54 KB) Trainable params: 101,770 (397.54 KB) Non-trainable params: 0 (0.00 B) -
flatten (譯為壓扁):
- 作用:把28×28的圖片壓平成784個像素點的一維數組,
- 輸出形狀:(None, 784),None = 批處理大小(可以是任意數量,比如32、64張圖片一批);784 = 28×28 個像素點
- 參數數量:0(只是重排操作,沒有可學習的參數)
-
dense:
- 作用:全連接層,128個神經元
- 輸出形狀:(None, 128)(每張圖片輸出128個特徵值)
- 參數數量:100,480個可學習參數,
- 參數計算 = (輸入維度 × 輸出維度) + 輸出維度偏置的個數,,有了偏置,神經元可以“整體平移”,即使輸入為 0 也可以輸出非零值。
-
dense_1:
- 作用:輸出層,10個神經元(對應0-9十個數字)
- 輸出形狀:(None, 10)(每張圖片輸出10個概率值)
-
參數數量:1,290個可學習參數
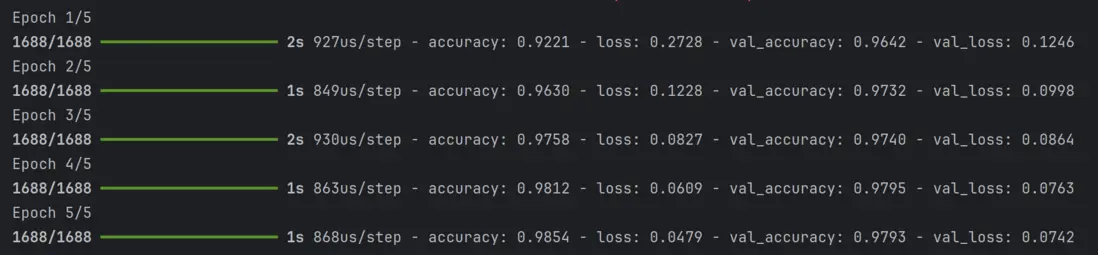
5.訓練模型:
history = model.fit(x_train, y_train, epochs=5, # 5次完整遍歷訓練集 batch_size=32, # 5次完整遍歷訓練集 validation_split=0.1, # 把訓練數據的 10% 自動劃分為驗證集 verbose=1)訓練過程:
6.驗證模型是否能真正的識別數字:
plt.figure(figsize=(15, 8)) # 隨機挑 12 張(不會重複) indices = np.random.choice(len(x_test), 12, replace=False) for i, idx in enumerate(indices): plt.subplot(3, 4, i + 1) test_image = x_test[idx] true_label = y_test[idx] prediction = model.predict(np.array([test_image]), verbose=0) # 讓模型預測這張圖片屬於 0~9 中哪一個 predicted_label = np.argmax(prediction) # 找到概率最大的數字,就是預測值 confidence = np.max(prediction) # 模型對該預測的置信度(0~1) plt.imshow(test_image, cmap='gray') # Check if prediction is correct if predicted_label == true_label: color = 'green' result = "✓ Correct" else: color = 'red' result = "✗ Wrong" plt.title(f'True: {true_label} | Pred: {predicted_label}\n{result} | Conf: {confidence:.2f}', color=color, fontsize=10) plt.axis('off') plt.suptitle('Model Prediction Results (Green=Correct, Red=Wrong)', fontsize=16, fontweight='bold') plt.tight_layout()驗證結果:
至此一個簡潔的識別模型已經訓練完成!
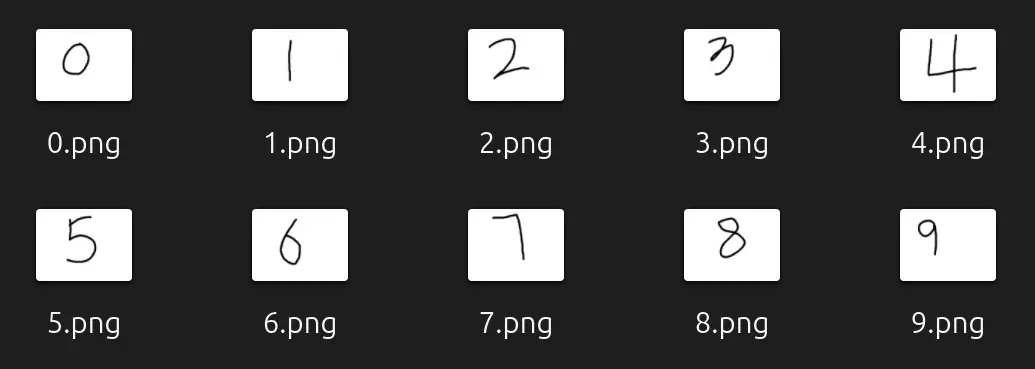
使用訓練的模型識別我的手寫圖片
我利用Krita手寫了0-9的圖片,如下:
def recognize_digit(image_path):
"""從圖像文件中識別數字(使用 PIL)"""
try:
# 使用 PIL 讀取圖像
img = Image.open(image_path)
# 如果不是灰度圖,先轉成灰度圖(MNIST 是單通道灰度)
if img.mode != 'L':
img = img.convert('L')
print(f"📊 原始圖片尺寸: {img.size}")
# 將圖像調整為 28x28(MNIST 模型輸入尺寸)
img_resized = img.resize((28, 28), Image.Resampling.LANCZOS)
# 轉成 numpy 數組
img_array = np.array(img_resized)
# 自動檢測白底黑字或黑底白字
# MNIST 是“白底黑字”,如果平均值偏亮,就反色
if np.mean(img_array) > 128:
img_array = 255 - img_array
print("🔄 已檢測到白底,自動反色為 MNIST 格式")
# 像素歸一化到 0-1
img_normalized = img_array / 255.0
# 打印 ASCII 預覽,輔助觀察模型看到的內容
print("\n📱 處理後的圖像(ASCII 預覽):")
print_preview(img_normalized)
# 進行預測(模型要求輸入 shape 為 (1,28,28))
prediction = model.predict(np.array([img_normalized]), verbose=0)
# 找出概率最大的數字
predicted_digit = np.argmax(prediction)
# 獲取最大概率作為置信度
confidence = np.max(prediction)
print(f"\n🎯 Prediction Result:")
print(f" 🤖 預測數字: {predicted_digit}")
print(f" 📈 置信度: {confidence:.2%}")
print(f" 📁 文件名: {os.path.basename(image_path)}")
# 輸出所有數字的概率
print(f"\n📊 All digit probabilities:")
for i, prob in enumerate(prediction[0]):
if prob > 0.01: # Only show probabilities > 1%
marker = "🎯" if i == predicted_digit else " "
print(f" {marker} Digit {i}: {prob:.2%}")
# 輸出置信度等級
print(f"\n💪 置信度等級: ", end="")
if confidence > 0.9:
print("⭐⭐⭐⭐⭐ (非常高)")
elif confidence > 0.7:
print("⭐⭐⭐⭐ (較高)")
elif confidence > 0.5:
print("⭐⭐⭐ (一般)")
else:
print("⭐ (很低)")
return predicted_digit, confidence
except Exception as e:
print(f"❌ 錯誤: {e}")
return None
這裏以數字2為例打印結果:
📱 Processed Image (ASCII preview):
--==--
==##**==++++
**++.. ++
**-- ++
.. ++
++
++
::==
==::
**
++--
..** ::::..
++..--**##****++
**%%****::
++@@==..
--##..
--
🎯 Prediction Result:
🤖 預測數字: 2
📈 置信度: 95.47%
📁 文件名: 2.png
📊 All digit probabilities:
🎯 Digit 2: 95.47%
Digit 3: 1.54%
Digit 8: 1.56%
💪 置信度等級: ⭐⭐⭐⭐⭐ (非常高)結語
至此,一個小型的圖像識別基本完成,但是並不是所有的手寫數字置信度等級都可以達到這麼高,僅僅依靠這個小的模型,還是遠遠不夠的,接下來會嘗試利用CNN(卷積神經網絡)來進行訓練。由於不太懂得這方面的專業知識,可能會存在很多問題,歡迎留言,我會積極改正!