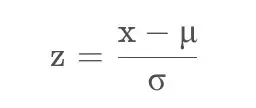一、背景

在穩定性保證中，重要的一個環節就是故障管理體系建設，故障管理體系的四大核心功能——故障發現、故障觸達、故障定位和故障恢復，其中故障發現作為故障管理的第一步至關重要，包含了指標預測、異常檢測和故障預測等方面，主要目標是能及時、準確地發現故障。今天主要針對故障發現環節中的異常檢測介紹AI異常檢測算法在指標檢測上的應用。

傳統基於閾值的異常檢測方法的缺點：

• 比較依賴個人經驗，需要了解指標的歷史趨勢。
• 配置比較複雜，有時對週期波動型的時序數據還要針對不同的時間段配置不同的閾值。
• 隨着業務的變更要不斷調整閾值，隨着時間推移、業務的變更，觀測指標趨勢也可能發生改變，要對閾值做相應的調整。

受大促或異常值影響比較大，像有些閾值配置同比或者環比，如果上一時刻或者歷史同時刻有數據有異常，會影響該時刻的檢測判斷。

對比固定閾值的檢測，AI檢測算法在突增、突降等異常檢測場景中可以很好地解決上述問題。下面會針對AI檢測算法在可觀測性產品中的應用做相關的介紹。

二、異常檢測算法

AI異常檢測算法之前，通常需要對歷史數據做預處理，包括異常值的剔除，缺失值的填充等。

異常值剔除

這時可能大家會有疑惑，做異常檢測為什麼還要剔除異常值，這裏的異常值是指作為參照的歷史數據中的極值，剔除極值可以減少極值影響，去除異常值有助於提高異常檢測算法的準確性。

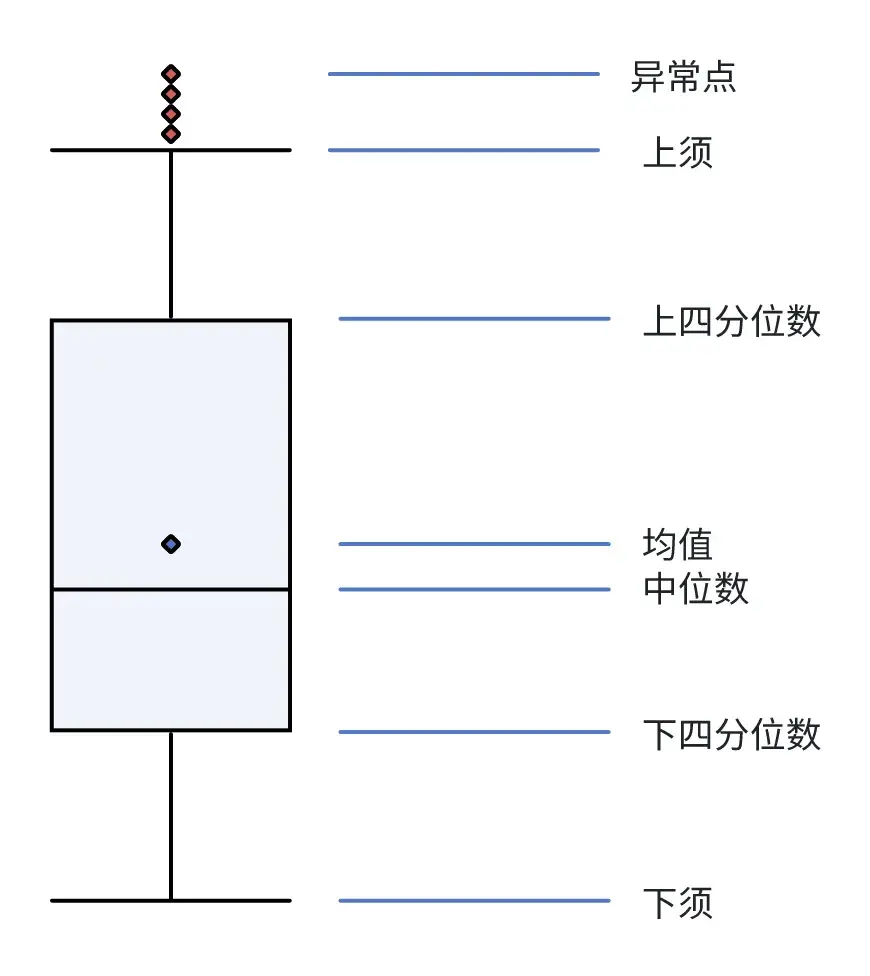
箱型圖

箱型圖不需要考慮數據集的分佈情況，它是通過將數據分成四分位來衡量統計分散度和數據可變性，是一種簡單有效的異常點剔除算法。

• 下四分位數：25%分位點對應的值（Q1）
• 中位數：50%分位點對應的值（Q2）
• 上四分位數：75%分位點對應的值（Q3）
• 上須：Q3+1.5（Q3-Q1）
• 下須：Q1-1.5（Q3-Q1）

如上圖所示，大於上須的值或者小於下須的值我們認為是異常值。

考慮3sigma跟箱型圖算法的特點，箱型圖可能更加具普適性，因為它不用考慮數據集的分佈情況，在實際應用中我們也是採用的箱型圖算法來剔除異常點。剔除異常值後需要對缺失值進行填充，確保數據的連續性，防止後續檢測算法在處理時報錯，通常缺失值填充的方法有：

• 前後填充法，使用前一個值填充或者後一個正常值填充。
• 均值、中位數填充法。
• 插值法，插值法有線性插值和多項式插值。線性插值就是通過線性迴歸預測缺失位置的值，多項式插值使用多項式迴歸預測缺失位置值。

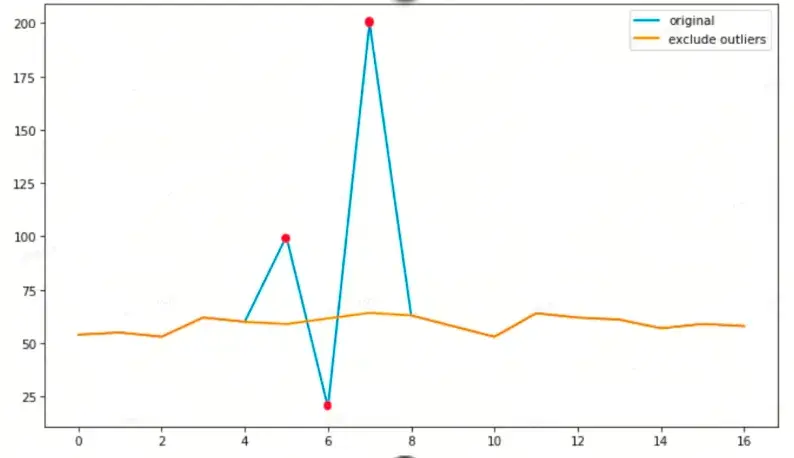
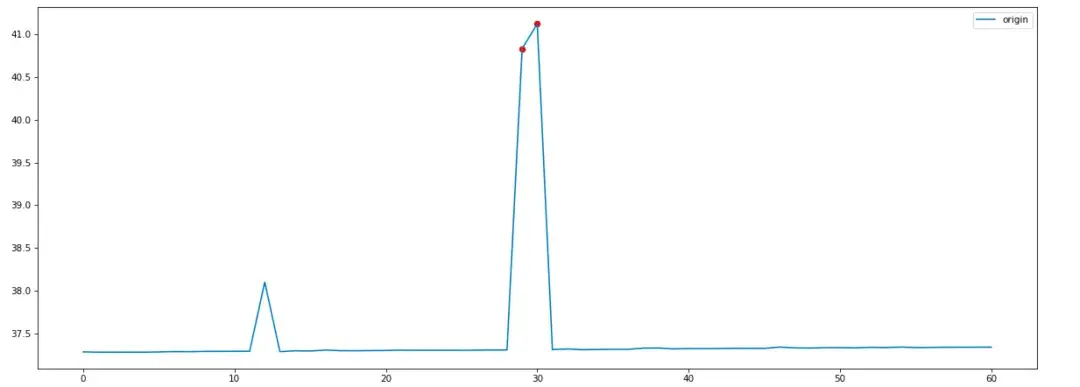
下面是我們採用箱型圖剔除異常點並採用多項式插值的效果：

藍色的線是原始的觀測值，紅色的點是檢測出的異常點，黃色的線是通過插值法填充後的結果。數據預處理後，利用預處理後的結果進行異常點檢測。

統計方法的應用

對觀測數據進行分析，大部分的指標有周期性和趨勢性。

可觀測性產品中異常檢測主要採用的統計方法，包括3sigma和zscore變點檢測算法。

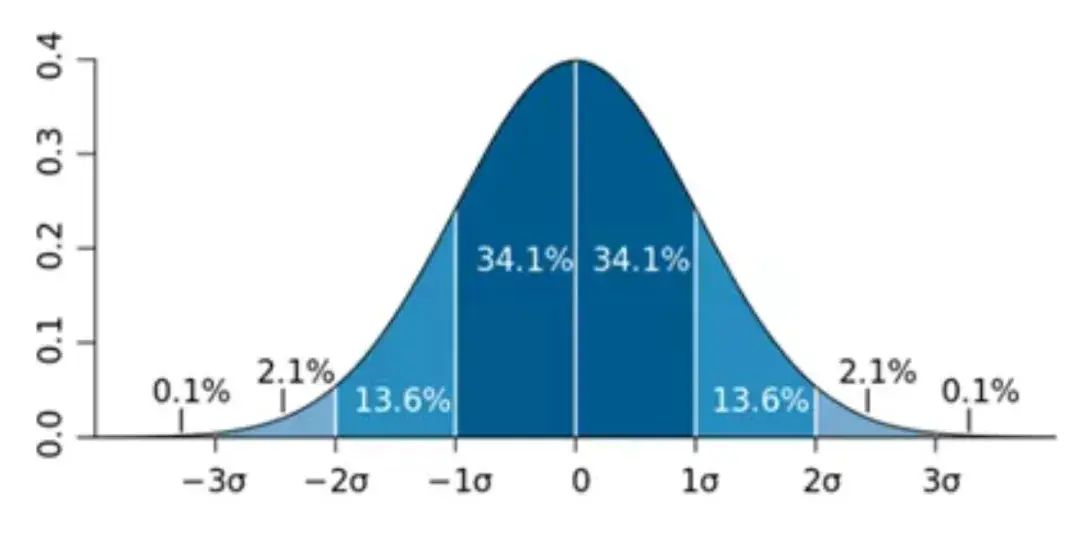
3sigma算法

3sigma算法是考慮如果數據集分佈屬於正態分佈，數據點落在偏離均值正負1倍標準差（即sigma值）內的概率為68.2%；數據點落在偏離均值正負2倍標準差內的概率為95.4%；數據點落在偏離均值正負3倍標準差內的概率為99.6%，意思是數據點落在偏離均值正負3倍標準差之外的概率非常小，可以認為這些數據點為極端異常點。通過下面的標準正態分佈的概率密度圖可以很好地理解該算法。

通過觀察發現，可觀測性平台的大部分指標，從時間緯度縱向分析（歷史同一時刻）符合正態分佈，但橫向來看並不符合正態分佈。

以創建訂單QPS指標為例，獲取過去60天同一時刻10點整的QPS觀測數據，通過Python繪製直方圖，並通過KS算法做正態分佈驗證：

從直方圖上看數據基本符合正態分佈，用KS算法驗證得到pvalue，pvalue>0.05符合正態分佈特徵。

所以我們可以採用3sigma算法對絕大部分指標做縱向的異常點檢測。

接下來我們橫向分析數據的分佈情況，首先分析完整一天的數據是否符合正態分佈，以訂單QPS為例：

按照上述的方法繪製直方圖，並通過KS算法驗證是否符合正態分佈。

從直方圖上看橫向看QPS指標並不符合正態分佈。用KS算法驗證得到pvalue，pvalue<0.05所以不符合正態分佈。

接下來分析連續30個點的數據，看是否符合正態分佈。還是以創建訂單QPS為例，獲取11:31:00～12:03:00時間點的數據繪製直方圖。

從圖形上看基本符合正態分佈情況，KS算法檢測是否是正態分佈，可以看到連續30個點數據集符合正態分佈。

結合上述分析，我們對觀測指標的檢測分為兩步：

• 縱向，獲取歷史同一時刻30個點的觀測值，通過3sigma算法來檢測異常。
• 橫向，zscore算法進行變點檢測，橫向獲取某個時刻往前歷史30個點的觀測值。

最後，藉助縱向和橫向檢測結果聯合決策某個點是否異常。

zscore 算法

橫向異常檢測我們採用zscore算法，橫向檢測我們採用過去30個點的數據，具體做法：

• 過去30個點數據按窗口做平滑處理，窗口大小為3；
• 平滑後的數據前後做差值；
• 對差值數據集計算zscore，zscore的計算公式為：

• 使用正態分佈生存函數計算zscore的右尾概率，判斷概率是否大於0.01，小於0.01則為異常。

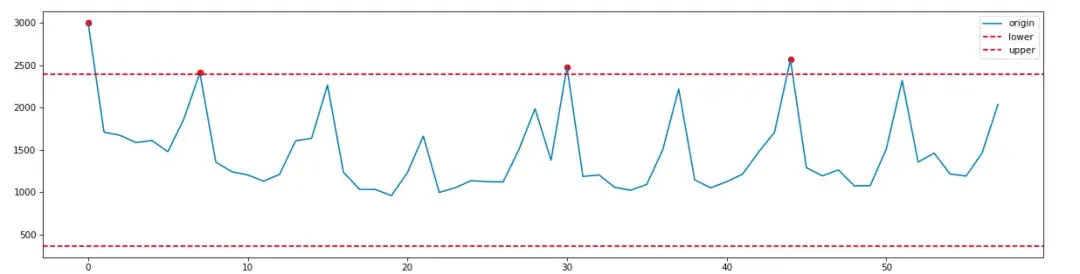
以創建訂單QPS為例，獲取2024-01-15 14:00:00點歷史30天同一時刻的值使用3sigma檢測邏輯為：

使用zscore算法檢測2024-01-14 11:31:00～2024-01-14 12:03歷史32個點的異常情況如下：

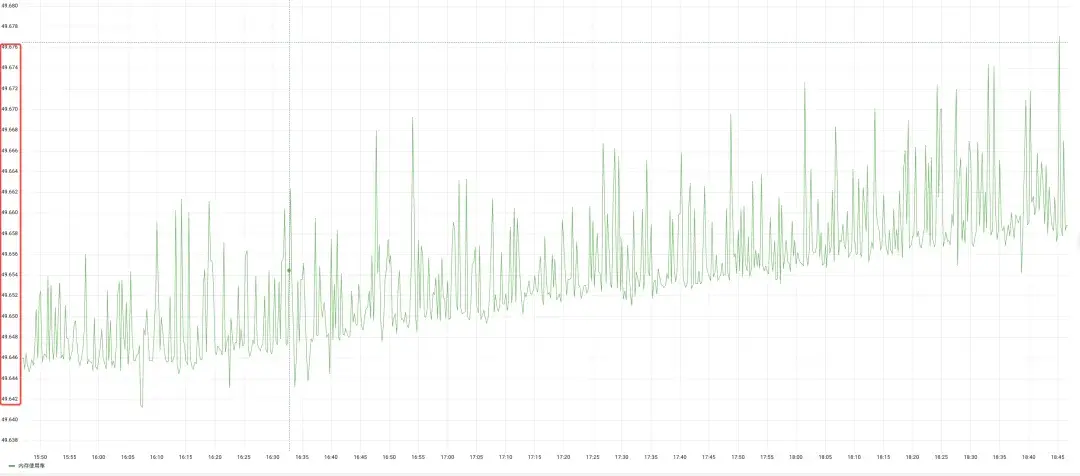
以上橫向和縱向的算法可以解決大部分的觀測指標的異常檢查，但是像有些指標波動一直都特別小，如內存指標，見下圖：

使用3sigma統計方法檢測異常點得到如下結果：

可以看到3sigma計算的上下限非常小，上下限接近1左右，這導致這種指標的檢測異常點非常多。因此，我們探索使用其他複雜的算法，比如機器學習的算法來解決。

機器學習方法的應用

異常檢測統計方法對於某些特殊場景可能存在檢測誤差大、噪音多等問題，所以我們探索了機器學習檢測算法，考慮到觀測數據大多是沒有標註的，而且獲取標註的成本也比較高，我們主要考慮無監督的算法，針對孤立森林做了研究和應用。

孤立森林

孤立森林算法，一種適用於連續數據的無監督異常檢測方法。該算法不借助類似距離、密度（LOF，K-means）等指標去描述樣本與其他樣本的差異，而是直接去刻畫所謂的疏離程度（isolation），因此該算法簡單、高效。而且該算法魯棒性高且對數據集的分佈無假設。

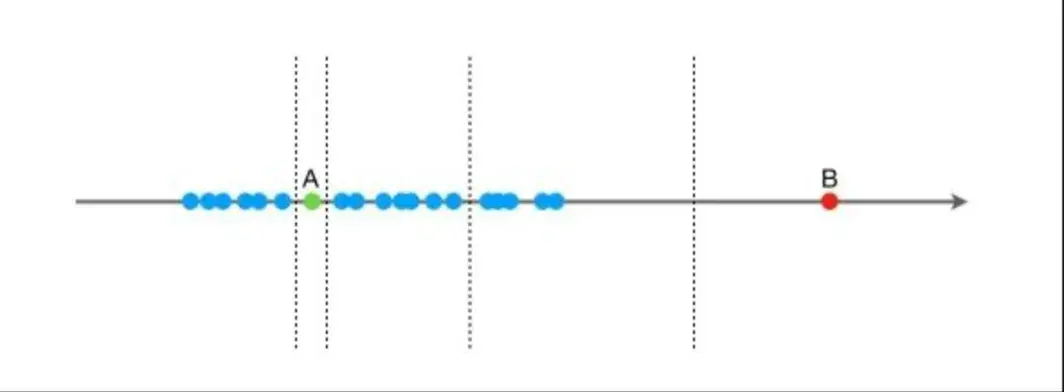
孤立森林算法的思想：假設現在有一組一維數據（如下圖），我們要對這組數據進行切分，目的是把點A和B單獨切分出來，先在最大值和最小值之間隨機選擇一個值X，然後按照=X可以把數據分成左右兩組，在這兩組數據中分別重複這個步驟，直到數據不可再分。點B跟其他數據比較疏離，可能用很少的次數就可以把它切分出來，點A跟其他數據點聚在一起，可能需要更多的次數才能把它切分出來。那麼從統計意義上來説，相對聚集的點需要分割的次數較多，比較孤立的點需要的分割次數少，孤立森林就是利用分割的次數來度量一個點是聚集的（正常）還是孤立的（異常）。

在實際應用中Python sklearn已經對孤立森林算法做了支持，我們只需要對算法中的參數做些調整就可以。sklearn IsolationForest算法的參數包括：

• n_estimators：int，optional（default=100），iTree的個數，指定該森林中隨機樹數量。
• max_samples：int or float，optional（default="auto"）構建子樹的樣本數，整數為個數，小數為佔全集的比例，用來訓練隨機數的樣本數量。
• contamination：float in（0，0.5），optional（default=0.1）表示異常數佔給定數據集的比例，數據集中污染的數量，其實就是訓練數據中異常數據的數量，定義該參數值作用是決策函數中定義閾值。
• max_features：int or float，optional （default=1.0）構建每個子樹的特徵數，整數位個數，小數為佔全特徵的比例，指定從總樣本X中抽取來訓練每棵樹iTree的屬性的數量，默認只使用一個屬性，如果設置為int整數，則抽取max_features個屬性；如果是float浮點數，則抽取max_features * X.shape[1]個屬性。
• bootstrap：boolean，optional （default=False）採樣是有放回還是無放回，如果為True，則各個樹可放回地對訓練數據進行採樣。如果為False，則執行不放回的採樣。
• n_jobs：int or None，optional （default=None） 在運行fit（）和predict（）函數時並行運行的作業數量。除了在joblib.parallel_backend上下文的情況下，None表示為1。設置為-1則表示使用所有可用的處理器Random_State : int， RandomState instance or None， optional （default=None）每次訓練的隨機性，如果設置為int常數，則該Random_State參數值是用於隨機數生成器的種子；如果設置為RandomState實例，則該Random_State就是一個隨機數生成器 如果設置為None，該隨機數生成器就是使用在np.random中的RandomState實例。
• verbose：int，optional （default=0）訓練中打印日誌的詳細程度，數值越大越詳細。
• warm_start：bool，optional （default=False）當設置為True時，重用上一次調用的結果去fit，添加更多的樹到上一次的森林1集合中；否則就fit一整個新的森林。

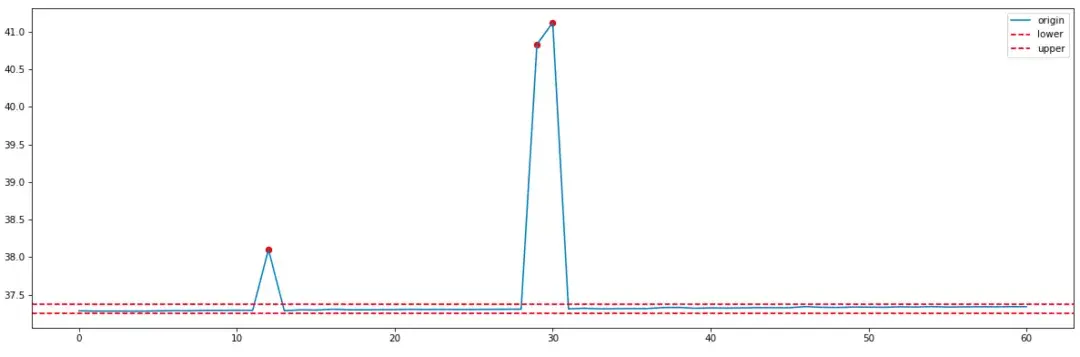
我們主要調整contaimination來控制異常檢測算法的閾值大小，實際應用中我們定義contamination值為0.01，相對比較嚴格的檢測閾值。針對統計算法中檢測波動比較小的內存使用率，再用孤立森林做檢測得到的結果如下：

對比3sigma統計算法，孤立森林相對檢測更加嚴格，像index為12的突刺異常噪音點沒有被檢測出來。

統計算法相對機器學習算法算法複雜度低，檢測速度快，而且具有比較強的解釋性，而機器學習算法跟統計算法比魯棒性更強對數據集的分佈沒有要求，但是解釋性比較低。結合兩類算法的優缺點我們通用的異常檢測策略中會結合兩種檢測算法做聯合決策，來提高檢測的準確性。

深度學習方法的應用

另外，針對一些核心場景，比如登陸、商品詳情、下單、供應鏈等這些場景，要求預測的準確性要特別高，同時告警噪音小，我們在深度學習算法領域也做了些探索，像LSTM、transformer，其中主要針對近期熱門的transformer模型以及變種進行了探索和實驗，最終通過實驗採用了效果相對比較好的pyraformer。pyraformer使用了金字塔結構的注意模塊，可以很好地捕獲長期依賴性，同時有較小的時間複雜度和空間複雜度，具體關於pyraformer的理論介紹，感興趣的可以參考pyraformer相關論文或文章，這裏只介紹我們對pyraformer做的一些小改動。

我們採用pyraformer做指標預測的方式主要是基於預測值計算上下限，開源的pyraformer是不支持上下限預測的，具體的做法是：

• 通過預測歷史時刻的預測值，同觀測值做差值計算，計算結果作為一個新的誤差指標寫入到時序數據庫中。
• 預測未來某個時刻的值時，通過第一步的誤差指標獲取最近的30個點誤差值，計算30個誤差點的標準差作為sigma，然後該時刻的預測值加減3倍的sigma就計算得到了上下限。

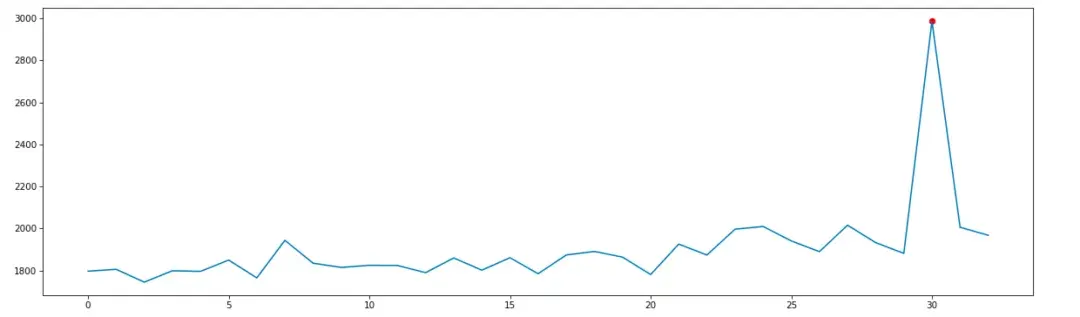
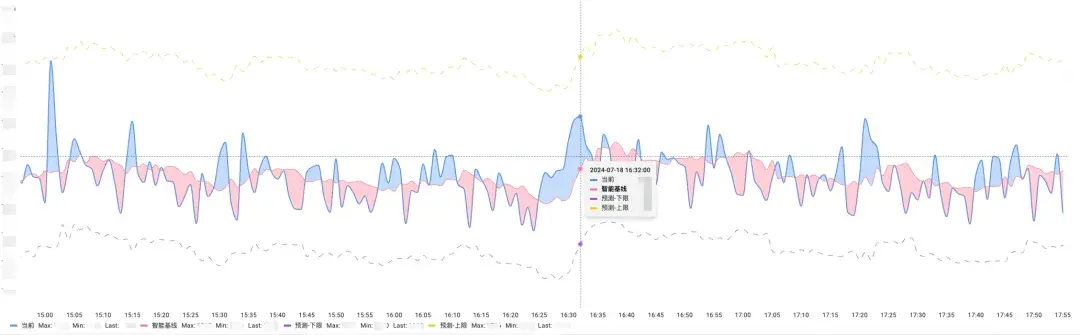
下圖為某個核心場景的預測效果：

目前該算法已經應用到了50+個核心場景的日常告警中，算法應用之後，核心場景的告警誤報減少了 50%以上。

三、總結和展望

目前，異常檢測算法主要應用在兩個方面，一個是核心場景風險感知場景，主要檢測應用的QPS的突增&突降檢測、RT、錯誤率、錯誤碼、異常數、CPU、內存的突增檢測場景中，異常檢測準確率達90%以上；另一個是在應用發佈變更的風險感知場景，在發佈批次結束，針對變更後的實例檢測、RT、錯誤率、異常數等有無突增異常，防止問題代碼發佈上線造成更大的影響。未來我們會持續在AI檢測算法和預測算法上進行研究，並在更多場景落地。另外，我們在故障觸達、故障定位方面也在做探索，在一些場景上取得了較好的效果，後續會單獨拿出來做分享。

*文 / 雲斌

本文屬得物技術原創，更多精彩文章請看：得物技術

未經得物技術許可嚴禁轉載，否則依法追究法律責任！