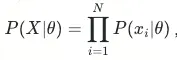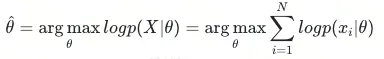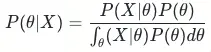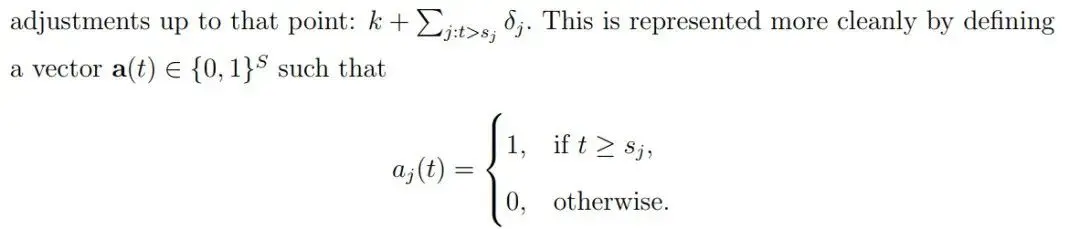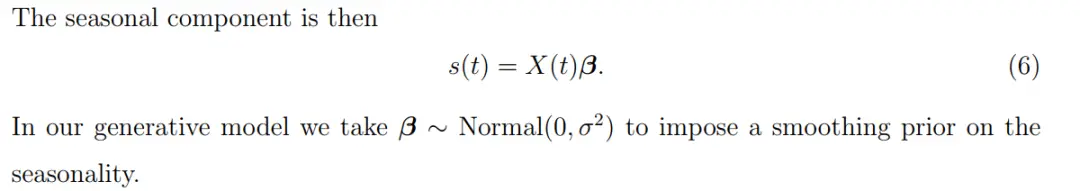隨着得物業務的快速發展，積累了大量的時序數據，這些數據對精細化運營，提升效率、降低成本有着重要作用。在得物的時序數據挖掘場景中，時序預測Prophet模型使用頻繁，本文對Prophet的原理和源碼進行深入分析，歡迎閲讀和交流。

一、引入

時間序列是指按照時間先後順序收集或觀測的一系列數據點，這類數據通常都具有一定時間相關性，基於這種順序性，我們可以對時間序列進行多種數據挖掘任務，包括分類、聚類、異常檢測和預測等。

時序任務在許多領域都有廣泛的應用，包括金融、商業、醫療、氣象、工業生產等。在得物的業務場景中，應用最為廣泛的是時序預測問題，本文介紹的內容主要和時序預測相關。

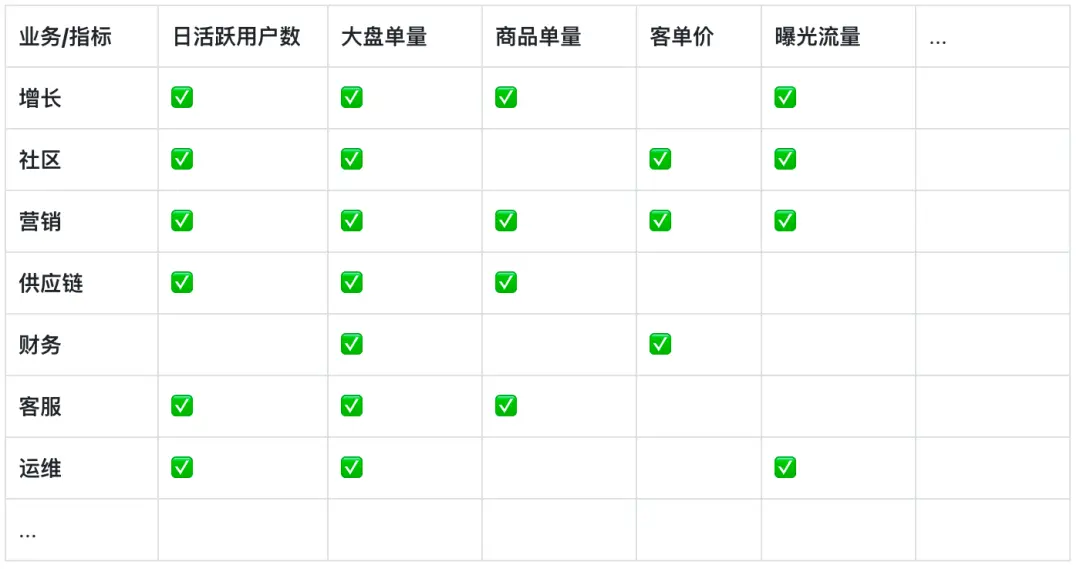
時序預測利用歷史時間序列數據構建數學統計、機器學習或深度學習等模型，來預測未來的觀測值，其目的是為了對時間序列的趨勢、週期性、季節性、特殊事件等規律進行捕捉並預測，從而指導業務人員做出商業、運營決策。以下是時間序列預測在得物各業務域的需求情況，總之哪裏有指標，哪裏就有預測。

解決時序預測問題的算法研究歷史非常悠久，是備受關注和持續發展的領域。根據算法原理和方法進行分類，時序預測模型可以分為以Holt-winters，ARIMA為代表的經典統計模型，用單一時序變量進行參數擬合；以線性迴歸、樹迴歸為代表的傳統機器學習算法，在有監督學習的框架下，構建特徵來預測目標值；以及運用CNN、RNN、Transform等特徵提取器，在Encoder-Decoder框架下進行預測的深度學習方法。

本文將介紹的Prophet模型和上述三種分類算法有所差異，但方法和原理上也結合了參數擬合、機器學習的思想，它將時序分解成趨勢變化、季節性、節假日、外部迴歸因子之和，是結合時序分解的加法模型預測算法。

Prophet於2017年由Facebook’s Core Data Science team開源發佈，儘管從時間上來看不是很新的模型，但是在得物實際的時序預測場景中取得了不俗的效果。目前網上的博客主要介紹了模型的基本原理、使用方式，在使用過程中筆者仍有一些疑問，例如：

• Prophet模型是如何進行訓練和預測？
• 模型如何進行概率預測，得到預測的上界和下界？

筆者帶着這些問題閲讀了Prophet的源碼，發現了一些論文中沒有提到的細節和流程，對以上問題有了答案，這裏分享給大家。代碼參考Prophet python語言實現版本v1.1.5。

二、準備知識

如果讀者有機器學習基礎，熟悉最優化計算方法、貝葉斯估計、MCMC採樣可以跳過這一小節，不熟悉的讀者可以按照這一小節提到的概念搜索相關資料。

參數估計

通俗的説預測就是利用已知數據來推測產生該數據的模型和參數，然後用推測的模型和參數產生下一個結果。對於模型的參數估計方法，有頻率學派和貝葉斯學派之分。頻率學派認為模型參數是個固定的值。而貝葉斯學派是認為模型參數不是一個固定的值，而是源自某種潛在分佈，希望從數據中推知該分佈。

用大家最熟悉的線性迴歸為例，假設噪聲服從正態分佈：

在概率視角下，線性迴歸可以表示為：

其中θ=(w0,w,σ^2)是模型所有的參數。

在頻率學派視角下θ是一個常量，可以用極大似然估計來估計參數值。其思想是對於N個觀測樣本來説使得其發生概率最大的參數就是最好的參數。整個觀測集發生的概率為：

由於連乘不容易參數求解，可以採用最大對數似然方法，線性迴歸有解析解，我們可以直接求導計算得到最優的θ_hat：

在貝葉斯學派視角下θ是一個隨機變量而不是一個固定的值，由一個先驗分佈進行約束，通過利用已知樣本進行統計推斷。貝葉斯學派認為一個好的θ不僅要考慮似然函數P(X|θ)還要考慮θ的先驗分佈P(θ)，即最大化P(X|θ)P(θ)。由於X的先驗分佈是固定的常數，最大化函數可以寫成P(X|θ)P(θ)/P(X)，根據貝葉斯公式可知P(X|θ)P(θ)/P(X)=P(θ|X)，即找到一個θ_hat能夠最大化後驗概率P(θ|X)。

求解參數θ可以選擇使用最大後驗估計（Maximum A Posterior, MAP）或者貝葉斯估計兩種方法，最大後驗估計直接求解讓後驗概率最大的θ。這樣問題就轉化還成一個約束問題，實際中可以使用梯度下降、牛頓法或者L-BFGS擬牛頓法等數值優化方法進行求解。

從最大似然估計和最大後驗估計來看求解的參數θ是一個確定值，但貝葉斯估計不是直接估計θ，而是估計θ的分佈。在最大後驗估計中由於求θ極值過程中與P(X)無關，分母可以被忽略。但是在貝葉斯估計中是求整個後驗概率的分佈，分母不能忽略。對於連續型隨機變量有：

則貝葉斯公式變為：

分母是積分形式一般沒有解析解，直接計算是非常困難的。於是引入馬爾可夫鏈蒙特卡洛算法（Markov Chain Monte Carlo, MCMC）進行採樣，從而得到各個參數的一系列採樣值。

Stan開源框架

https://mc-stan.org/ : Stan is a state-of-the-art platform for statistical modeling and high-performance statistical computation.

Stan是一個用於貝葉斯統計建模和推斷的開源框架，包含了定義概率模型的編程語言，以及高效執行貝葉斯推斷的算法庫，被廣泛用於統計建模和機器學習任務，它集成了上文談到的MAP、MCMC等求解算法，在Python中可以通過PyStan包來使用 Stan。

Prophet基本原理

Prophet基於時間序列分解和參數擬合來實現高效的訓練和預測。首先Prophet定義了一個關於時間步t的加法函數，函數值由趨勢項、季節項、節假日項、外部因子項以及觀測噪聲組成，核心公式如下：

其中g(t)代表趨勢項，s(t)代表季節項，h(t)代表節假日項（泛指外部迴歸變量），ε_t代表誤差項。具體各項公式可以參考附錄中的文章以及官方論文。其中季節項、節假日項、外部因子項可以統一視為迴歸因子，除了構造特徵的方法不同以外，在模型訓練和預測階段都是一樣的處理方法。

Prophet其實是一種廣義線性模型，其數學形式是：

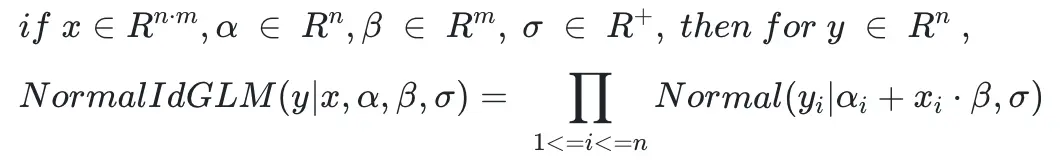
其中y是歷史label數據，x是Prophet中的加法迴歸因子變量，α是趨勢項*（1+乘法迴歸因子變量），β是迴歸因子的權重，σ是噪聲服從高斯分佈。模型訓練的就是公式中未知參數，Prophet的python代碼負責數據輸入、預處理、流程控制、可視化等部分功能，核心算法求解模塊調用Stan進行求解。Stan有自己定義的一套語言體系，定義了變量、輸入數據和模型，Prophet數學模型轉化成Stan的建模語言如下表示：

• 變量和數據

data {
  int T;                // Number of time periods
  int<lower=1> K;       // Number of regressors
  vector[T] t;          // Time
  vector[T] cap;        // Capacities for logistic trend
  vector[T] y;          // Time series
  int S;                // Number of changepoints
  vector[S] t_change;   // Times of trend changepoints
  matrix[T,K] X;        // Regressors
  vector[K] sigmas;     // Scale on seasonality prior
  real<lower=0> tau;    // Scale on changepoints prior
  int trend_indicator;  // 0 for linear, 1 for logistic, 2 for flat
  vector[K] s_a;        // Indicator of additive features
  vector[K] s_m;        // Indicator of multiplicative features
}

• 模型

model {
  //priors
  k ~ normal(0, 5);
  m ~ normal(0, 5);
  delta ~ double_exponential(0, tau);
  sigma_obs ~ normal(0, 0.5);
  beta ~ normal(0, sigmas);


  // Likelihood
  y ~ normal_id_glm(
    X_sa,
    trend .* (1 + X_sm * beta),
    beta,
    sigma_obs
  );
}

論文中各項成分的參數預先設定了先驗分佈，根據：

能夠得到後驗概率，根據第二部分提到的參數估計方法，運用最大後驗估計或MCMC採樣即可得到參數估計值。

三、Prophet源碼剖析

代碼結構

Prophet代碼目錄如下所示，核心邏輯主要是Prophet.stan、models.py 、 forecaster.py三個腳本，本文的分享主要圍繞這三個腳本。

|-- stan
    |-- Prophet.stan # stan語言實現的Prophet模型
|-- setup.py
|-- Prophet
    |-- serialize.py # Prophet訓練完成的模型的序列化、模型的存儲和加載，以便後續重用。
    |-- plot.py # 可視化模塊
    |-- models.py # stan模型定義
    |-- diagnostics.py # 用於診斷 Prophet 模型性能的函數，比如計算誤差指標、繪製診斷圖等。
    |-- tests # 封裝的測試腳本
    |-- __init__.py
    |-- __version__.py
    |-- forecaster.py #  Prophet 類的定義，模型的核心邏輯，數據的處理、模型的擬合和預測等功能
    |-- utilities.py # 包含了一些輔助函數，用於處理時間序列數據、特徵工程等。
    |-- make_holidays.py # 節假日具體日期的構造

• Prophet.stan：用Stan編程語言實現的Prophet模型腳本。
• models.py：python和Stan語言交互的模塊，定義使用Stan腳本語言時的輸入數據，擬合參數、輸出數據，控制Stan進行參數擬合、採樣。
• forecaster.py：Prophet模型核心代碼，定義了Prophet類，涉及整個模型的數據處理、模型訓練和模型推理等功能。

模型框架

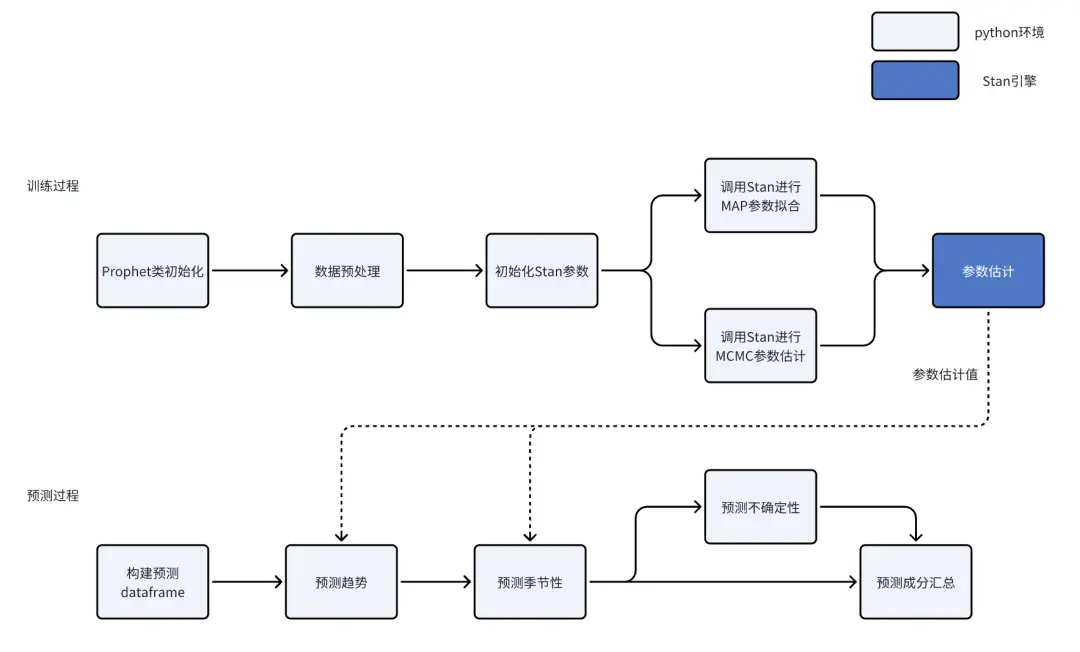
Prophet模型訓練-預測流程如下所示：

初始參數

• Prophet類初始化初始化模塊主要是讀取預先設定和Prophet有關的模型參數。分別有以下幾類：
• • 趨勢項相關

growth: String 'linear', 'logistic' or 'flat' to specify a linear, logistic or
    flat trend.
changepoints: List of dates at which to include potential changepoints. If
    not specified, potential changepoints are selected automatically.
n_changepoints: Number of potential changepoints to include. Not used
    if input `changepoints` is supplied. If `changepoints` is not supplied,
    then n_changepoints potential changepoints are selected uniformly from
    the first `changepoint_range` proportion of the history.
changepoint_range: Proportion of history in which trend changepoints will
    be estimated. Defaults to 0.8 for the first 80%. Not used if
    `changepoints` is specified.
changepoint_prior_scale: Parameter modulating the flexibility of the
    automatic changepoint selection. Large values will allow many
    changepoints, small values will allow few changepoints.

• • 季節性相關

yearly_seasonality: Fit yearly seasonality.
    Can be 'auto', True, False, or a number of Fourier terms to generate.
weekly_seasonality: Fit weekly seasonality.
    Can be 'auto', True, False, or a number of Fourier terms to generate.
daily_seasonality: Fit daily seasonality.
    Can be 'auto', True, False, or a number of Fourier terms to generate.
holidays: pd.DataFrame with columns holiday (string) and ds (date type)
    and optionally columns lower_window and upper_window which specify a
    range of days around the date to be included as holidays.
    lower_window=-2 will include 2 days prior to the date as holidays. Also
    optionally can have a column prior_scale specifying the prior scale for
    that holiday.
seasonality_mode: 'additive' (default) or 'multiplicative'.
seasonality_prior_scale: Parameter modulating the strength of the
    seasonality model. Larger values allow the model to fit larger seasonal
    fluctuations, smaller values dampen the seasonality. Can be specified
    for individual seasonalities using add_seasonality.
holidays_prior_scale: Parameter modulating the strength of the holiday
    components model, unless overridden in the holidays input.
holidays_mode: 'additive' or 'multiplicative'. Defaults to seasonality_mode.

• • 參數擬合相關

growth: String 'linear', 'logistic' or 'flat' to specify a linear, logistic or
    flat trend.
changepoints: List of dates at which to include potential changepoints. If
    not specified, potential changepoints are selected automatically.
n_changepoints: Number of potential changepoints to include. Not used
    if input `changepoints` is supplied. If `changepoints` is not supplied,
    then n_changepoints potential changepoints are selected uniformly from
    the first `changepoint_range` proportion of the history.
changepoint_range: Proportion of history in which trend changepoints will
    be estimated. Defaults to 0.8 for the first 80%. Not used if
    `changepoints` is specified.

• • 不確定性相關

mcmc_samples: Integer, if greater than 0, will do full Bayesian inference
    with the specified number of MCMC samples. If 0, will do MAP
    estimation.
interval_width: Float, width of the uncertainty intervals provided
    for the forecast. If mcmc_samples=0, this will be only the uncertainty
    in the trend using the MAP estimate of the extrapolated generative
    model. If mcmc.samples>0, this will be integrated over all model
    parameters, which will include uncertainty in seasonality.
uncertainty_samples: Number of simulated draws used to estimate
    uncertainty intervals. Settings this value to 0 or False will disable
    uncertainty estimation and speed up the calculation.
stan_backend: str as defined in StanBackendEnum default: None - will try to

訓練過程

數據預處理

• 數據檢查

python.Prophet.forecaster.Prophet.setup_dataframe

Prophet會檢查模型輸入參數、數據的合法性，幫助使用者快速定位問題。比如：

• • 檢查輸入數據中是否有y列，ds列是否符合時間輸入規範，是否有缺失值。
  • 檢查添加的額外迴歸項，是否有缺失值，是否輸入數據中有添加的迴歸項數據。
  • 季節性項的condition列值是否是bool值等，用於控制模型選擇性的學習condition為True的樣本。
• 數據歸一化

python.Prophet.forecaster.Prophet.initialize_scales

對於y，有Absmax和Minmax兩種方式：現實場景中特徵值或y，往往有很大的量綱差異，會降低模型的性能、預測的準確性。Prophet內置了對y和對外部迴歸因子add regressors的歸一化。

• • AbsMax歸一化：
  • 含義：AbsMax歸一化是將原始數據縮放到[-1, 1]的範圍內，使數據的絕對值最大值為1。
  • 適用場景：AbsMax歸一化適用於數據中存在明顯的異常值或極端值的情況，可以保留數據的分佈形狀並減少異常值對模型的影響。
  • MinMax歸一化：
  • 含義：MinMax歸一化是將原始數據縮放到[0, 1]的範圍內，使數據的最小值對應0，最大值對應1。
  • 適用場景：MinMax歸一化適用於需要將數據映射到一個固定範圍內的情況，保留了原始數據的相對關係，在大部分機器學習算法中經常用到。

if self.scaling == "absmax":
    self.y_min = 0.
    self.y_scale = float((df['y']).abs().max())
elif self.scaling == "minmax":
    self.y_min = df['y'].min()
    self.y_scale =  float(df['y'].max() - self.y_min)
    ...
    ...

對於add regressor特徵則進行標準化，將特徵數據縮放到均值為0，標準差為1的標準正態分佈。

python/Prophet/forecaster.py:389

計算得到的y_scale和迴歸項的均值和標準差，會更新到Prophet類中，供預測階段使用。

自動設置週期性

python.Prophet.forecaster.Prophet.set_auto_seasonalities

如果在初始化Prophet類時，沒有指定季節性相關的參數，則會根據數據長度和間隔自動增加季節性項，三種不同的週期性默認的傅立葉階數為10。

當歷史數據大於等於兩年，則增加yearly seasonality，默認週期為365.25；
當歷史數據大於等於兩週，且相鄰兩數據之間的時間之差小於1周，則打開weekly seasonality，默認週期為7；
當歷史數據大於等於2天，且相鄰兩數據之間的時間小於1天，則打開daily seasonality，默認週期為1；

生成特徵寬表

Prophet模型的成分中劃分了seasonality features、holiday features和add regressors，但其實是一樣的處理方法。根據Prophet類初始化時的參數，生成特徵寬表，行為依次遞增的時間序列，列為每一個feature對應的值。

對於某一個seasonality特徵，根據傳入的週期性和傅立葉階數，生成不同列，列數等於傅立葉階數，列值等於某一階的週期性函數值。然後結合該特徵對應的condition_name的值，得到最終的特徵值。condition_name是True、False的np.array類型，用來指導模型學習condition_name列中為True的時間段數據，忽略為False的時間段的數據。

對於holiday features和add regressors，則對於每一個特徵，生成一列，列為每一個feature對應的值。特徵寬表的特徵總數為seasonality特徵的傅立葉階數+holiday features數+add regressors數。

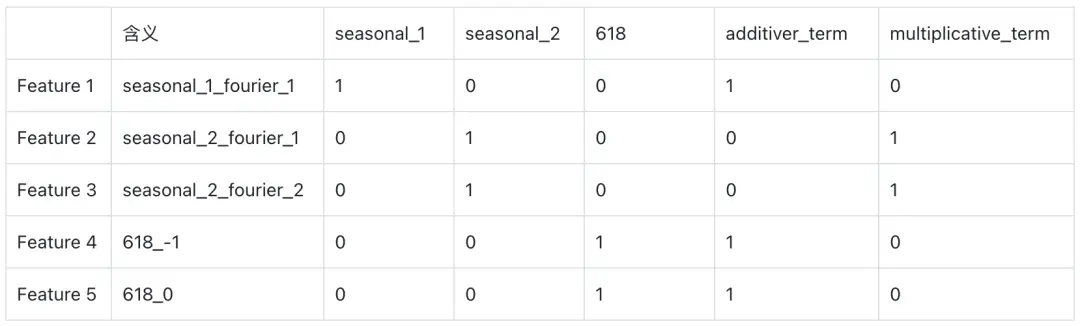
在生成特徵寬表的同時，Prophet會定義component_cols變量，來維護哪些列同屬於同一個成分。比如把同一個季節性項的多個周期函數合併成一個成分，把同一個節假日不同時間的因子合併成一個成分，把加性或者乘性因子項合併成一個成分，這樣可以方便進行模型的成分分析和結果可視化。比如給定一個Prophet模型：

m = Prophet(
holidays=pd.DataFrame({
  'holiday': '618',
  'ds': pd.to_datetime(['2021-06-18', '2022-06-18', '2023-06-18', '2024-06-18']),
  'lower_window': -1,
  'upper_window': 0,
  'mode': 'additive'
})) 


model.add_seasonality({'name':'seasonal_1','period':7, 'fourier_order':1,'mode': 'additive'})
model.add_seasonality({'name':'seasonal_2','period':365, 'fourier_order':2,'mode': 'multiplicative'})

假設yearly傅立葉階數為1的additive，weekly階數為2的additive函數，那麼component_cols為：

設置間斷點

python.Prophet.forecaster.Prophet.set_changepoints

首先當有人工設置間斷點時，以設置的間斷點為主，間斷點必須在訓練數據之內，否則會報錯。

當沒有設置間斷點時，Prophet會根據初始化的參數n_changepoints間斷點數和changepoint_range間斷點篩選範圍，進行自動採樣。例如時間序列有100個點，n_changepoints=10，changepoint_range=0.8，那麼Prophet會在前80個點中，等間隔的採樣10個點，作為候選間斷點。設置的間斷點數量不能超過changepoint_range範圍內的訓練集數量。

初始化stan參數

python.Prophet.forecaster.Prophet.calculate_initial_params

使用貝葉斯估計參數，需要給定參數的初始值，然後迭代至算法收斂，Prophet用全部訓練數據計算初始參數。每一項成分都需要進行參數初始化。

以線性趨勢為例，用標準化的y計算線性函數的斜率和偏置。其他迴歸項因子β，突變點增長係數δ都設置為0。

參數擬合

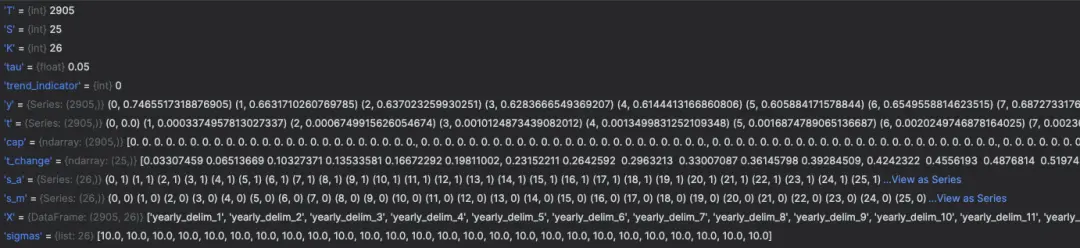
在初始化階段得到的參數和數據，轉化成字典形式傳入Stan進行參數擬合，字典格式如下所示：

字典K-V值和Prophet/stan目錄下的Prophet.stan腳本相對應，然後通過Pystan調用Stan引擎求解參數，擬合後的參數存儲在Propeht.params中，求解參數有兩種方式：

• 牛頓法/LBFGS法進行最大後驗估計

python.Prophet.models.CmdStanPyBackend.fit

• 馬爾可夫鏈蒙特卡羅法算法進行參數估計

python.Prophet.models.CmdStanPyBackend.sampling

預測過程

構建預測dataframe

python.Prophet.forecaster.Prophet.make_future_dataframe

我們可以通過Prophet類中的make_future_dataframe函數構建未來預測的DataFrame，預測長度、預測頻率由初始化參數periods、freq設置。

構建預測的DataFrame之後，和在訓練過程一致，需經過數據檢查、歸一化，歸一化使用訓練過程中計算得到的y_scale和迴歸項的均值和標準差。

點預測

點預測也就是在時間點上輸出單個預測值，預測值由趨勢預測和迴歸項預測組成。

• 趨勢預測

python.Prophet.forecaster.Prophet.predict_trend

在貝葉斯迴歸中，未知參數服從一個指定的先驗分佈，Prophet使用Stan引擎計算得到的返回參數的期望作為趨勢項公式的帶入值。

def predict_trend(self, df):
    k = np.nanmean(self.params['k'])
    m = np.nanmean(self.params['m'])
    deltas = np.nanmean(self.params['delta'], axis=0)


    t = np.array(df['t'])
    if self.growth == 'linear':
        trend = self.piecewise_linear(t, deltas, k, m, self.changepoints_t)
    elif self.growth == 'logistic':
        cap = df['cap_scaled']
        trend = self.piecewise_logistic(
            t, cap, deltas, k, m, self.changepoints_t)
    elif self.growth == 'flat':
        # constant trend
        trend = self.flat_trend(t, m)


    return trend * self.y_scale + df['floor']

對於flat、linear、logistic不同的趨勢分量，結合changepoints_t進行趨勢的預測，以線性趨勢為例。

python.Prophet.forecaster.Prophet.piecewise_linear

即論文中描述的公式：

最後根據訓練過程計算的y_scale縮放變量還原量級，作為最終的趨勢預測。

• 迴歸項預測

python.Prophet.forecaster.Prophet.predict_seasonal_components

上文提到的Prophet的seasonality features、holiday features和add regressors項，在參數求解過程中是一樣處理方法。

β即為擬合出的權重係數，β乘以特徵寬表對應的值，得到每個特徵的效應值。根據component_cols維護的不同成分的特徵歸屬。就可以得到seasonality、holiday features、add regressors、multiplicative_terms、additive_terms各個部分的效應值。這些在模型解釋性、結果可視化、偏差分析中都可以應用。

• 預測彙總

python/Prophet/forecaster.py:1287

預測成分彙總步驟把趨勢、季節性、節假日等預測效應值進行拼接，最後的預測結果公式如下：

預測結果值=趨勢*(1+乘法因素)+加法因素

預測的不確定性

Prophet通過觀測噪聲、參數不確定性以及未來趨勢不確定性三個部分輸出預測值的不確定性，最終通過yhat_lower、yhat_upper體現。

• 觀測噪聲不確定性

python/Prophet/forecaster.py:1556

一般時間序列分解模型，最後的一個分解項就是噪聲，Prophet也是這樣的，假設了輸入數據點含有服從正態分佈的觀測噪聲，Stan模型腳本中的sigma_obs就是擬合了這部分噪聲。觀測噪聲不確定性為：

sigma = self.params['sigma_obs'][iteration]
noise_terms = np.random.normal(0, sigma, trends.shape) * self.y_scale

變量sigma是sigma_obs的估計值。在每個時間步驟上，從正態分佈中採樣n_samples次，得到噪聲不確定項目noise_terms。

• 趨勢不確定性

python.Prophet.forecaster.Prophet._make_trend_shift_matrix

對於趨勢的不確定性，官方文檔中解釋：預測中最大的不確定性來源在於未來趨勢變化的可能性。因此我們盡最大可能採取了一個合理的假設，假設未來的趨勢變化會與歷史上觀察到的相似。特別是，我們假設未來的趨勢變化的平均頻率和幅度將與歷史上觀察到的相同。我們將這些趨勢變化進行投影，並通過計算它們的分佈來獲得不確定性區間。

具體而言，趨勢不確性由突變點出現的位置和突變的比例確定。首先計算曆史上突變點出現的間隔的均值*歷史上突變點的個數，得到每個時間點上產生突變點概率likelihood。然後計算曆史突變點的變化率的絕對值的均值mean_delta。最後進行採樣來模擬不確定性。均勻分佈採樣輸出矩陣（n_samples, future_length），對每一個元素判斷是否小於似然值likelihood，來判斷是否發生了突變，如果小於則發生了突變，然後輸出均值為mean_delta的拉普拉斯分佈，得到突變點變化率的採樣值。

• 參數的不確定性

python.Prophet.forecaster.Prophet.predict_uncertainty

當初始化參數MCMC=0，即調用Stan用MAP算法，此時算法得出的是收斂時的最終估計值，不確定性由觀測不確定性和趨勢不確定性組成，參數沒有不確定性的估計。

MCMC>0時候，除了觀測噪聲、趨勢不確定性外，由於Stan採用MCMC採樣方法，得到的返回值是待估計參數值的若干個採樣點，根據每個參數的採樣點得到不同的預測值。

• 不確定性結果輸出

進一步，由於每一個時間步有以上不確定性成分的n_samples個採樣數據。根據預設的置信度寬度，得到上、下分位數值：

lower_p = 100 * (1.0 - self.interval_width) / 2
upper_p = 100 * (1.0 + self.interval_width) / 2

對於每個時間步驟，求lower_p分位數、upper_p分位數，即得到yhat_lower、yhat_upper。

四、總結

Prophet框架在有明顯規律的單變量時序預測場景中有着非常不錯的表現。在得物的多個業務場景中已經得到了驗證。閲讀源碼能夠幫助我們更好的瞭解模型細節，在模型優化時幫助我們有的放矢，在模型選型時幫助我們掌握模型的適應性和侷限性。

參考資料

https://peerj.com/preprints/3190/

https://github.com/facebook/prophet

https://zhuanlan.zhihu.com/p/37543542

*文/ 探流

本文屬得物技術原創，更多精彩文章請看：得物技術

未經得物技術許可嚴禁轉載，否則依法追究法律責任！