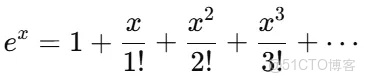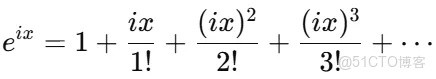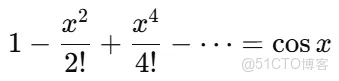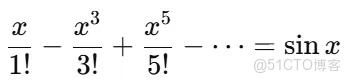(目錄)

一、複數

1. $Z^2=-1 \Rightarrow Z=\pm\sqrt{-1}=\pm i$

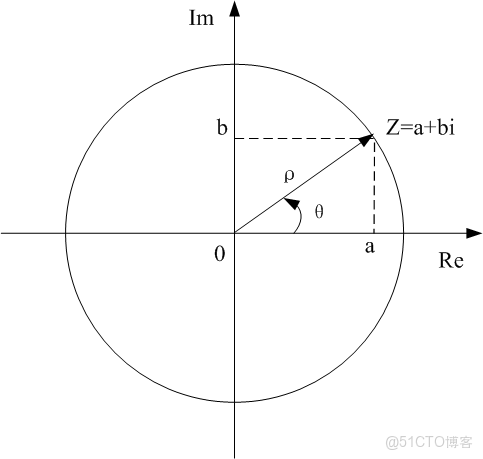
2. 複數的座標表示：$Z=a+bi$

3. 複數的三角表示：$Z=\rho(cos\theta+isin\theta)$

4. 乘法：棣莫佛定理 摸相乘，角相加。 $$ Z_1Z_2=\rho_1(cos\theta_1+isin\theta_1)\rho_2(cos\theta_2+isin\theta_2) \ =\rho_1\rho_2[(cos\theta_1cos\theta_2-sin\theta_1sin\theta_2)+i(sin\theta_1cos\theta_2+cos\theta_1sin\theta_2)] \ =\rho_1\rho_2[cos(\theta_1+\theta_2)+isin(\theta_1+\theta_2)] $$

5. 特別地 $i=cos\frac{\pi}{2}+isin\frac{\pi}{2} \Rightarrow Z \cdot i=\rho[cos(\theta+\frac{\pi}{2})+isin(\theta+\frac{\pi}{2})]$

二、數學中的五大常數齊聚一堂

在浩瀚的數學世界中，有一條公式常被譽為“上帝寫下的公式”，被數學家、物理學家乃至哲學家視為數學與宇宙間最優雅的橋樑。這條公式便是由18世紀瑞士數學家萊昂哈德·歐拉（Leonhard Euler）提出的： $$ e^{i\pi}+1=0 $$ 它簡單、緊湊，卻藴含着深刻的數學哲理。這條等式被稱為“歐拉公式”或“歐拉恆等式”，不僅連接了數學中五個最重要的常數，還將不同領域的數學理論串聯起來，展示了數學內部的和諧美。那麼，歐拉公式到底意味着什麼？它為什麼如此重要？

歐拉公式之所以令人驚豔，一個重要原因是它將以下五個數學常數以一種簡潔的方式組合在了一起： e：自然對數的底數，約等於2.718，是自然增長過程的核心。 i：虛數單位，滿足i2 =−1，是複數世界的入口。 π：圓周率，約等於3.14159，是圓和角度的代名詞。 1：乘法的恆等元素，是最基本的數字之一。 0：加法的恆等元素，是數學中“無”的概念象徵。

這五個數，原本屬於完全不同的領域：e來源於分析學、i源於複數、π來源於幾何，而0和1則屬於算術的最基本單位。但它們卻在歐拉公式中奇蹟般地組合在一起，形成了一個完美的等式。這種組合，既不是人為拼湊，也不是偶然巧合，而是深刻數學規律的體現。那麼，歐拉公式又是怎麼推導得來的呢？

三、歐拉公式的推導：從泰勒展開説起

歐拉公式的本質，其實是指數函數在複數領域中的自然擴展。為了理解它，我們可以從函數的泰勒展開式出發。泰勒展開是數學中一種用多項式近似函數的方法，形式如下：

當把x替換成虛數ix時，我們得到：

對其進行展開和整理，可以分為實部和虛部： 實部是：

虛部是：

於是我們得到： $$ e^{ix}=cosx+isinx $$

這便是歐拉公式的原始形式。特別地，當$x=\pi$時： $$ e^{i\pi}=cos\pi + isin\pi=-1+0i $$

因此： $$ e^{i\pi}+1=0 $$

也寫作$e^{i\pi}=-1$

四、從復指數，到旋轉的幾何意義

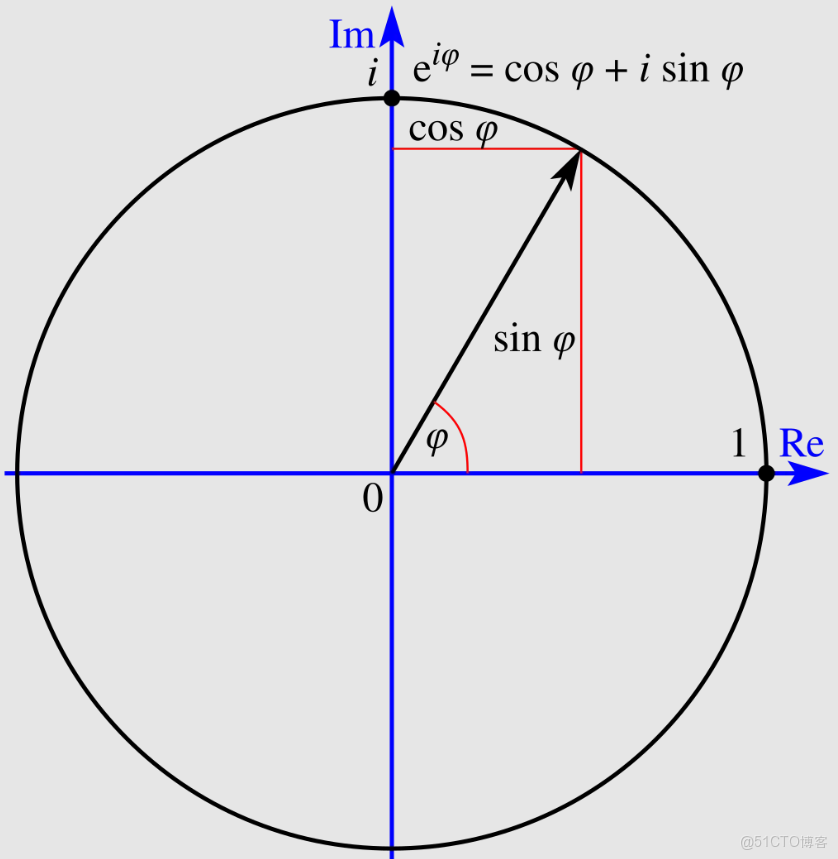
歐拉公式並不僅僅是一個抽象的數學等式，它在幾何中也有着生動而直觀的解釋。複數可以被看作是二維平面上的點或向量，而復指數$e^{i\theta}$則可以理解為單位圓上一點的位置，它與正實軸之間的夾角正好是$\theta$。換句話説，當我們把一個複數與$e^{i\theta}$相乘時，相當於將它在複平面上旋轉$\theta$弧度。

這意味着，復指數函數在複平面中承擔着“旋轉”的幾何作用。歐拉公式的幾何含義正是如此優雅：它將指數函數這種看似與方向無關的增長方式，與圓周運動這種週期行為緊密地連接起來。數學家們發現，這種聯繫不僅僅是一個巧妙的數學構造，更是自然界中許多現象的基礎。

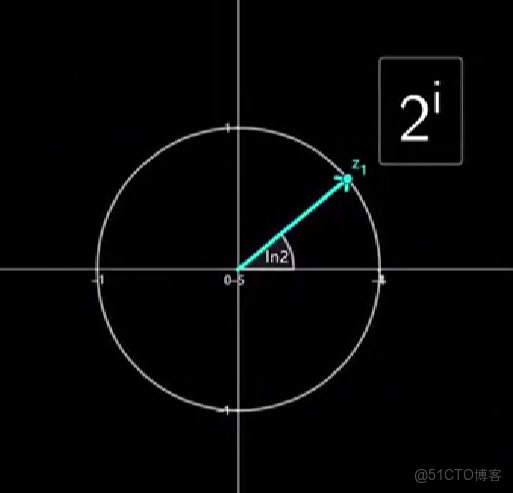
$2^i=(e^{ln2})^i=e^{iln2}$

五、複數函數的求解

歐拉公式：$\boxed{e^{i\theta}=cos\theta+isin\theta}$

1. $e^{a+bi}=e^ae^{bi}=e^a(cosb+isinb)$ $x^{a+bi}=(e^{lnx})^{a+bi}=e^{alnx+bilnx}$
2. $ln(a+bi)=ln(\rho e^{i\theta})=ln\rho+i\theta$
3. 聯立方程組 $$ \begin{cases} e^{i\theta}=cos\theta+isin\theta \ e^{-i\theta}=cos\theta-isin\theta \end{cases} \Rightarrow \begin{cases} sin\theta=\frac{1}{2i}(e^{i\theta}-e^{-i\theta}) \ cos\theta=\frac{1}{2}(e^{i\theta}+e^{-i\theta}) \end{cases} $$

六、歐拉公式的幾何推導

$ \lim_{n\rightarrow\infty}(cos\frac{\theta}{n}+isin\frac{\theta}{n})^n \ = \lim_{n\rightarrow\infty}(1+isin\frac{\theta}{n})^n $ 而 $ \lim_{n\rightarrow0}\frac{sinx}{x}=1 $ 原式子為 $ \lim_{n\rightarrow\infty}(1+\frac{i\theta}{n})^n $ 而 $ e=\lim_{n\rightarrow\infty}(1+\frac{1}{n})^n $

$e^r=\lim_{n\rightarrow\infty}(1+\frac{r}{n})^n$

令$\theta=\frac{n}{ik}$ 則原式為 $ \lim_{n\rightarrow\infty}(1+\frac{1}{k})^{ik\theta}=\lim_{n\rightarrow\infty}[(1+\frac{1}{k})^{k}]^{i\theta}=e^{i\theta} $