Let's be better ourselves together.
種一棵樹最好的時間是十年前,其次是現在。
如何用簡單遞歸實現指數型枚舉,組合型枚舉以及排列行枚舉?
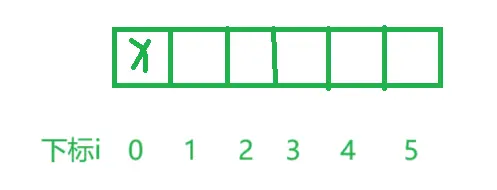
思路:我們可以把這一類題目想象成,有n個排列在一起的一列格子,我們需要按一定順序來填這些格子。
以下為三道HZOJ的題目作為例子。
235. 遞歸實現指數型枚舉
題目描述
從 1−n 這 n 個整數中隨機選取任意多個,每種方案裏的數從小到大排列,按字典序輸出所有可能的選擇方案。
輸入
輸入一個整數 n。(1≤n≤10)
輸出
每行一組方案,每組方案中兩個數之間用空格分隔。
注意每行最後一個數後沒有空格。
樣例輸入
3樣例輸出
1
1 2
1 2 3
1 3
2
2 3
3樣例輸入2
4樣例輸出2
1
1 2
1 2 3
1 2 3 4
1 2 4
1 3
1 3 4
1 4
2
2 3
2 3 4
2 4
3
3 4
4數據規模與約定
時間限制:1 s
內存限制:256 M
100% 的數據保證 1≤n≤10
思路: 從下標為0的格子開始,依次填數,在第i個位置可以選擇的最小數字是x的情況下,實現所有指數型枚舉。當i > 0,也就是已經選擇了至少一個數,輸出一種結果。
#include <iostream>
using namespace std;
int n;
int a[20];
//在第i個位置,最小為x
void f(int x, int i) {
if(i > 0) { //如果已經選擇了至少一個數字
for(int j = 0;j < i;j ++) {
if(j > 0) cout<<" ";
cout<<a[j];
}
cout<<endl;
}
for(int k = x;k <= n;k ++)
{
a[i] = k;
f(k + 1, i +1);
}
return ;
}
int main()
{
cin>>n;
f(1, 0);
return 0;
}236. 遞歸實現組合型枚舉
題目描述
從 1−n 這 n 個整數中隨機選取 m 個,每種方案裏的數從小到大排列,按字典序輸出所有可能的選擇方案。
輸入
輸入兩個整數 n,m。(1≤m≤n≤10)
輸出
每行一組方案,每組方案中兩個數之間用空格分隔。
注意每行最後一個數後沒有空格。
樣例輸入
3 2樣例輸出
1 2
1 3
2 3樣例輸入2
5 3樣例輸出2
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5數據規模與約定
時間限制:1 s
內存限制:256 M
100% 的數據保證 1≤m≤n≤10
思路:這道題和上一道題十分類似。從下標為0的格子開始,依次填數,在第i個位置可以選擇的最小數字是x的情況下,實現所有組合枚舉。不同的是邊界條件,上一道題當i > 0時即可輸出一種結果,這道題要填滿m個格子再輸出一種結果,所以邊界條件為i >= m。
#include <iostream>
using namespace std;
int n, m;
int a[20];
void f(int x, int i) {
if(i >= m) {
for(int j = 0;j < m;j ++){
if(j) cout<<' ';
cout<<a[j];
}
cout<<endl;
return ;
}
for(int k = x;k <= n;k ++) {
a[i] = k;
f(k + 1, i + 1);
}
}
int main()
{
cin>>n>>m;
f(1, 0);
return 0;
}237. 遞歸實現排列型枚舉
題目描述
從 1−n 這 n 個整數排成一排並打亂次序,按字典序輸出所有可能的選擇方案。
輸入
輸入一個整數 n。(1≤n≤8)
輸出
每行一組方案,每組方案中兩個數之間用空格分隔。
注意每行最後一個數後沒有空格。
樣例輸入
3樣例輸出
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1數據規模與約定
時間限制:1 s
內存限制:256 M
100% 的數據保證 1≤n≤8
思路:這道題其實就是輸出n的全排列。這道題需要注意的是,如何判斷當前的枚舉的這個數字是否出現過。所以我們需要使用一個bool數組來記錄它是否出現過。填數字的時候,先判斷是否出現,如果沒有出現(!st[k]),則填入數字。邊界條件是,當n個格子都填滿了, i == n,即完成了一種可能的排列。
#include <iostream>
using namespace std;
int n;
int a[10];
bool st[10];
void f(int i){
if(i == n) {
for(int j = 0;j < n;j ++) {
if(j > 0) cout<<' ';
cout<<a[j];
}
cout<<endl;
return ;
}
for(int k = 1;k <= n;k ++) {
if(!st[k]) {
a[i] = k;
st[k] = true;
f(i + 1);
st[k] = false;
}
}
}
int main()
{
cin>>n;
f(0);
return 0;
}