基於格的抗量子密碼

Introduction to the lattice-based quantum-resistant cryptography

抗量子密碼的安全性通常歸約到下面幾類數學難題的複雜度上：

基於格(lattice)的的最短向量問題(Shortest Vector Problem)和最近向量問題(Closest Vector Problem)
多元多項方程組求解問題
糾錯碼難題(error correction code problem)

其中基於格的抗量子密碼因為更易於實現而更受關注。

主要參考文獻：

[1]. Ajtai M. Generating hard instances of lattice problems[C]//Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. 1996: 99-108.

[2]. Micciancio D, Peikert C. Hardness of SIS and LWE with small parameters[C]//Annual cryptology conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 21-39.

[3]. Micciancio D, Peikert C. Trapdoors for lattices: Simpler, tighter, faster, smaller[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 700-718.

Peikert Chris的講座：Chris Peikert: Lattice-Based Cryptography

南方佛羅里達州大學格密碼導論課程：Lattice Based Cryptography

本文檔旨在提供基於格的抗量子密碼的入門介紹，主要闡述這些密碼原語是如何運行的，而不會涉及相關的數學以及複雜度證明

Algebra recap

回顧一些數學基礎知識(optional)，更多是回顧類似的數學思維。

ref. 1: 南方佛羅里達州大學-格密碼導論: lecture 1

ref. 2: 陳恭亮,《信息安全數學基礎》[M], 清華大學出版社, 2014.

域(Field)

Def.: 如果一個集合$K$對兩種二元運算封閉，即$K\times K \to K$，這兩種運算分別記作加法運算(+)和乘法運算($\cdot$)，並且集合$K$對加法構成交換羣，集合$K/\{0\}$對乘法構成交換羣，並且滿足分配律，那麼稱這個集合$K$以及該集合上的加法和乘法運算構成一個域。

$\mathrm{Remark}$: 比如實數集$\R$以及實數加法和乘法構成一個域，而整數集$\Z$上的加法和乘法不構成一個域，因為整數集合上的加法雖然構成交換羣，但是對於整數乘法運算卻不存在逆元。然而整數集$\Z_q$，$q$為素數，上的模運算構成一個有限域，比如在$\Z_7$中，$3\times 5\equiv1\mod 7$

因為交換羣需要在代數系（運算封閉的集合）的基礎上滿足結合律、單位元、逆元以及交換律，即：

$\forall a,b,c \in G, (ab)c = a(bc) \in G$

$\exist e\in G, ae=ea=a$

$\forall a\in G, \exist a^{-1}, aa^{-1}=a^{-1} a = e$

$\forall a,b\in G, ab=ba\in G$

環(Ring)

Def.: 如果一個集合$R$對兩種二元運算（分別記為加法和乘法）封閉，並且滿足以下條件：

$R$對加法構成交換羣
$R$上乘法運算滿足結合律，即$\forall a,b,c\in R, (ab)c=a(bc)$
同時加法和乘法滿足分配律，即$\forall a,b,c\in R,(a+b)c=ac+bc$

則稱$R$構成一個環。

$\mathrm{Remark} 1$ : 比如整數集合$\Z$就能構成一個環

如果環$R$上的乘法運算滿足交換律，即$\forall a,b\in R,ab=ba$，則稱環$R$為交換環

如果環$R$上的乘法存在單位元，即$\exist 1_{R}\in R, \forall a\in R,a1_R=1_Ra=a$，則稱環$R$為有單位元環或含幺環

如果環$R$上的乘法存在零因子，即$\exists a,b\in R, a\ne 0, b\ne 0, ab=0$，則稱環$R$有零因子

如果環$R$同時構成交換環以及含幺環，並且不存在零因子，則稱環$R$為整環

$\mathrm{Remark} 2$: 如果一個整環$R$，滿足$\forall a\in R, \exist a^{-1}\in R, aa^{-1}=1_R$，那麼這個整環就構成了一個域(Field)。

多項式環(Polynomial Ring)

Def.: 設$R$是整環，$x$是一個變量，則$R$上形如：$a_nx^n+\cdots +a_1x+a_0,a_i\in R$，的元素稱為$R$上的多項式，記多項式$f(x)=a_nx^n+\cdots +a_1x+a_0$的次數為$n$，記為$\deg f =n$

Thm.: 如果$R$構成整環，則其環上的所有多項式也構成也整環，記為$R[x]$，多項式環$R[x]$的加法和乘法運算為傳統的多項式加法和乘法，多項式環$R[x]$的加法單位元和乘法單位元為整環$R$的加法單位元，即$0_R,1_R$。

多項式環可以類比整數集$\Z$，存在不可約多項式（類比素數）、多項式同餘運算（類比整數同餘）和多項式歐幾里得除法，具體可參考[ref. 2]。

向量空間(Vector Space)

Def.: 對於一個n維的向量空間$V$以及域$K$，定義加法運算為向量與向量的加法$+: V\times V\to V$，定義乘法運算為標量與向量的乘法$\cdot: K\times V\to V$，則：

加法運算滿足結合律和交換律: $\forall u, v, w \in V: u + (v + w) = (u + v) + w, u + v = V + u$
加法運算存在零元: $\exist 0\in V, s.t. \forall v \in V, v + 0 = v$
乘法運算滿足結合律: $\forall \lambda, \mu \in K, \forall v \in V, \lambda\cdot(\mu\cdot v) = (\lambda \mu)\cdot v$
乘法運算存在單位元：$\exist 1,s.t. \forall v\in V, v\cdot 1 = 1\cdot v = v$
加法分配律: $\forall \lambda \in K, \forall u, v\in V, \lambda\cdot(u + v) = \lambda\cdot u + \lambda \cdot v$
乘法分配律: $\forall \lambda,\mu \in K, \forall v \in V, (\lambda + \mu)\cdot v = \lambda\cdot v + \mu\cdot v$

這樣的向量空間記作$K$向量空間$V$(K-vector space V)，記作$V(K)$

lemma: 若n維向量空間$V$中存在一組向量$w\subset V$滿足以下性質：

$\forall \alpha, \beta \in w, \alpha + \beta \in w$

$\forall \alpha \in w, \forall k \in K, k\alpha \in w$

則稱$w$是向量空間$V$的子空間。

$\mathrm{Remark}$: 向量空間也稱為線性空間。

生成元(Span of set)

Def.: 令$V$為定義在域$K$上的向量空間，以及向量組$S=\{v_1, v_2, ...\}$，則定義$S$的生成空間為：

$\mathrm{Span}(S) = \{v = \lambda_1 v_1 + \lambda_2 v_2 + ... | \lambda_i \in K, v_i \in V \}$

$\mathrm{Expample}$: 令$K=\R, V=\R^3, S=\{v_1, v_2, v_3\}, v_1 =(1,0,0), v_2=(0,1,0), v_3=(0,0,1)$

$\mathrm{Span}(S) = \{ \lambda_1 v_1 + \lambda_2 v_2 + \lambda_3 v_3 | \lambda_i \in \R \} = \R^3$

這裏S為規範基(canonical base)，所以S的生成空間就是這組規範基所有的線性組合，而向量空間定義為$\R^3$，所以S的生成空間也是$\R^3$

向量空間的基(basis)

Def.: 向量空間$V$的基就是滿足$\mathrm{Span}(S) = V$的最小集合S

比如上面例子中的$S=\{(1,0,0), (0,1,0), (0,0,1)\}$就是向量空間$\R^3$的一組基，但是如果令$S' = \{(1,0,0), (0,1,0), (0,0,1), (1, 1, 0)\}$，那麼也滿足$\mathrm{Span}(S') = \R^3$，但是$S'$不是最小集合，所以不是基。

Lemma.: 若向量空間$V$中存在一組向量$\alpha_1, ... \alpha_s$，滿足下列性質：

$\alpha_1, ..., \alpha_s$線性無關
向量空間$V$中的任意向量都能由$\alpha_1, ..., \alpha_s$線性表示

則稱$\alpha_1, ..., \alpha_s$維向量空間$V$的一組基。

Def.: 向量空間$V(K)$基($v_1, v_2, ..., v_s$)中的向量數量稱為這個向量空間的維數，$\forall \beta \in V, \beta = x_1 v_1 + x_2 v_2 + ... +x_s v_s, x_i\in K$，那麼稱($x_1, ..., x_s$)為向量$\beta$的座標

Def.: 向量空間可以有不同的基，這些基可以通過過渡矩陣進行轉換

線性映射

Def.: 令$V, U$為定義在$K$上的向量空間，$f: V\to U$是線性映射，當且僅當

$\forall v_1, v_2\in V, \forall \lambda,\mu \in K, f(\lambda v_1 + \mu v_2) = \lambda f(v_1) + \mu f(v_2)$

$\mathrm{Example}$: $V=\R^2, W=\R, f(x_1, x_2) = x_1 + x_2$

$f(\lambda v_1 + \mu v_2) = f(\lambda(x_1, y_1) + \mu(x_2, y_2))=\lambda x_1 + \mu x_2 + \lambda y_1 + \mu y_2 = \lambda f(x_1, y_1) + \mu f(x_2, y_2)$

如果$V=W$，則稱$f$為線性轉換。

線性映射矩陣

假設現在有兩個定義在域$F$上的向量空間$V(F), U(F)$，分別有兩組不同的基$\alpha_1, ...\alpha_n$和$\beta_1, ..., \beta_s$，且存在在一個線性映射$f: V\to U$則：

$\forall v\in V$，可以由$V$的基線性表示，即$v=\sum_{i=1}^nx_i\alpha_i$，則$f(v) = \sum_{i=1}^{n}x_if(\alpha_i)$

而$f(\alpha_i)\in U$，所以$f(\alpha_i)$ 也可以用$U$的基線性表示：

\[\begin{matrix} f(\alpha_1) &= y_{1,1}\beta_1 + ... y_{1,s}\beta_s\\ ...\\ f(\alpha_n) &= y_{n,1}\beta_1 + ... y_{n,s}\beta_s \end{matrix} \]

因此線性映射$f: V\to U$可以直接使用矩陣進行表示：

\[(f(\alpha_1), ..., f(\alpha_n)) = (\beta_1, ... ,\beta_s)\left(\begin{matrix} y_{1,1} & y_{2,1} & ... & y_{n,1} \\ \vdots & \vdots & \ddots & \vdots\\ y_{1,s} & y_{2,s} & ... & y_{n,s} \end{matrix}\right) \]

稱上述矩陣為線性映射$f$在基偶$\{\alpha_i\}_1^n, \{\beta_i\}_i^s$下的矩陣表示。

$\star$: 已知映射$f:A\to B$，那麼可以通過$M_f=[f(e_1), f_(e_2),\dots, f(e_n)]$得到對應的矩陣滿足$f(A)\cong M_f(A)$

格論(Lattice Theory)

ref.: Micciancio, D., Regev, O. (2009). Lattice-based Cryptography. In: Bernstein, D.J., Buchmann, J., Dahmen, E. (eds) Post-Quantum Cryptography. Springer, Berlin, Heidelberg.

格的定義

格(Lattice)是一個由$n$維的點組成的集合，這些點呈現出週期性的規律，如下圖所示是一個二維格：

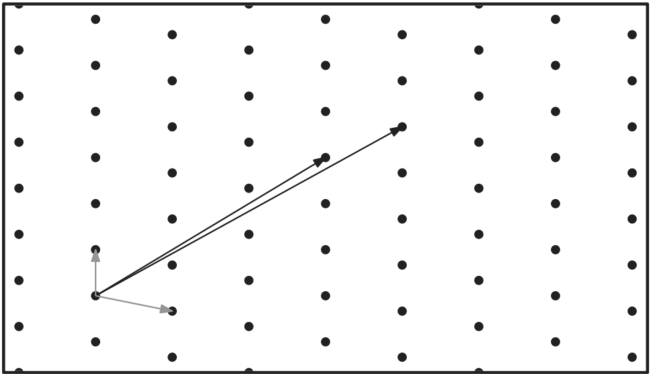
Def.: 給定$n$組線性無關的$m$維向量，$b_1,...,b_n\in \R^m$，則由這些向量生成的格定義為：

$\mathcal{L}(b_1, ..., b_n) = \{\sum_{i=1}^n x_ib_i, x_i\in \Z\}$

這裏將向量$b_1, ..., b_n$稱為格的基(basis)，基向量組中的向量數($n$)稱為格的秩(rank)，基向量的維數($m$)稱為格的維度(dimension)，如果格的秩等於格的維度，即$n=m$，則稱這個格是滿秩格(full-rank lattice)。

從生成方式來看，格和向量空間類似，都是一組線性無關的基向量通過線性組合形成，但是兩者的區別在於，向量空間的係數屬於域，通常是連續的，比如$\R$；而格的係數是整數$\Z$，通常是離散的。

Lemma1: 格的基也可以用矩陣進行表示，令基向量作為矩陣的列向量，即$B=(b_1, ..., b_n)\in \R^{m\times n}$，那麼這種情況下，格也可以定義為：$\mathcal{L}(B) = \{Bx, x\in \Z^n\}$，這裏的$Bx$就是傳統的矩陣-向量乘法。

Lemma2: 那麼也就不難發現如果矩陣$U$是幺模(unimodular)矩陣，即滿足$|B| = ±1$，那麼由矩陣$B$和矩陣$BU$生成的格將會是相同的，即：

$\mathcal{L}(B) = \mathcal{L}(B')\iff \exist U, s.t., |U| = ±1, B' = BU$

也就是説，同一個格可以有多個不同的基，這一性質將會在基於格的密碼學中多次出現。

Def.: 對於格$\mathcal{L}(B)\in \R^n$，格的行列式定義為矩陣基的行列式的絕對值，即：

$\det(\mathcal{L}(B)) = \sqrt{\det(B^TB)}$

特別的，當$\mathcal{L}$為滿秩格時，$\det(\mathcal{L}(B)) = |\det(B)|$

顯然，格的行列式不會因基的變換而發生變化。

格的行列式的幾何意義是格中單元格的體積，或者説其倒數就是格中點的密度。

Def.: 對於格$\mathcal{L}(B)\in \R^n$，$\mathcal{L}(B)$的對偶格定義為$\mathcal{L}(B)^* = \{<x,y>\in \Z, \forall y\in \R^n,\forall x\in\mathcal{L}\}$，可通過下面的方法得到格的對偶：

$\mathcal{L}(B)^*=\mathcal{L}((B^{-1})^T)$

顯然，$\det(\mathcal{L}^*) = 1/\det(\mathcal{L})$

q階格

前面所介紹的格都是定義在整數集合上的格，為了方便計算機計算，引入q（通常是素數）階格的概念。

Def.: 對於整數$q$，若格$\mathcal{L}$滿足$q\Z^n \subseteq \mathcal{L}\subseteq\Z^n$，則稱$\mathcal{L}$為一個q階格。

$\forall q\in\Z,s.t.\det(\mathcal{L}) | q$，則$\mathcal{L}$都是一個q階格。不過在基於格的密碼學中通常討論$q<\det(\mathcal{L})$的情況。

$q$階格的含義是，整數$q$與任何標準基向量的線性組合得到的向量都屬於這個格。或者説，將$q$階格中的任意一個點按照任意的方向平移$q$個單位，最終得到的點還是屬於這個$q$階格。

$q\Z^n$的含義是整數$q$與集合$\Z^n$中的向量數乘運算得到的集合。

Lemma: 給定矩陣$A\in \Z_q^{n\times m}$，則可以如下定義兩個不同的q階格：

$\Lambda_q(A) = \{y\in\Z^m, y\equiv A^Ts\mod q, s\in\Z^n \}$
$\Lambda_q^{\perp}(A)=\{y\in \Z^m, Ay\equiv 0\mod q \}$

$q$階格$\Lambda_q(A)$中的向量由矩陣$A$的行向量模$q$線性組合生成，而$q$階格$\Lambda_q^{\perp}(A)$則是由與矩陣$A$的行向量模$q$正交的向量生成。

令$A=(a_1, a_2, ..., a_n)^T, a_i\in\Z_q^m$，即$a_i\in\Z_q^m$是矩陣$A\in\Z_q^{n\times m}$的行向量，則

$\Lambda_q(A) = \mathcal{L}(a_1, a_2, ..., a_n)=\{\sum_{i=1}^n x_ia_i, x_i\in\Z^n\}$

$\Lambda^{\perp}_q(A)=\{y\in \Z_m: <y, a_i>\equiv 0\mod q,\forall a_i\in A\}$

並且這兩個q階格互為對偶，即$\Lambda_q^{\perp}(A) = q\cdot\Lambda_q(A)^*$，$\Lambda_q(A) = q\cdot \Lambda_q^{\perp}(A)^*$

格問題

基於格的計算性難題主要為：

最短向量問題(Shortest Vector Problem, SVP)：給定格$\mathcal{L}(B)$，找到這個格中最短非零的向量
最近向量問題(Closest Vector Problem, CVP)：給定格$\mathcal{L}(B)$，以及目標向量$t$，目標向量可能並不在格中，在格中找到點$v\in\mathcal{L}(B)$，點與目標向量$t$的距離最近
最短線性無關向量組問題(Shortest Independent Vectors Problem, SIVP)：給定格$\mathcal{L}(B), B\in\Z^{n\times n}$，找到$n$組線性無關的格向量$S=[s_1, ..., s_n], s_i\in\mathcal{L}(B)$，使$||S|| = max_i||s_i||$最短

這裏的向量長度是指歐幾里得範數：$||x||=\sqrt{\sum_i}x_i^2$

SVP難以求解的原因在於，格是離散的，格中的點或向量只能通過格的基線性表出。換句話説，給定一組隨機的基，找到這組基的某個線性組合，使其歐幾里得範數最小。

同時SVP的難度是可以控制的，以二維格舉例，選擇兩條內積儘可能小（長度短且近似於相互垂直）的向量作為基(good baisis)，就能更容易地算出最短非零向量；但是如果選擇兩條內積很大（長度長且近似於相互重合）的向量作為基(bad basis)，那麼就很難算出最短非零向量(ref. how to define a good basis and a bad basis?)。

正如前面提到的，格與向量空間的區別在於：格的係數屬於整數集，而向量空間的係數屬於域，所以這就導致最短非零向量問題在格中很難求解，而在向量空間中就不是一個問題：如果向量空間定義在無限域上，那麼最短向量的長度將無限逼近0，而不存在；如果向量空間定義在有限域上（通常構成一個環），那麼最短向量的長度就是1，即有限域的乘法單位元。

在格密碼中，通常會考慮這些問題的漸進變式，用$\gamma$作為下標表示這些問題的漸進因子。

比如$SVP_{\gamma}$的目標是找到某個向量，該向量的長度（或者説向量範數，norm）最多是真正最短向量的$\gamma$倍。

利用格論構造加密算法最早是由Ajtai(Generating hard instances of lattice problems. In Complexity of computations and proofs, volume 13 of Quad. Mat., pages 1–32. Dept. Math., Seconda Univ. Napoli, Caserta (2004). Preliminary version in STOC 1996.)提出的。

在q階隨機格中求解SVP

這裏討論(Optional)如何在q階隨機格中解決SVP。

一方面是為了展示SVP的複雜度。

另一方面，基於格的攻擊(lattice-based attack)方法的實現原理，就是將已有的數學難題（比如大整數分解問題）轉換成在q階隨機格中的SVP，然後求解以破解密碼算法。

給定隨機矩陣$A\in\Z_q^{n\times m}$，其中$m>n$，假設$q$為素數，現在要求在合理時間內從q階隨機格$\Lambda^{\perp}_q(A)$中找到一條短向量。

想要解決這樣的問題，首先需要估計格中最短非零向量的長度是多少。

假設$A$中的行向量都是線性無關的，那麼$\Z_q^m$中屬於$\Lambda_q^{\perp}(A)$的元素數量就是$q^{m-n}$，這種情況下$\det(\Lambda_q^{\perp}(A))=q^n$

即$q$階格$\Lambda_q^{\perp}(A),A\in\Z_q^{n\times m}$中單元格的最小體積為$q^n$

在n維球體(or hypersphere)的體積計算公式：$V = \frac{\pi^{n/2}}{(n/2)!}r^n$

比如二維球體就是圓，其體積就是面積即$\pi r^2$

三維球體就是立方球，其體積公式為$\frac{4}{3}\pi r^3$，注意，$(\frac{3}{2})!=\Gamma(\frac{3}{2} + 1) = \frac{3}{4}\sqrt{\pi}$

根據此公式可以推算出$q$階格$\Lambda_q^{\perp}(A), A\in \Z_q^{n\times m}$，其元素$v\in \Z^m$，中單位球體的最小半徑：

\[\begin{align} \frac{\pi^{m/2}}{(m/2)!}r^m&=q^n\\ r^m &= \frac{q^n\cdot (m/2)!}{\pi^{m/2}}\\ r &= \frac{q^{n/m}\cdot ((m/2)!)^{1/m}}{\sqrt{\pi}}\\ r &\approx q^{n/m}\cdot \sqrt{\frac{m}{2\pi e}} \end{align} \]

上述半徑通常記為$\lambda_1(\Lambda_q^{\perp}(A))$，即$\lambda_1(\Lambda_q^{\perp}(A)) \approx q^{n/m}\sqrt{\frac{m}{2\pi e}}$

當$m$取值越合理時，即$m$遠大於$n$，同時$m$取值也不是很大時，上述的估值越準確。

格規約方法

$\mathcal{Notion}$: 格規約(Lattice Reduction)，是指找到格的一組基，這組基的長度儘可能短並且幾乎是相互正交的。格規約算法就是解決SVP的一種方法。

這裏不討論具體的格規約算法，只是討論通過已知的格規約算法能夠找到的最短向量的長度是多少

根據Gama以及Nguyen等人的總結性研究(Predicting lattice reduction[C]. Advances in Cryptology–EUROCRYPT 2008)，通過已知的最優格規約算法在$m$維$q$階格$\Lambda_q^{\perp}(A)$中找到的短向量的長度接近於

$\min\{q, (\det(\Lambda_q^{\perp}(A)))^{1/m}\cdot \delta^m\} = \min\{q, q^{n/m}\cdot \delta^m\}$

其中參數$\delta$取決於所使用的格規約算法，參數$\delta$越大就説明格規約算法速度越快，參數$\delta$越小就説明格規約算法精度越高，這個參數取值通常接近於1，但不小於1.01。

如果令$f(m)=q^{n/m}\cdot\delta^m$，則當$m=\sqrt{n\log q/\log\delta}$時函數$f(m)$取最小值$2^{2\sqrt{n\log q\log\delta}}$，即，當$m$取更小的值，則會因為格變得稀疏而找不到足夠的短向量，當$m$取更大的值，則會因為格的高維度使格規約變得困難。

可以看到格規約能找到的短向量的長度與格的維度$m$是無關的。

組合方法

已知的一種通過組合方法(combinatorial method)求解q階隨機格SVP的算法在研究(Lyubashevsky, V., Micciancio, D., Peikert, C., and Rosen, A.: SWIFFT: a modest proposal for FFT hashing. In FSE 2008 (2008))中具體演示，在該研究中能夠通過此算法對基於格的哈希函數實現攻擊。

給定隨機矩陣$A\in\Z_q^{n\times m}$，可以通過下面的方法在格$\Lambda_q^{\perp}(A)$中找到座標限制在$[-b,b]$內的點：

將矩陣$A$的列向量分成$2^k$組，則每組包含$m/2^k$個列向量

![1](C:\Users\yangzihang\Pictures\Saved Pictures\combinatorial_1.png)
每組列向量進行線性組合：$\{y=c_ia_i,-b\ge c_i\ge b\}$，這樣每個向量組中就包含$(2b+1)^{m/2^k}$個列向量

![2](C:\Users\yangzihang\Pictures\Saved Pictures\combinatorial_2.png)
每兩個向量組$g_1, g_2$進行組合得到新的向量組$g': \{y=x_1+x_2,x_1\in g_1,x_2\in g_2\}$，其中向量$y$的前$\log_q{L}$個座標都為0，其中$L=(2b+1)^{m/2^k}$

考慮到前$\log_q{L}$個座標取值有$q^{\log_q{L}}=L$種可能性，所以合併後得到的向量組中包含大約$L\cdot L/L=L$個向量
這樣能夠得到$2^{k-1}$個向量組，每個向量組中包含$L$個向量，每個向量的前$\log_q{L}$個座標都為0
繼續進行上面的組合，直到第$k$輪迭代，只得到一個向量組，只包含$L$個向量，並且這些向量的前$k\cdot\log_q{L}$個座標都是0

其中參數$k$的選擇如下：$\frac{2^k}{k+1}\approx \frac{m\log{(2b+1)}}{n\log{q}}$

最後一個向量組中的向量通過矩陣$A$的列向量進行線性表示，這樣就能夠得到所需要的向量。

組合的方法總是能夠成功，但是其複雜度會隨着格的維度$m$的增大而增大。

如果想要讓基於格的密碼體系達到一定的安全程度，那麼可以使用基於組合的攻擊來確定所需的安全參數大小。

短整數解(SIS)

ref. 1: Ajtai M. Generating hard instances of lattice problems[C]//Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. 1996: 99-108.

ref. 2: Peikert Chris的講座

短整數解問題

短整數解(Short Integer Solution)問題最早由Ajtai(96's)提出，對格難題進行規約從而得到一個單向函數(One-way function)，這個難題進一步演化至如下定義：

Def.: 令$n,q\in\Z, \beta\gt 0$，其中$n$是主要的安全參數，而$q=\mathrm{poly}(n)$。給定均勻隨機的矩陣$A\in\Z_q^{n\times m}$，其中$m=\mathrm{poly}(n)$，要求找到一個非零整數向量$z\in\Z^m$，滿足$Az\equiv 0\mod q$，並且$||z|| \lt \beta$。

這個問題看上去是一個很自然的線性代數問題，但問題的難點在於，需要同時滿足等式以及係數長度的限制。

SIS問題的困難性證明(proof of hardness)是將短整數解問題歸約到格的SVP上。換句話説，如果算法$\mathcal{A}$能夠解決SIS問題，那麼$\mathcal{A}$也能解決格的SVP。然而SVP被認為是難以解決的，所以SIS問題也是難以解決的。

可以發現，在SIS問題中$\beta$的取值需要足夠大，否則SIS問題無解。但同時$\beta$取值如果太大，即$\beta\gt q$，那麼這個問題又會變得很容易。通常$\beta$的取值是$q\gt \beta\gt \sqrt{n\log{q}}$。

Thm.: Ajtai在文獻[ref. 1]中證明，如果參數選擇合理，那麼解決平均情況下SIS的困難程度至少是和解決最壞情況下$n$維格下SVP一樣的。

關於SIS問題如何求解，所涉及的資料較為複雜。簡單的理解是，既然SIS問題是歸約到SVP上的，而SVP問題在短且正交的基向量下容易求解。

如果能夠知道這樣的基向量，那麼也就能就求解SVP，進而求解SIS問題。

短整數解問題通常被用於構建單向函數(One-way Function)，也就是從一個方向計算會很容易，但是從另一個方向計算將會變得很難。

基於SIS哈希函數

令$m\gt n\log_qq$，定義函數$f_A:\{0,1\}^m\to\Z_q^n$

$f_A(x)\equiv Ax\mod q$

如上定義的函數具備抗碰撞性(collosion resistant)，即給定$x\in\{0,1\}^m$，以及$y=Ax\mod q$，難以計算出$x'\in\{0,1\}^m,x'\ne x$，滿足$Ax'\equiv y\mod q$

否則，如果能找到$x'\ne x$滿足，$Ax'\equiv Ax \mod q$，那麼就能找到$x''=x'-x\ne 0$，滿足$Ax''\equiv 0\mod q$

也就是SIS問題的解。

這個哈希函數的抗碰撞性依賴於SIS問題的複雜度，如果能夠找到某個碰撞對，那麼也能解決SIS問題。

基於SIS數字簽名

生成均勻隨機的矩陣$vk = A$作為公鑰，以及私鑰$sk=T$

簽名算法$\mathrm{Sign}(T,\mu)$: 對於消息$\mu$，以及哈希函數$H(\cdot)$，使用$T$作為參數在某個隨機分佈（通常是離散高斯分佈）中採樣得到$z\in\Z^m$，使得$Az=H(\mu)$，將$z$作為消息$\mu$的簽名

隨機採樣$z$不會泄露任何關於私鑰$T$的信息

驗籤算法$\mathrm{Verify}(A,\mu,z)$: 檢查是否滿足$Az=H(\mu)$

如果敵手想要偽造另一條消息$\mu'$的，則需找到簽名$z'\in\Z^m$，滿足$Az'=H(\mu')$，也就是需要解決SIS問題。

容錯學習(LWE)

ref. 1: 南方佛羅里達州大學-格密碼導論: lecture 2

ref. 2:https://courses.grainger.illinois.edu/cs598dk/fa2019/Files/lecture10.pdf

容錯學習問題

這裏先介紹以下非容錯學習(Learning Without Error)。

假設有$m$個向量$a_i\in \Z_q^n$，以及一組內積$b_1=< s,a_1>, ..., b_m=<s,a_m>$，如何找到$s\in \Z_q^n$

這個問題其實就是一個解方程組問題：

\[\begin{cases}\begin{align}a_{1,1}\cdot s_1 + a_{1,2}\cdot s_2 + ... + a_{1,n}\cdot s_n &= b_1\\ a_{2,1}\cdot s_1 + a_{2,2}\cdot s_2 + ... + a_{2,n}\cdot s_n &= b_2\\ ...&\\ a_{m,1}\cdot s_1 + a_{m,2}\cdot s_2 + ... + a_{m,n}\cdot s_n &= b_2\end{align}\end{cases} \]

能夠直接通過高斯消元法求解:

令

\[A = \left(\begin{matrix}a_{1,1} & ... & a_{1,n} \\ a_{2,1} &...& a_{2_n}\\\vdots&\ddots&\vdots&\\a_{m,1}&...&a_{m,n}\end{matrix}\right) \]

則$As = b$，得到增廣矩陣$(A|b)$，將其進行初等行變換得到$(E|s)$後得解。

$\mathrm{Example}: q = 3$，$A=\left(\begin{matrix} 2 & 2 & 0\\0 & 1 & 1\\ 0 & 2 & 0\end{matrix}\right)， b = \left(\begin{matrix}1\\1\\0\end{matrix}\right)$

則$(A|b) = \left(\begin{matrix} 2 & 2 & 0 & 1\\0 & 1 & 1 & 1\\ 0 & 2 & 0 & 0\end{matrix}\right)$，經過一系列初等行變換後可以得到：$(E|s) = \left(\begin{matrix} 1 & 0 & 0 & \frac{1}{2}\\0 & 1 & 0 & 0\\ 0 & 0 & 1 & 1\end{matrix}\right)$

得解$s = \left(\begin{matrix}\frac{1}{2}\\0\\1\end{matrix}\right)$

$\mathcal{Initution}$: 可以看到上面這個問題能夠通過高斯消元法輕易求解，而容錯學習(Learning With Error)就是在上面這個問題的基礎上，僅僅給出大約值，即$b_i\approx <a_i, s>$，這樣能夠讓上面這個問題難以求解。

具體方法就是引入一個誤差值：$b_i=<a_i,s> + e_i$

$\mathrm{Remark}$: 容錯學習問題的困難程度取決於所引入隨機誤差的分佈，而這些誤差分佈都被證明：從這些誤差分佈中所選取的誤差能夠讓容錯學習難以求解。

誤差分佈

Def.: 高斯分佈，其實也就是正太分佈：

$\mathcal{Proposition}: \int_{\R} e^{-x^2} dx = \sqrt{\pi}$

可由此得到概率密度函數：

$g_{\mu,\sigma}: x\to \frac{1}{\sigma \sqrt{2\pi}} e^{\frac{-(x-\mu)^2}{2\sigma^2}}$

其中$\mu$為概率分佈的平均值，$\sigma$為概率分佈的方差。

回顧概率論

概率密度函數：$\Pr[X\ge x] = F(x) = \int_{-\infin}^{x} f(x) dx$，其中$f(x)$為概率密度

$\Pr[X=x]\approx f(x)dx$

$\int_{-\infin}^{\infin} f(x)dx = 1$, $\int_{-\infin}^{\infin} xf(x)dx =\mu$, $\int_{-\infin}^{\infin} (x-\mu)^2 f(x)dx =\sigma ^2$

其中$\mu$為平均值，$\sigma^2$為方差

在容錯學習中，通常取高斯分佈的參數$\mu=0$，這樣能夠讓誤差值更有可能取到接近0的值（但不總是0）。

對概率分佈取整

上面所提到的誤差分佈通常是連續的，所以隨機變量的取值範圍落在實數集上，但現在需要讓隨機變量的取值落在整數集上，所以需要對其進行取整(round the distribution)。

對於一個隨機變量$X$，假設其概率密度函數為$f(x)$，則對該隨機變量取整得到的隨機變量$X_{\Z}=\lceil X\rfloor$

$\Pr(X_{\Z}=N) = \Pr(X\in (N-\frac{1}{2}, N+ \frac{1}{2}]) = \int_{N-\frac{1}{2}}^{N+\frac{1}{2}} f(x)dx$

對概率分佈取模

在得到取值落在整數集上的隨機分佈$X_{\Z}$後，進一步需要讓隨機變量的取值落在一個有限域上，所以需要對齊進行取模。

對於一個隨機變量$X$，假設其概率密度函數為$f(x)$，則對該隨機變量取模得到的隨機變量$X_{\Z_q} = X_{\Z}\mod q$

\[\begin{align} \Pr(X_{\Z_q} = [a]) &= \Pr(X_{\Z} = a + kq), k\in\Z \\ &= \sum_{k\in\Z} \Pr(X_{\Z} = a + kq) = \sum_{k\in\Z}\int_{a+kq-\frac{1}{2}}^{a+kq+\frac{1}{2}}f(x)dx \\ &= \int_{a-\frac{1}{2}}^{a+\frac{1}{2}}g(x)dx \end{align} \]

其中$g(x): x\to \sum_{k\in\Z}f(x+kq)$

LWE Problem

Thm. 1: 令$\mathcal{X}$為取整模$q$的高斯分佈，$e_i\leftarrow\mathcal{X}$，$m,n\gt 0\in \Z$，給定$m$組採樣數據：$a_i, <a_i,s> + e_i$，其中$a_i$在向量空間$\Z^n_q$中隨機均勻採集，則根據採樣數據計算出$s$是困難的。

如上定義的LWE問題是一種搜索(search-LWE)問題，在此基礎上還有一種決策(decision-LWE)問題，即給定隨機矩陣$A$以及如上定義的採樣數據$b$，以及另一組均勻隨機生成的矩陣和向量$A',b'$，是否能夠區別$(A,b)$以及$(A',b')$，決策問題同樣也是困難的。

Thm. 2: 平均情況下的LWE問題的複雜度比最壞情況下的SVP以及SIVP更難(Micciancio D, Peikert C. Hardness of SIS and LWE with small parameters[C]//Annual cryptology conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 21-39.)，即：

$SVP_{\gamma},SIVP\le search-LWE\le decision-LWE$

$\mathrm{Example}$: 給定採樣數據：

$14s_1 + 15s_2 + 5s_3 + 2s_4 \approx 8 \mod 17$

$13s_1 + 14s_2 + 14s_3 + 6s_4 \approx 16 \mod 17$

$6s_1 + 10s_2 + 13s_3 + 1s_4 \approx 3 \mod 17$

$\cdots$

而秘密值$s = (0, 13, 9, 11)$，將正確值代入後可以得到每個採樣數據的誤差。

在LWE問題中，誤差值$e_i$既不會公開，也不會作為秘密值保存。

基於LWE私鑰加密

利用LWE問題中的秘密信息$s$作為密鑰實現單比特信息的對稱加密。

參數選擇：$n > 0, q > 0, \mathcal{X}_{\sigma}$ 通過適當的參數$\sigma$ 令 $\Pr(|e_i|\le q/4)$ 儘可能高。

加密：對單比特信息$\mu\in\{0，1\}$，在$\Z_q^n$中均勻隨機地選擇向量$a$，$e\leftarrow \mathcal{X}_{\sigma}$，密鑰$s$，密文$c=(a, <a,s> + e + \mu\cdot\lfloor q/2\rfloor \mod q)=(a,b)$

解密：$b-<a,s>\mod q = e + \mu\cdot\lfloor q/2\rfloor\approx \mu\cdot\lfloor q/2\rfloor$

如果$\mu\cdot\lceil q/2\rfloor \le q/4$，則$\mu=0$
如果$\mu\cdot\lceil q/2\rfloor\ge q/4$，則$\mu=1$

這是$\mu$要麼是0要麼是1，所以($e + \mu\cdot\lceil q/2\rfloor$)的數值要麼是($e+0$)要麼是($e+\lceil q/2\rfloor$)，而其中$e$主要分佈在$[- q/4, q/4]$區間，所以該算法大概率能成功解密，但是當$|e|> q/4$時還是會失敗，這取決於高斯分佈$\sigma$的選擇。

此加密方案的安全性證明見[ref. 2]。

基於LWE公鑰加密

在LWE問題中，採樣數據具有線性運算的性質，即：

$(a_1, <a_1,s> + e_1) + (a_2, <a_2,s> + e_2) = (a_1 + a_2, <a_1 + a_2, s> + e_1 + e_2) = (a', <a',s> + e')$

其中$a' = a_1 + a_2, e'=e_1 + e_2$

根據這一性質可以基於LWE問題實現單比特的公鑰加密，將秘密信息作為私鑰，而將採樣數據作為公鑰。

參數選擇：$n > 0, q > 0$以及取整求模的高斯分佈$ \mathcal{X}$，私鑰：$s\in\Z^n_q$，公鑰，即採樣數據，$(a_1, b_1 = <s,a_1> + e_1), ..., ((a_k, b_k=<s, a_k>+ e_k))$，其中$a_i$在$Z_q^n$中隨機均勻選擇，$e_i\leftarrow \mathcal{X}$

加密：明文$\mu\leftarrow\{0,1\}，$密文$c=\sum_{i=1}^k b_k + \mu\cdot\lceil q/2\rfloor \mod q$

解密：計算$c - <s,\sum_{i=1}^k a_i> \mod q\approx \mu\cdot\lceil q/2\rfloor$

$\mu\cdot\lceil q/2\rfloor$接近0，則$\mu = 0$
$\mu\cdot\lceil q/2\rfloor$接近$\lceil q/2\rfloor$，則$\mu=1$

$\mathrm{Example}$:

LWE問題的採樣數據為：

\[\begin{align} 21 s_1 + 19 s_2 + 30 s_3+48 s_4 &\approx 39 \mod 89\\ 4 s_1 + 24 s_2 + 33 s_3 + 38 s_4 &\approx 20 \mod 89\\ 5 s_1 + 24 s_2 + 79 s_3 + 27 s_4 &\approx 49 \mod 89 \end{align} \]

將其加起來可以得到: $30s_1 + 67s_2 + 53s_3 + 24s_4 \approx 19\mod 89$，而這就是Bob的公鑰

而方程組真正的解$(10, 82, 50, 5)$則作為私鑰保存。

如果Alice想要加密1，則發送$c = 19 + 44 = 63$，Bob收到密文後，利用私鑰計算$63 - 30\times 10 + 67\times 82 + 53\times 50 + 24\times 5 = 43\mod 89$，這個值更加接近$\lceil q/2\rfloor $，因此明文為1

如果Alice想要加密0，則發送$c = 19$，Bob收到密文後，利用私鑰計算$19 - 30\times 10 + 67\times 82 + 53\times 50 + 24\times 5 = -1 \mod 89$，這個值更加接近0，因此明文為0

在參考資料[ref. 2]中提供了此加密方案的安全性證明。

2hYan9 日志

@TheFutureIsNow

标签

網絡安全 (45)

动态