1.CW信號
CW可以叫做等幅電報,它通過電鍵控制發信機產生短信號"."(點)和長信號"--"(劃),並利用其不同組合表示不同的字符,從而組成單詞和句子。
CW信號可以看作一種幅度調製信號,類似於幅移鍵控(2ASK信號)其攜帶的信息保存在其幅度中,通過改變載波的幅度來實現基帶數據的傳輸。
其函數表達式如下:
其中:
\(m(t)\):表示基帶信號。
\(cos(2\pi ft + \varphi)\):是調製載波。
2.CW的數字正交解調
原理:
通過正交的方式即可解調出基帶信號,其數學推導如下:
假設基帶信號為\(m(t)\),調製的載波頻率為\(f_1\),解調的載波頻率為\(f_2\),相位為\(\varphi\),LPF為低通濾波器,則:
I路:
根據三角函數公式:
同理:Q路:
為了計算方便假設:
則:
根據三角函數公式:
注:\(arctan\)函數有作用域\((-\pi/2\space\space\space\space\pi/2)\)要求,所以將使用atan2函數替代。
向量旋轉,將一個向量\((cos(\theta_1),sin(\theta_1))\),逆時針旋轉\(\theta_2\),旋轉後的座標為\((cos(\theta_1-\theta_2),sin(\theta_1-\theta_2))\)。將I和Q看着一個向量,將其逆時針旋轉\(arctan(\frac{-Q(t)}{I(t)})\),那麼:
這樣就消除了相位差和頻率差帶來的誤差,\(I'(t)\)就是我們解調的結果。其結果與頻率差與相位差無關。
3.拍頻信號
看過電視劇裏面發電報的應該不陌生,電台在發出或者接收電台信號的時候,經常會聽到滴滴答答的聲音,CW信號如何轉化為音頻信號,就需要通過拍頻器來完成,將電信號轉化為人耳可以識別的聲音信號頻率(20-20000Hz),通過揚聲器播放。
4.MATLAB仿真
仿真代碼:
close all;
fs = 100E3;%採樣率
base_data = [1,0,0,1,0,1,0,0,0,1,1,0,0,1,0];
len = 1E3;
mt = interp1((1:length(base_data)), base_data, (0:length(base_data)/len:length(base_data)-length(base_data)/len), 'nearest');
f_carr_1 = 20E3;%調製載波頻率
f_carr_2 = 21E3;%解調載波頻率
fi = 0.2;%解調載波初始相位
t = 0:1/fs:(len-1)/fs;
cw_data = mt.*cos(2*pi*f_carr_1*t);
I = mt.*cos(2*pi*(f_carr_1-f_carr_2)*t-fi)/2 + randn(size(t))/1000;
Q = -mt.*sin(2*pi*(f_carr_1-f_carr_2)*t-fi)/2 + randn(size(t))/1000;
%% 向量旋轉
theta0 = atan2(Q./(-mt),I./(mt));
It0 = I.*cos(theta0) - Q.*sin(theta0);
Qt0 = Q.*cos(theta0) + I.*sin(theta0);
f_p = 4E3;%拍頻頻率
theta1 = (0:1:length(I)-1)*(f_p*(2*pi)/fs);
It1 = It0.*cos(theta1) ;
%% 保存IQ數據FPGA使用仿真
% fid = fopen('CW.txt','w');
% for i = 1:l
% fprintf(fid,'%d %d\n',floor(I(i)* (2^13)),floor(Q(i)* (2^13)));
% end
% fclose(fid);
%% 繪製
figure
time = 6;
subplot(time,1,1);
plot(mt);
title('基帶數據');
subplot(time,1,2);
plot(cw_data);
title('調製數據');
subplot(time,1,3);
plot(I);
title('I路');
subplot(time,1,4);
plot(Q);
title('Q路');
subplot(time,1,5);
plot(It0);
title('解調數據');
subplot(time,1,6);
plot(It1);
title('解調數據(拍頻)');
結果:
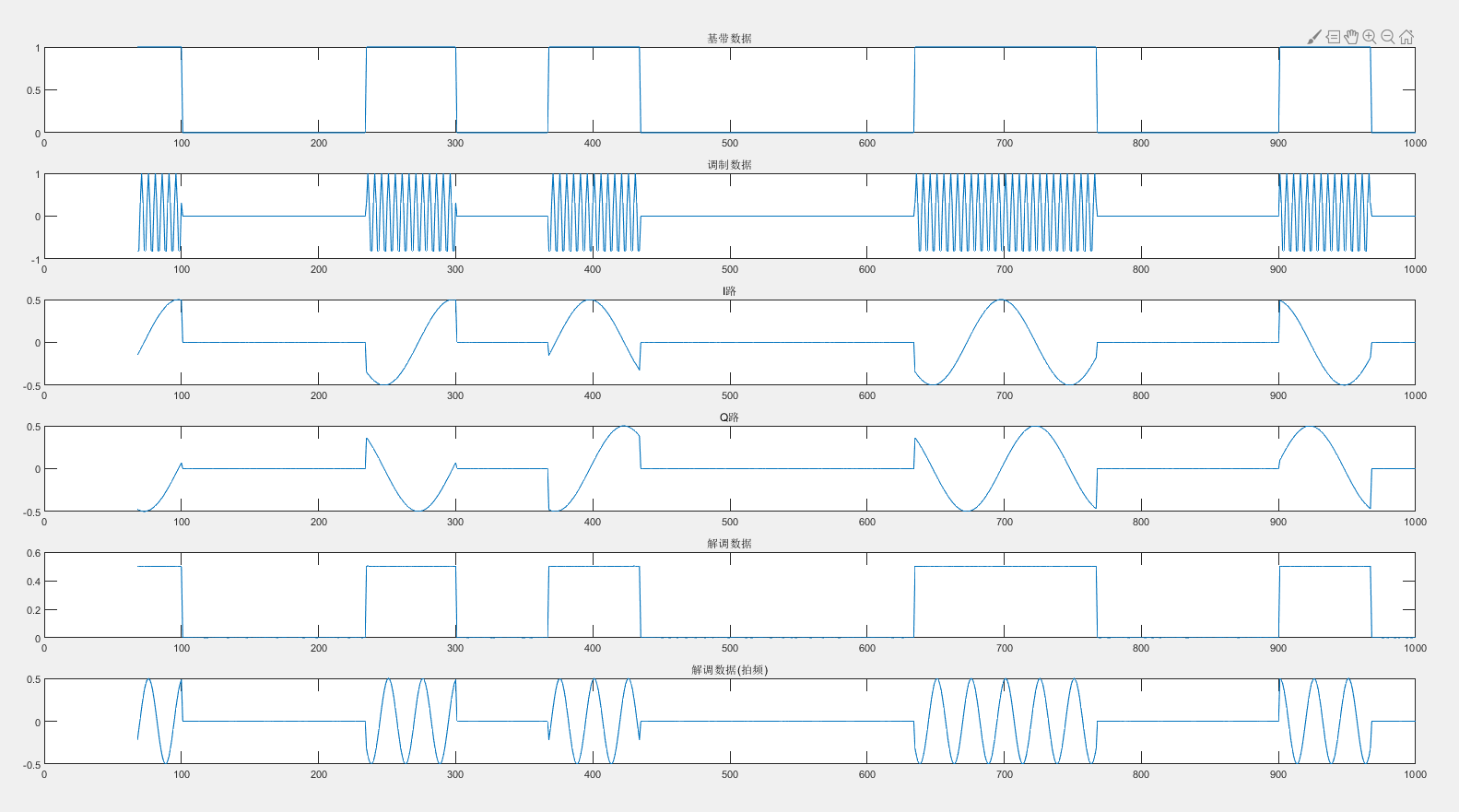
4.FPGA解調
有空補上












