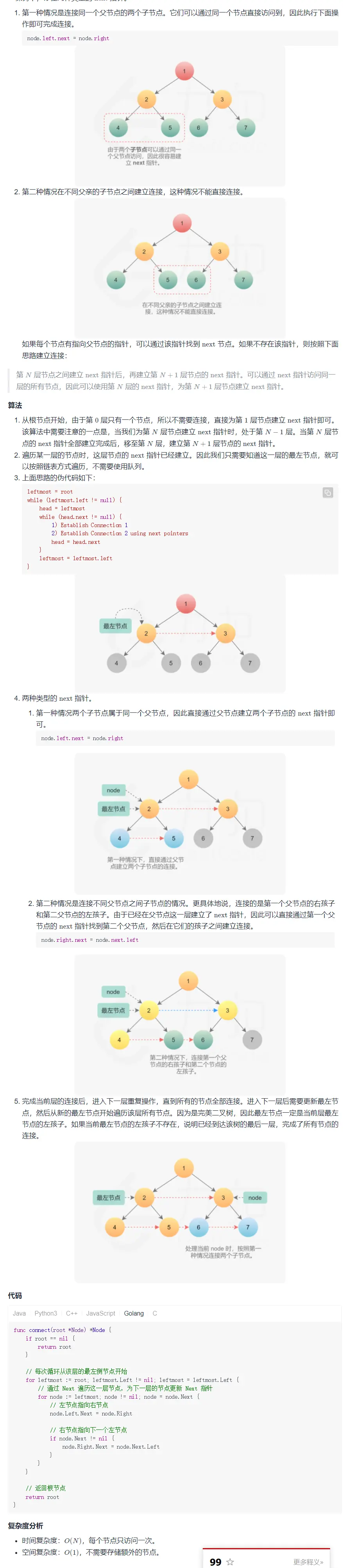
第一題 填充每個節點的下一個右側節點指針

題目

解題思路

由於是在同一層次的操作，本題也可看作為層序遍歷的變種，
只需要在層序遍歷的過程中，加入每一層次節點的串聯即可、

代碼

func connect(root *Node) *Node {
    if root == nil {
        return root
    }

    // 初始化隊列同時將第一層節點加入隊列中，即根節點
    queue := []*Node{root}

    // 循環迭代的是層數
    for len(queue) > 0 {
        tmp := queue
        queue = nil

        // 遍歷這一層的所有節點
        for i, node := range tmp {
            // 連接
            if i+1 < len(tmp) {
                node.Next = tmp[i+1]
            }

            // 拓展下一層節點
            if node.Left != nil {
                queue = append(queue, node.Left)
            }
            if node.Right != nil {
                queue = append(queue, node.Right)
            }
        }
    }

    // 返回根節點
    return root
}

複雜度分析

時間複雜度：O(N)。每個節點會被訪問一次且只會被訪問一次，即從隊列中彈出，並建立 next 指針。

空間複雜度：O(N)。這是一棵完美二叉樹，它的最後一個層級包含 N/2 個節點。廣度優先遍歷的複雜度取決於一個層級上的最大元素數量。這種情況下空間複雜度為 O(N)

優化

BFS使用的數組可以用已連接的上層節點來替代

func connect(root *Node) *Node {
    if root == nil {
        return root
    }

    // 每次循環從該層的最左側節點開始
    for leftmost := root; leftmost.Left != nil; leftmost = leftmost.Left {
        // 通過 Next 遍歷這一層節點，為下一層的節點更新 Next 指針
        for node := leftmost; node != nil; node = node.Next {
            // 左節點指向右節點
            node.Left.Next = node.Right

            // 右節點指向下一個左節點
            if node.Next != nil {
                node.Right.Next = node.Next.Left
            }
        }
    }

    // 返回根節點
    return root
}

作者：LeetCode-Solution
鏈接：https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node/solution/tian-chong-mei-ge-jie-dian-de-xia-yi-ge-you-ce-2-4/
來源：力扣（LeetCode）
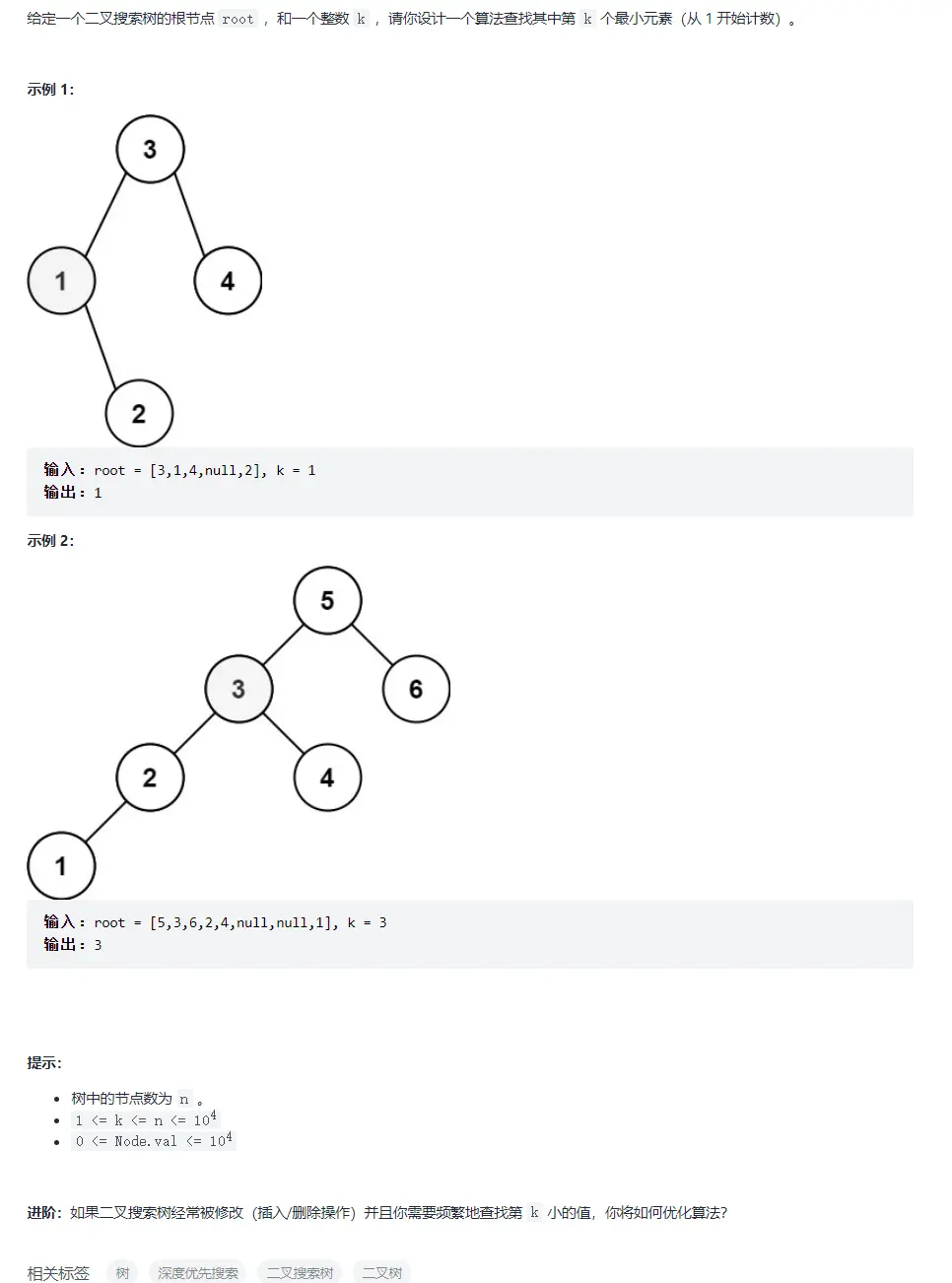
著作權歸作者所有。商業轉載請聯繫作者獲得授權，非商業轉載請註明出處。

第二題 二叉搜索樹中第k小的元素

題目

解題思路

二叉搜索樹的性質為

左子樹的值小於根節點，右子樹的值大於根節點

由此可知，二叉搜索樹的中序遍歷序列即為從小到大排列的有序序列

便可輕易獲取其中第k小的元素

代碼

func kthSmallest(root *TreeNode, k int) int {
    stack := []*TreeNode{}
    for {
        for root != nil {
            stack = append(stack, root)
            root = root.Left
        }
        stack, root = stack[:len(stack)-1], stack[len(stack)-1]
        k--
        if k == 0 {
            return root.Val
        }
        root = root.Right
    }
}

複雜度分析

時間複雜度：O(H+k)，其中 HH 是樹的高度。在開始遍歷之前，我們需要 O(H) 到達葉結點。當樹是平衡樹時，時間複雜度取得最小值 O(logN+k)；當樹是線性樹（樹中每個結點都只有一個子結點或沒有子結點）時，時間複雜度取得最大值 O(N+k)。

空間複雜度：O(H)，棧中最多需要存儲 H 個元素。當樹是平衡樹時，空間複雜度取得最小值 O(logN)；當樹是線性樹時，空間複雜度取得最大值 O(N)

優化（瞭解）