本篇文章以求二叉樹中的最大值和最小值的最大差值為例,記錄一下遞歸中遇到的問題,是遞歸時的參數問題,什麼時候需要把變量放在參數中,什麼時候需要把變量定義為全局變量。
變量定義為全局變量
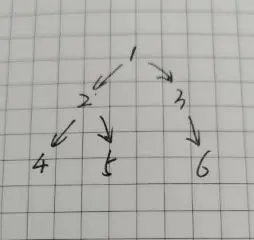
以下面的二叉樹為例,求整棵樹中的節點的值的最大差值,也就是求出最大值和最小值。
前序遍歷的過程如下:
圖中圓圈中記錄的是結點的訪問順序,前序的遍歷順序和訪問順序相同。
走到結點 1 (遍歷結點),記錄下當前的最大值和最小值 [1, 1] (訪問結點),然後遍歷左子樹,遍歷完左子樹再右子樹。
當走到節點 2 時,更新最大值和最小值時,是和 [1, 1] 比較的,所以記錄的最大值和最小值是 [2, 1]。
當走到節點 4 時,更新最大值和最小值時,是和 [2, 1] 比較的,所以記錄的最大值和最小值是 [4, 1]。
當走到節點 5 時,更新最大值和最小值時,是和 [4, 1] 比較的,所以記錄的最大值和最小值是 [5, 1]。
當走到節點 3 時,更新最大值和最小值時,是和 [5, 1] 比較的,所以記錄的最大值和最小值是 [5, 1]。
當走到節點 6 時,更新最大值和最小值時,是和 [5, 1] 比較的,所以記錄的最大值和最小值是 [6, 1]。
遍歷完之後,從節點 4 回到 節點 2 的時候(回溯的時候),最大值和最小值也回到節點 2 時的值 [2, 1] 。所以當遍歷的路徑從 1-2-4 走到 1-2-5 時,節點5 更新最大值和最小值時,是和 [2, 1] 比較的,而不是 [4, 1] 。
下面的代碼是求二叉樹中最大差值,代碼使用java實現前序遍歷。由於最大值和最小值是在整個遍歷過程中對所有節點都是可見的(每次比較的是同一個最大值和最小值),節點會回退,而變量值是不回退的(回溯)。
int diff = 0, max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;
public void getMaxDifference(TreeNode root) {
if (root == null) return;
// 更新最大值、最小值和差值
if (root.val > max) max = root.val;
if (root.val < min) min = root.val;
if (max - min > diff) diff = max - min;
getMaxDifference(root.left);
getMaxDifference(root.right);
}變量作為方法參數
如果是求二叉樹中所有路徑上的差值的最大(每條路徑上都有一個最大值和最小值的差值,求所有路徑中的差值中的最大值)。應該怎麼求呢??
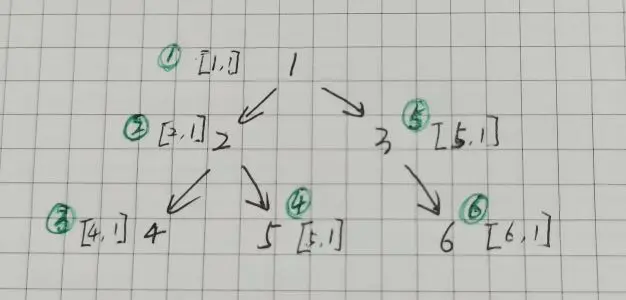
下面的圖中是前序遍歷的過程。和上面前序遍歷過程不同的是,這次每個節點中更新最大值和最小值時,比較的值是該條路徑上的最大值和最小值,而不是二叉樹中所有節點中的最大值和最小值。
圖中,[最大值,最小值] 記錄的訪問當前節點時的最大值和最小值,綠色線是從上到下遍歷時走的路線,紅色線是節點回退時走的路線。
當走到節點 4 時,記錄的最大值和最小值是 [4, 1]。遍歷完之後,從節點 4 回到 節點 2 的時候(回溯的時候),最大值和最小值也回到節點 2 時的值 [2, 1] 。所以當遍歷的路徑從 1-2-4 走到 1-2-5 時,節點5 更新最大值和最小值時,是和 [2, 1] 比較的,而不是 [4, 1] 。
同理,節點 3 更新最大值和最小值時,是和 [1, 1] 比較的,而不是 [5, 1] , 所以它記錄的值是 [3, 1]。
節點 6 更新最大值和最小值時,是和 [3, 1] 比較的, 所以它記錄的值是 [6, 1]。
從遍歷的過程中,發現更新最大值和最值時比較的值並不是全局中求得的最大值和最小值,因為最大值和最小值並不是全局的而是在遍歷完之後就會消失,所以,需要修改上面的代碼
int diff = 0; // 差值
public void getMaxDifference(TreeNode root, int max, int min) {
// 遍歷到空節點,一條路徑走完,記錄這條路徑的結果
if (root == null){
if (max - min > diff) diff = max - min; // 更新差值
return;
}
// 更新最大值、最小值(它們的值只作用於此次遞歸,遞歸結束後就消失)
if (root.val > max) max = root.val;
if (root.val < min) min = root.val;
getMaxDifference(root.left, max, min);
getMaxDifference(root.right, max, min);
}遞歸時棧中元素變化
在遞歸時,每一次遞歸會把本次遞歸的局部變量等壓入棧中,在遞歸結束後會把局部變量再彈出棧,所以遞歸結束後,是沒有值的。遞歸中間的值是不保存的。
所以,前序遍歷過程中棧中元素的變化如下:
| 結點 | 遞歸時入棧後棧 | 遞歸結束後出棧 |
|---|---|---|
| 1 | [1,1] | [] |
| 2 | [1,1], [2,1] | [1,1] |
| 4 | [1,1], [2,1], [4,1] | [1,1], [2,1] |
| 5 | [1,1], [2,1], [5,1] | [1,1], [2,1] |
| 3 | [1,1], [3,1] | [1,1] |
| 6 | [1,1], [3,1], [6,1] | [1,1], [3,1] |
另外要説的一點是,基本類型作為方法參數,在方法內改變參數的值,是不能影響方法外的值的。參數的作用範圍只在方法內。所以下面的代碼是無效的
// 交換兩個整數
public void swap(int a, int b) {
int t = a;
a = b;
b = t;
}
public void test() {
int a = 3, b = 4;
swap(a, b);
// a 還是 3, b 還是 4,並不是真的發生交換
}