先大概説一下二叉樹的基本內容。

1. 二叉樹

什麼是二叉樹？

二叉樹是一種樹形結構，每個結點最多兩棵子樹，而且子樹有左右之分，次序不能顛倒。左右子樹也是一棵二叉樹。

1.1 二叉樹的存儲

二叉樹可以用數組和鏈表存儲。

1）順序存儲

使用一組地址連續的存儲單元依次自上而下，自左而右的順序存儲二叉樹上的結點。簡單來説，就是用數組存儲，存二叉樹的順序是從上到下，從左到右。

順序存儲方式適合完全二叉樹或滿二叉樹。因為數組的長度是固定的，而這種二叉樹的空節點少，不會浪費很多數組的地址空間。

// java 定義方式
int[] array = new int[3];
array[0] = 1;
array[2] = 3;
// 或者是
int[] array = {1, 0, 3};  // 0 表示該處節點為空

2）鏈式存儲

由於一般二叉樹會有很多節點為空，如果使用順序存儲會導致很多空間浪費掉。所以一般的二叉樹使用鏈式存儲比較多。大多情況下，用到的也是鏈式存儲，比如經常使用到的遍歷。

鏈式存儲是使用鏈表節點來存儲二叉樹中的每個節點。所有需要先定義鏈表的結點。

// java 定義方式
class TreeNode {
    int val;
    TreeNode left, right;
    // 構造函數
}

1.2 二叉樹的遍歷

二叉樹的遍歷方法：前序遍歷、中序遍歷、後序遍歷，應該沒有人不知道。以下的代碼是使用java實現

1）前序遍歷

void preOrder(TreeNode root) {
    // 終止條件
    if (root == null) return;
    getValue(root);  // 訪問該結點，做一些計算等
    preOrder(root.left); // 遍歷左結點點
    preOrder(root.right);  // 遍歷右結點
}

2）中序遍歷

void preOrder(TreeNode root) {
    // 終止條件
    if (root == null) return;
    preOrder(root.left); // 遍歷左結點點
    getValue(root);  // 訪問該結點，做一些計算等
    preOrder(root.right);  // 遍歷右結點
}

3）後序遍歷

void preOrder(TreeNode root) {
    // 終止條件
    if (root == null) return;
    preOrder(root.left); // 遍歷左結點點
    preOrder(root.right);  // 遍歷右結點
    getValue(root);  // 訪問該結點，做一些計算等
}

4）例子

這三種遍歷方法的代碼並不難，平常做題的時候也沒有很大的問題。但是有一次在極度緊張下，我發現做題時竟然分不清當時用的是哪種遍歷，是前序還是中序還是回溯來着？？是該用哪種寫代碼呢？？

以求樹中的最大值、最小值為例。有這樣一棵樹，通過遍歷的方式求出二叉樹中的最大值、最小值。

那麼，在遍歷中，需要記錄當前結點的最大值和最小值，下面的圖中，[最大值, 最小值] 記錄的是當前的最大值和最小值。

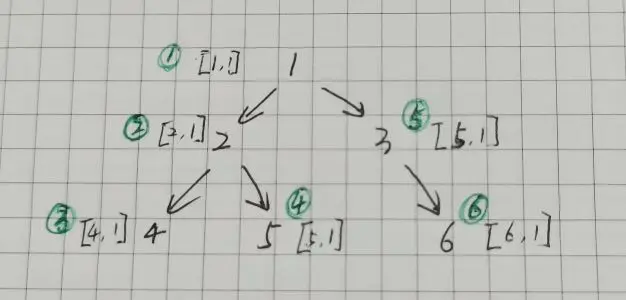
前序遍歷

走到結點 1 （遍歷結點），記錄下當前的最大值和最小值 [1, 1] （訪問結點），然後遍歷左子樹，遍歷完左子樹再右子樹。圖中圓圈中記錄的是結點的訪問順序，前序的遍歷順序和訪問順序相同。

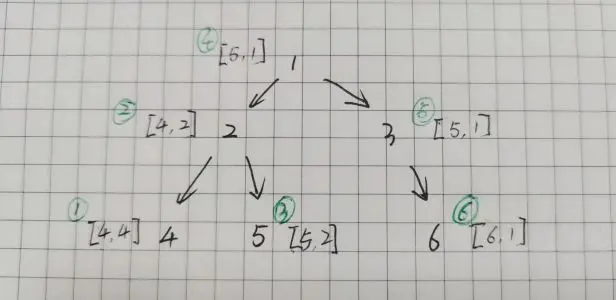
中序遍歷

以結點 1 為例，走到結點 1 （遍歷結點），不記錄。當把左子樹的節點訪問完之後，然後訪問結點 1，也就是記錄結點 1 此時的最大值最小值 [5, 1] 。然後再訪問結點 1 的右子樹。

所以，第一個記錄最大值和最小值的結點是結點 4 ，也就是第一個訪問的結點是結點 4 。第二個記錄最大值和最小值的結點是結點 2 ，也就是第二個訪問的結點是結點 2 。

圖中圓圈中記錄的是結點的訪問順序，中序的遍歷順序和訪問順序不同。

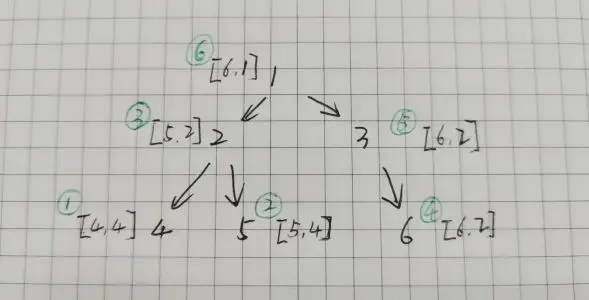
後序遍歷

以結點 1 為例，走到結點 1 （遍歷結點），不記錄。當把左子樹的節點訪問完之後，然後再訪問結點 1 的右子樹。最後訪問結點 1 ，也就是記錄結點 1 此時的最大值最小值 [6, 1] 。

所以，第一個記錄最大值和最小值的結點是結點 4 ，也就是第一個訪問的結點是結點 4 。第二個記錄最大值和最小值的結點是結點 5 ，也就是第二個訪問的結點是結點 5 。

圖中圓圈中記錄的是結點的訪問順序，後序的遍歷順序和訪問順序不同。

遍歷順序的問題就到這裏了。下面的代碼是求二叉樹中的最大值和最小值，代碼使用java實現。

int max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;
public void getMaxDifference(TreeNode root) {
    if (root == null) return;
    
    if (root.val > max) max = root.val;
    if (root.val < min) min = root.val;
   
    getMaxDifference(root.left);
    getMaxDifference(root.right);
}

4）層次遍歷

層次遍歷是通過隊列實現的，以下的代碼是使用java實現

// 遍歷二叉樹，其他什麼也沒做
void level(TreeNode root) {
    LinkedList<TreeNode> queue = new LinkedList<>();
    if (root != null) queue.offer(root);  // 加入根節點
    while (!queue.isEmpty()) {
        // 彈出隊首節點
        TreeNode cur = queue.poll();  
        // 加入左右節點
        if(cur.left != null) queue.offer(cur.left);
        if(cur.right != null) queue.offer(cur.right);
    }
}

2. 樹

二叉樹是樹，但樹不一定是二叉樹。所以，二叉樹和樹的關係就很明顯：二叉樹可以使用樹的東西，樹不能使用二叉樹的東西。

為什麼這裏會説到樹呢？

因為在一次面試中遇到一道題，是使用數組存儲二叉樹，數組中的值是它的父節點的下標。嗯嗯，如果把二叉樹和樹割裂開記憶學習，思維會侷限在那一小塊。不只是二叉樹和樹，其他的知識也應該聯繫在一起，也可以聯繫在一起。

2.1 樹的存儲方式

樹的存儲方式有很多中，即可用順序存儲，也可用鏈式存儲。但是不管哪種存儲方式，都要能夠唯一的反映樹中各節點之間的邏輯關係。這一點，對於二叉樹來説也是一樣。因為樹中有幾個子節點，是不確定的，所以不能像二叉樹中那樣，直接定義兩個子節點 left， right ，就可以表示整個樹。

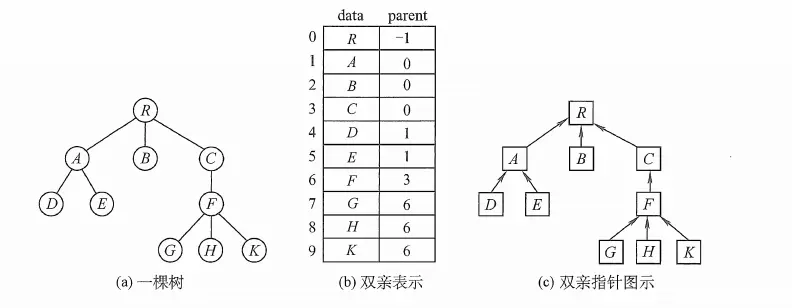
1）雙親表示法

記錄的是當前節點的父結點。使用數組存儲，存儲的是當前節點的父節點在數組中的位置。

正式點的術語説就是，採用一組連續空間來存儲每個節點，同時每個節點增加一個變量（指針），用來記錄該節點的雙親節點在數組中的位置。

這種結構，找到當前結點的父節點很容易，但是找到當前結點的孩子節點，需要遍歷整個樹，也就整個存儲結構。

上面的樹的存儲結構，可以表示為以下（使用 java 實現）

// 定義結點
class TreeNode {
    int val;
    int parent;
    // 構造函數
}
// 定義一棵樹
TreeNode[] tree = new TreeNode[10];

如果一棵樹中節點的值就是數組中的下標，那麼還可以不存儲 val ，表示如下（使用 java 描述）

int[] tree = new int[10];

舉個例子，如果一個數組是 int[] tree = {1, -1, 1, 0} ，那麼這棵樹表示的就是，根節點是 1， 1 的兩個子節點是 0 ，2 ， 0 的一個子節點是 3 。

嗯嗯嗯，這個好像是二叉樹？？嗯，就是二叉樹，用數組表示了一棵普通的二叉樹（當然了，這種表示方式不能區分左右子節點）。

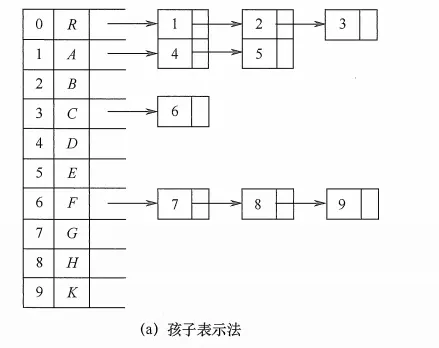
2）孩子表示法

記錄的是當前節點的所有子結點。

正式點的術語説就是，每個結點的孩子都用單鏈表連接起來，形成一個線性結構，

這種結構，找到當前結點的孩子節點很容易，但是找到當前結點的父節點，需要遍歷整個樹，也就整個存儲結構。

上面的樹的存儲結構，可以表示為以下（使用 java 實現）

// 定義結點
class TreeNode {
    int val;
    List<TreeNode> child;
    // 構造函數
}
// 定義一棵樹
TreeNode[] tree = new TreeNode[10];

如果一棵樹中節點的值就是數組中的下標，那麼還可以不存儲 val ，表示如下（使用 java 描述）

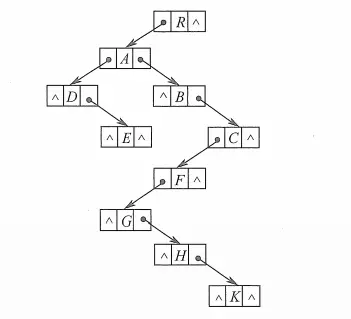
List<Integer>[] tree = new List[10];

3）孩子兄弟表示法

記錄的是當前節點的第一個子結點和下一個兄弟節點。孩子兄弟表示法又稱二叉樹鏈表法， 也就是將二叉鏈表作為樹的存儲結構，一個子結點指向孩子結點，一個子結點指向兄弟節點。

上面的樹的存儲結構，可以表示為以下（使用 java 實現）

// 定義結點
class TreeNode {
    int val;
    TreeNode firstChild, nextsibling;
    // 構造函數
}
// 定義一棵樹
TreeNode[] tree = new TreeNode[10];

參考資料

王道數據結構書籍