閲讀指南：

1. 省流總結部分直接記錄了博客的takeaway，適合快速確認是否適合閲讀本文章 or 後續快速温習
2. 博客正文從省流總結部分後開始

省流總結

數學分析部分

數學概念

線性模型可以看作對輸入特徵的一次 仿射變換 (affine transformation)。
仿射變換由兩部分組成：

1. 線性變換：對特徵施加一個線性映射 (權重矩陣／向量)

2. 平移：再加上一個常數偏置項 (bias)

   線性模型的定義

   線性模型的預測公式：$$ \boxed{\underset{n\times 1}{\mathbf y_{\text{pred}}} =\; \underbrace{X}_{n\times d}\; \underbrace{\mathbf w}_{d\times 1}\; +\; \underbrace{\mathbf 1}_{n\times 1}\; \underbrace{b}_{1\times1}} $$

   模型優化

   在假定數據集噪聲服從高斯分佈的情況下，我們採用 L2（均方誤差）損失，通過最小化損失函數來達到訓練目標：
   $$ \boxed{L(\mathbf w,b) =\frac12\, \bigl\|\,\mathbf y_{\text{pred}}-\mathbf y_{\text{true}}\bigr\|_{2}^{2}} = \frac12\left\| X\mathbf w+\mathbf 1\,b-\mathbf y_{\text{true}} \right\|^{2} $$

損失 \(L\) 為二次凸函數，對 \(\mathbf w,b\) 全局可微。 因此 梯度為零是必要且充分條件（凸優化）。因此，通過求解\(L(\mathbf w,b)\)對\(\mathbf w\)與b的偏導等於0，我們可以求解出最優模型參數\(\mathbf w,b\)。
對 \(\mathbf w\) 求偏導有：$$ \nabla_{\mathbf w}L = \frac{\partial L}{\partial\mathbf w} = X^{\top}\bigl(X\mathbf w+\mathbf 1\,b-\mathbf y_{\text{true}}\bigr) = \mathbf 0_{d\times1} $$ 對 \(b\) 求偏導有： $$ \frac{\partial L}{\partial b} = \mathbf 1^{\top}\bigl(X\mathbf w+\mathbf 1\,b-\mathbf y_{\text{true}}\bigr) = 0_{1\times1} $$ 解此方程組即可得到最優解 \( (\mathbf w^*, b^*) \)。

對於模型解析解 (Normal Equation) 的求解，我們使用“增廣”技巧以吸收掉數學模型方程中的 \(b\) 項

通過增廣特徵矩陣和權重向量，我們可以把模型寫作如下形式： $$\underset{n\times (d+1)}{\tilde X}= \bigl[\mathbf 1,\;X\bigr], \underset{(d+1)\times1}{\tilde{\mathbf w}}= \begin{bmatrix} b\\\mathbf w \end{bmatrix}, \; \mathbf y_{\text{pred}} = \tilde X\,\tilde{\mathbf w} $$
因此簡單的求解析解 \(\mathbf w\) 偏導數為0可以得到如下解

$$ \boxed{\tilde{\mathbf w}^{*} = \bigl(\tilde X^{\top}\tilde X\bigr)^{-1}\tilde X^{\top}\mathbf y_{\text{true}}} $$

隨機梯度下降方法的核心思想就是選取一個批次求平均梯度（而不是求整個數據集的完整梯度），然後依據平均梯度進行小量更新。下面是SGD在線性模型上的更新公式，其中 \(\eta\) 為學習率 (learning rate)。 上述公式可以等價的寫為如下表達式，其中 \(|\mathcal B|\) 表示一個batch中的樣本數量：
$$ \boxed{ \begin{cases} \mathbf w \;\leftarrow\; \mathbf w-\frac{\eta}{|\mathcal B|}\sum_{i\in\mathcal B}\mathbf x^{(i)}\bigl(y_{\text{pred}}^{(i)}-y_{\text{true}}^{(i)}\bigr)\\[6pt] b \;\leftarrow\; b-\frac{\eta}{|\mathcal B|}\sum_{i\in\mathcal B}\bigl(y_{\text{pred}}^{(i)}-y_{\text{true}}^{(i)}\bigr) \end{cases}} $$
一個更通用的更新形式如下：

$$ \begin{cases} \mathbf w \leftarrow \mathbf w - \eta\,\nabla_{\mathbf w} L_{\mathcal{B}} \\[6pt] b \leftarrow b - \eta\,\displaystyle\frac{\partial L_{\mathcal{B}}}{\partial b} \end{cases} $$

核心問題回答

1. 為什麼令損失函數的偏導數為 \(0\) 就能求出最優參數？

1. 一階必要條件（First-Order Necessary Condition） ：若可微函數在某點取得極值（極小 / 極大 / 鞍點），其梯度必須為零。
2. 充分性通常依賴於目標函數的性質：對 凸 損失而言，任何駐點（梯度為零的點）都是全局最小點；若進一步滿足 Hessian 正定，則最小值唯一。

2. 為什麼選擇 L2 損失函數作為最小化目標？
   我們假設對於每個樣本，都存在噪聲 \(\varepsilon \sim \mathcal N(0,\sigma^{2})\)，即有

$$ y_{true} = \mathbf w^\top \mathbf x + b + \varepsilon $$

注：正態分佈 \(\mathcal N(\mu, \sigma^2)\) 的概率密度函數為

$$ p(x) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp\Bigl(-\frac{(x-\mu)^{2}}{2\sigma^{2}}\Bigr). $$

使用極大似然法則，我們可以寫出通過給定的 \(\mathbf x\) 觀測到特定 \(y\) 的 似然（likelihood）：

$$ p\bigl(y^{(i)}\mid\mathbf x^{(i)},\mathbf w,b\bigr) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp\Bigl(-\frac{\bigl(y^{(i)}-\mathbf w^\top\mathbf x^{(i)}-b\bigr)^{2}}{2\sigma^{2}}\Bigr) = \mathcal N\bigl(y^{(i)} \mid \mathbf w^\top\mathbf x^{(i)}+b,\, \sigma^{2}\bigr). $$

整批樣本獨立同分布，故 整體似然 為：

$$ P(\mathbf y\mid X,\mathbf w,b) = \prod_{i=1}^{n}p\bigl(y^{(i)}\mid\mathbf x^{(i)},\mathbf w,b\bigr). $$

最大化整體似然等價於最小化負對數似然：

$$ -\log P(\mathbf y\mid X,\mathbf w,b) = \frac{n}{2}\log(2\pi\sigma^{2}) + \frac{1}{2\sigma^{2}}\sum_{i=1}^{n}\bigl(y^{(i)}-\mathbf w^\top\mathbf x^{(i)}-b\bigr)^{2}. $$

由於我們希望求的參數是 \(\mathbf w, b\)，因此移除無關的常數項（不影響極值點求解），我們將問題轉化為：尋找參數 \(\mathbf w, b\) ，使其最小化如下表達式（也就是L2損失函數）

$$ \mathcal L(\mathbf w,b) = \frac{1}{2}\lVert X\mathbf w+b\mathbf 1-\mathbf y\rVert_{2}^{2}, $$

注： \(\lVert\cdot\rVert_{2}\)表示 二範數（L-2 範數 / Euclidean norm）。給定向量 \(\mathbf v\in\mathbb R^{n}\)，其 2-範數定義為

$$ \lVert \mathbf v\rVert_{2}= \sqrt{\sum_{i=1}^{n} v_{i}^{2}} $$

因此上述表達式可以改寫為求殘差的平方和，也就是：

$$ \bigl\lVert X\mathbf w+b\mathbf 1-\mathbf y\bigr\rVert_{2}^{2} =\Bigl(\sqrt{\sum_{i=1}^{n}\bigl(x_i^{\mathsf T}\mathbf w+b-y_i\bigr)^{2}}\Bigr)^{2} =\sum_{i=1}^{n}\bigl(x_i^{\mathsf T}\mathbf w+b-y_i\bigr)^{2}, $$

2.2 為什麼估測噪聲為正態分佈？

1. 中心極限定理 (Central Limit Theorem)
   實際測量誤差通常由大量獨立的小擾動之和構成；當這些擾動無偏且具有有限方差時，其總和將在樣本量足夠大時趨向正態分佈。
2. 最大熵原理 (Maximum Entropy Principle)
   在僅已知誤差的期望為零、方差為 \(\sigma^{2}\) 的前提下，信息最少（熵最大）的分佈就是高斯分佈。若沒有更多先驗信息，選擇正態噪聲是最不帶偏見也最符合"奧卡姆剃刀"的假設。

當我們不知道 \(\varepsilon\) 的真實分佈時，選擇正態噪聲不會引入額外偏差。擔當我們對噪聲分佈存在先驗知識時，可以假定數據集噪聲服從其它分佈。

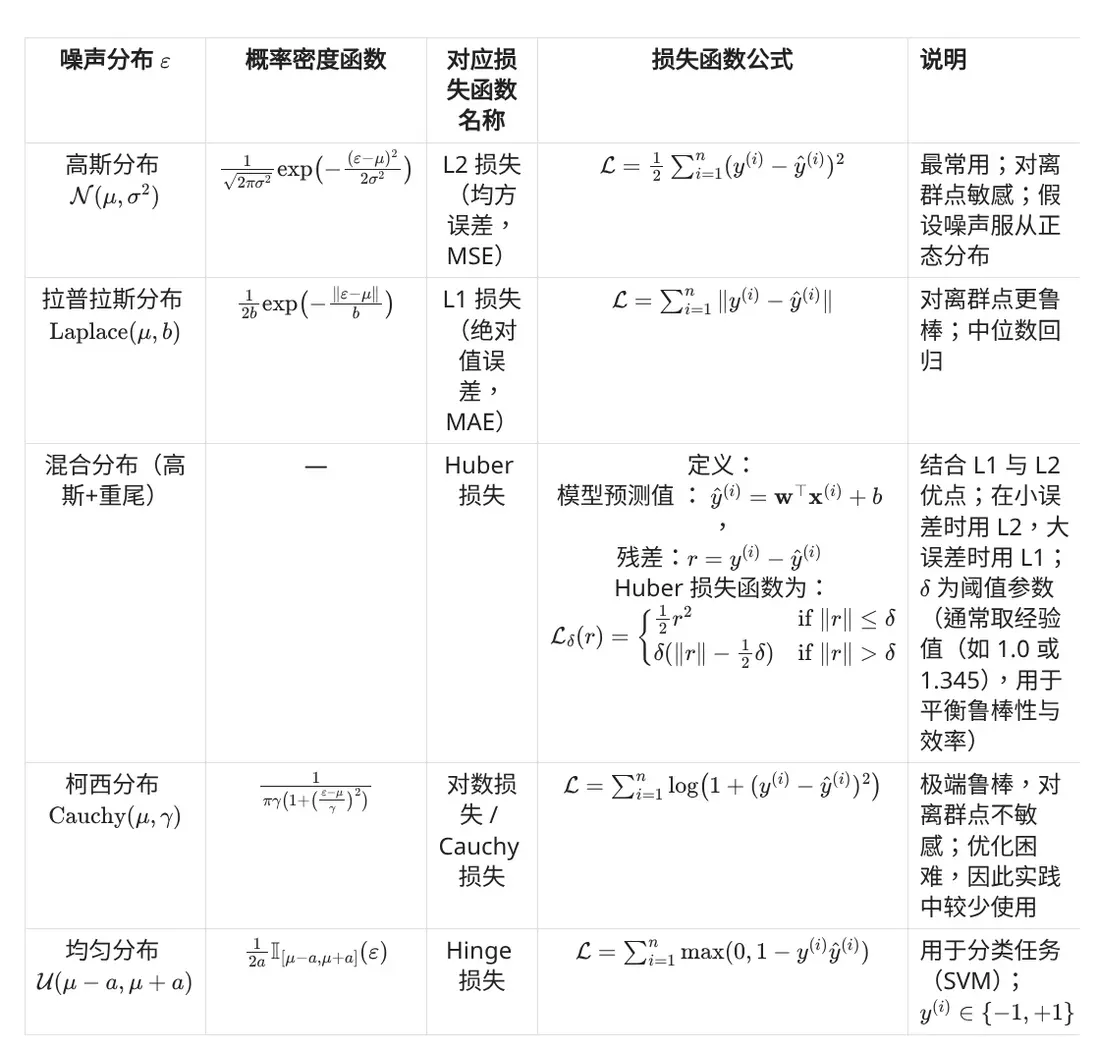
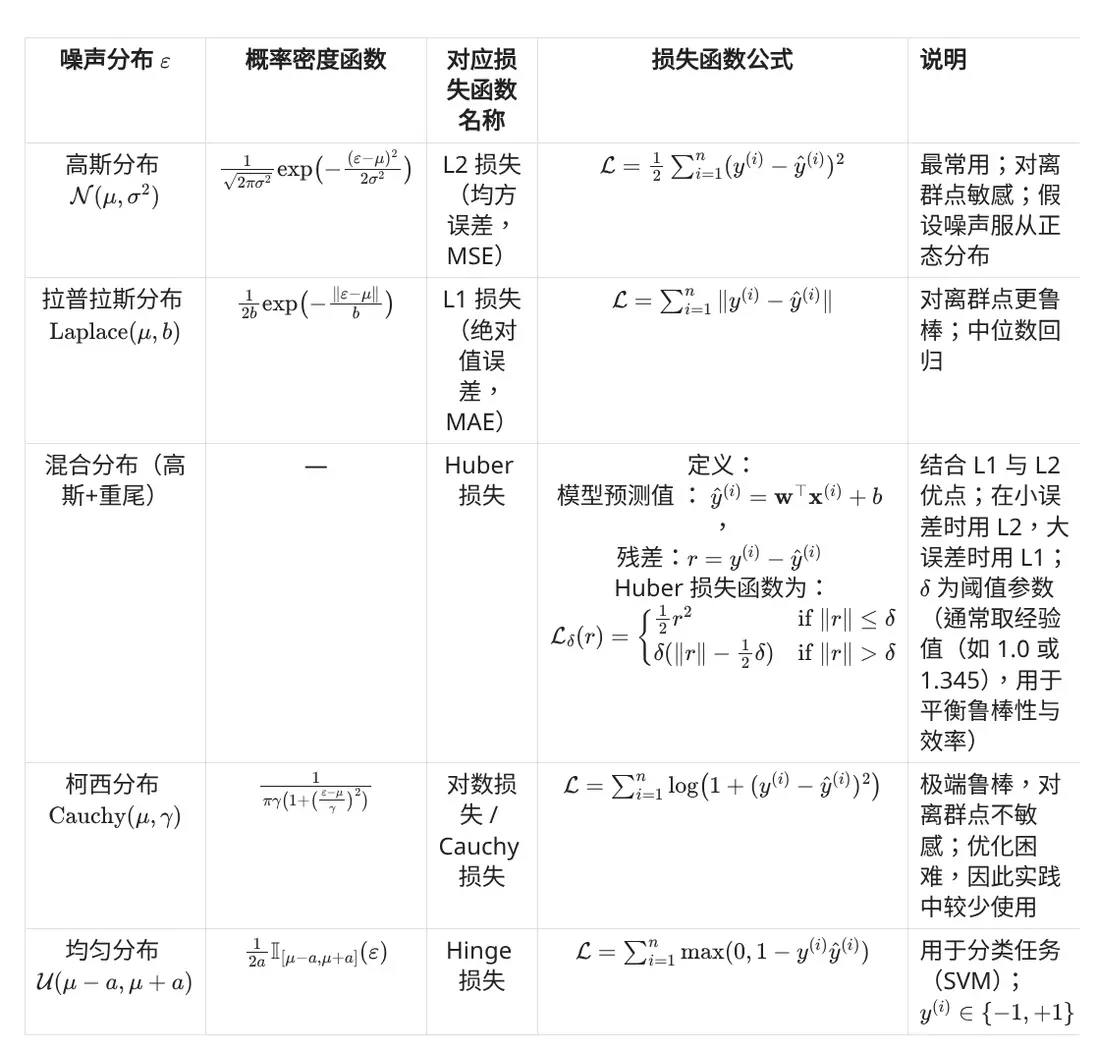
噪聲分佈與損失函數關係如下表所示

代碼實現部分

一般我們會用自動微分+torch迅速秒一個，不會手敲求出來的那個backward更新的（自動微分已確保能夠自動求出），故略。

總結啓發部分

1. 損失函數的選擇與假定的噪聲分佈有關，可以假定數據集噪聲服從其它分佈。
2. 損失函數的性質將會影響優化容易程度

參考資料

3.1. 線性迴歸 — 動手學深度學習 2.0.0 documentation

前置知識

1. 微積分：導數
2. 概率論與數理統計：極大似然法則

3. 線性代數：矩陣運算

   線性模型教學

   數學知識

   線性模型可以看作對輸入特徵的一次 仿射變換 (affine transformation)。
   仿射變換由兩部分組成：

4. 線性變換：對特徵施加一個線性映射 (權重矩陣／向量)
5. 平移：再加上一個常數偏置項 (bias)

預測階段（Forward Pass）

設單個樣本的特徵維度為 \(d\)，我們按列向量書寫（假設向量所有元素 \(c\) 均滿足 \(c \in R\)： $$ \underset{d\times1}{\mathbf w},\quad \underset{d\times1}{\mathbf x},\quad \underset{1\times1}{b},\quad \underset{1\times1}{y_{\text{pred}}},\quad \underset{1\times1}{y_{\text{true}}} $$ 線性模型的輸出為 $$ \boxed{y_{\text{pred}} = \underbrace{\mathbf w^{\top}}_{1\times d} \; \underbrace{\mathbf x}_{d\times 1} \;+\; \underbrace{b}_{1\times1}}$$
從直觀的理解上，我們希望 \(\;y_{\text{pred}}\;\) 與 \(\;y_{\text{true}}\;\) 儘可能接近。在最好的情況下，我們希望對於每個樣本，都有\(y_{pred} = y_{true}\) 。然而由於數據集內存在噪聲，這一目標不可能實現。我們必須選取一系列指標以刻畫 \(y_{pred}\) 與 \(y_{true}\) 的 接近程度。在迴歸任務中，這一指標便是L2損失函數，訓練階段我們將對此做詳細討論。

訓練階段（Learning / Fitting）

回顧：機器學習訓練的本質：
在給定數據集 \((X,\; \mathbf y_{\text{true}})\) 的前提下，通過最優化方法尋找模型最優參數（對於線性模型，其參數為 \((\mathbf w,b)\)），使得整體損失最小。
因此，我們給出如下的線性模型數學表述

形式化表述

輸入數據矩陣：
$$\underset{n\times d}{X}=\bigl[\mathbf x^{(1)},\dots,\mathbf x^{(n)}\bigr]^{\top}$$
目標向量：
$$\underset{n\times1}{\mathbf y_{\text{true}}}=\bigl[y^{(1)},\dots,y^{(n)}\bigr]^{\top}$$權重向量、偏置向量與全1列向量：$$\underset{d\times1}{\mathbf w}, \underset{1\times1}{b}, \underset{n\times1}{\mathbf 1}$$
模型對全部樣本的輸出為 $$ \boxed{\underset{n\times 1}{\mathbf y_{\text{pred}}} =\; \underbrace{X}_{n\times d}\; \underbrace{\mathbf w}_{d\times 1}\; +\; \underbrace{\mathbf 1}_{n\times 1}\; \underbrace{b}_{1\times1}} $$

損失函數

我們採用 L2（均方誤差）損失：
$$ \boxed{L(\mathbf w,b) =\frac12\, \bigl\|\,\mathbf y_{\text{pred}}-\mathbf y_{\text{true}}\bigr\|_{2}^{2}} = \frac12\left\| X\mathbf w+\mathbf 1\,b-\mathbf y_{\text{true}} \right\|^{2} $$ 我們希望找到模型參數\((\mathbf w,b)\)，使得對於整個數據集，損失函數 \(L(\mathbf w,b)\)最小。也就是有訓練目標：
$$ \min_{\mathbf w,b}\; L(\mathbf w,b) \quad\Longleftrightarrow\quad \operatorname*{arg\,min}_{\mathbf w,b}L(\mathbf w,b) $$

求解模型參數

由凸優化理論可知，損失 \(L\) 為二次凸函數，對 \(\mathbf w,b\) 全局可微。 因此 梯度為零是必要且充分條件（凸優化）。因此，通過求解\(L(\mathbf w,b)\)對\(\mathbf w\)與b的偏導等於0，我們可以求解出最優模型參數\(\mathbf w,b\)

對 \(\mathbf w\) 求偏導有：$$ \nabla_{\mathbf w}L = \frac{\partial L}{\partial\mathbf w} = X^{\top}\bigl(X\mathbf w+\mathbf 1\,b-\mathbf y_{\text{true}}\bigr) = \mathbf 0_{d\times1} $$ 對 \(b\) 求偏導有： $$ \frac{\partial L}{\partial b} = \mathbf 1^{\top}\bigl(X\mathbf w+\mathbf 1\,b-\mathbf y_{\text{true}}\bigr) = 0_{1\times1} $$ 解此方程組即可得到最優解 \((\mathbf w^*, b^*)\)。

模型解析解 (Normal Equation)

線性模型是可以求出最優解 \((\mathbf w^*, b^*)\)的解析解的。下面給出數學分析：

為了簡化符號，我們引入“增廣”技巧以吸收掉數學模型方程中的 \(b\) 項：

1. 增廣特徵矩陣： $$\underset{n\times (d+1)}{\tilde X}= \bigl[\mathbf 1,\;X\bigr]$$
2. 增廣權重向量： $$\underset{(d+1)\times1}{\tilde{\mathbf w}}= \begin{bmatrix} b\\\mathbf w \end{bmatrix} $$
   隨後，我們便可以把模型寫成 $$ \mathbf y_{\text{pred}} = \tilde X\,\tilde{\mathbf w} $$
   損失變為 $$ L(\tilde{\mathbf w}) = \frac12\bigl\|\tilde X\tilde{\mathbf w}-\mathbf y_{\text{true}}\bigr\|^{2}. $$ 我們令損失函數對 \(\tilde{\mathbf w}\) 的偏導數為0，即有：$$ \tilde X^{\top}\bigl(\tilde X\tilde{\mathbf w}-\mathbf y_{\text{true}}\bigr)=\mathbf 0 $$ 若 \(\tilde X^{\top}\tilde X\) 滿秩，則可以移項得 $$ \boxed{\tilde{\mathbf w}^{*} = \bigl(\tilde X^{\top}\tilde X\bigr)^{-1}\tilde X^{\top}\mathbf y_{\text{true}}} $$ 還原回原有符號表述，展開可得：$$ \boxed{ \begin{cases} \underset{d\times1}{\mathbf w^{*}} = \bigl( \underset{d\times n}{X^{\top}}\; \underset{n\times n}{H}\; \underset{n\times d}{X} \bigr)^{-1} \; \underset{d\times n}{X^{\top}}\; \underset{n\times n}{H}\; \underset{n\times1}{\mathbf y_{\text{true}}}, \\[10pt] \underset{1\times1}{b^{*}} = \underset{1\times1}{\bar y} - \underset{1\times d}{\bar{\mathbf x}^{\!\top}} \; \underset{d\times1}{\mathbf w^{*}} \end{cases}} $$ 其中： $$ \underset{n\times n}{H} = I_{n} - \frac1n \underset{n\times1}{\mathbf 1}\; \underset{1\times n}{\mathbf 1^{\!\top}} \qquad\text{（中心化投影矩陣）} $$ $$ \underset{1\times1}{\bar y} = \frac1n\, \underset{1\times n}{\mathbf 1^{\!\top}}\; \underset{n\times1}{\mathbf y_{\text{true}}}, \qquad \underset{d\times1}{\bar{\mathbf x}} = \frac1n\, \underset{d\times n}{X^{\top}}\; \underset{n\times1}{\mathbf 1} $$

隨機梯度下降（SGD）實現

當 \(n\) 或 \(d\) 巨大時，計算 \((\tilde X^{\top}\tilde X)^{-1}\) 代價高昂，因此解析解往往並不常用。一般的，我們 SGD （Mini-batch GD ）迭代優化得最優參數：

1. 初始化 \(\mathbf w, b\)（如隨機）
2. 對每個 mini-batch \(\bigl(X_{\mathcal B},\mathbf y_{\mathcal B}\bigr)\) 執行 $$\begin{aligned} \text{計算}&\;\; \mathbf y_{\text{pred}}^{(\mathcal B)} = X_{\mathcal B}\mathbf w+\mathbf 1 b \\[4pt] \text{殘差}&\;\; \mathbf r = \mathbf y_{\text{pred}}^{(\mathcal B)}-\mathbf y_{\mathcal B} \\[4pt] \text{梯度}&\;\; \begin{cases} \nabla_{\mathbf w} L_{\mathcal B} = X_{\mathcal B}^{\top}\mathbf r \\[6pt] \displaystyle\frac{\partial L_{\mathcal B}}{\partial b} = \mathbf 1^{\top}\mathbf r \end{cases}\\[10pt] \text{參數更新}&\;\; \begin{cases} \mathbf w\leftarrow \mathbf w -\eta\,\nabla_{\mathbf w} L_{\mathcal B}\\[6pt] b\leftarrow b -\eta\,\displaystyle\frac{\partial L_{\mathcal B}}{\partial b} \end{cases} \end{aligned}$$ 其中 \(\eta\) 為學習率 (learning rate)。 上述公式可以等價的寫為如下表達式，其中 \(|\mathcal B|\) 表示一個batch中的樣本數量：
   $$ \boxed{ \begin{cases} \mathbf w \;\leftarrow\; \mathbf w-\frac{\eta}{|\mathcal B|}\sum_{i\in\mathcal B}\mathbf x^{(i)}\bigl(y_{\text{pred}}^{(i)}-y_{\text{true}}^{(i)}\bigr)\\[6pt] b \;\leftarrow\; b-\frac{\eta}{|\mathcal B|}\sum_{i\in\mathcal B}\bigl(y_{\text{pred}}^{(i)}-y_{\text{true}}^{(i)}\bigr) \end{cases}} $$
3. 循環多輪 (epochs) 直到收斂或達到迭代上限。

數學分析：拓展

在這一部分，我們主要回答如下幾個問題

1. 為什麼令損失函數的偏導數為 \(0\) 就能求出最優參數？

核心要點

1. 一階必要條件（First-Order Necessary Condition） ：若可微函數在某點取得極值（極小 / 極大 / 鞍點），其梯度必須為零。
2. 充分性通常依賴於目標函數的性質：對 凸 損失而言，任何駐點（梯度為零的點）都是全局最小點；若進一步滿足 Hessian 正定，則最小值唯一。

假設命題：損失函數的偏導數為 \(0\) \(\leftrightarrow\) 參數最優

1.1 一階必要條件 （必要性證明）

由導數的性質（高等數學）可知：若可微函數在某點取得極值（極小 / 極大 / 鞍點），其梯度必須為零。 下給出一個證明：

1.2 為何在凸損失下是充分條件（充分性證明）

（TODO：重寫這一部分）

若 \(L(\theta)\) 為 凸函數（最常見的如線性迴歸的 MSE、Logistic 迴歸的交叉熵），則滿足 $$ L(\lambda\theta_1+(1-\lambda)\theta_2) \;\le\; \lambda L(\theta_1)+ (1-\lambda)L(\theta_2), \quad\forall\;\theta_1,\theta_2,\;\lambda\in[0,1]. $$ 在凸函數上，任何駐點都是全局最小點，因為若存在 \(\theta^*\) 使 \(\nabla L(\theta^*)=0\)，則對任意 \(\theta\) $$ L(\theta)\;\ge\;L(\theta^*) + \nabla L(\theta^*)^{\!\top}(\theta-\theta^*) = L(\theta^*). $$ 這説明 \(\theta^*\) 的目標值不大於任意其他點，即為 全局最優。 進一步，若 Hessian \(\nabla^2 L(\theta)\) 正定，則其駐點 唯一。

1.3 對非凸情形的補充

• 若 \(L\) 非凸（如深度網絡的損失），\(\nabla L=0\) 仍是必要條件，但不保證全局最小，可能落在局部極小或鞍點。
• 此時常藉助二階信息（Hessian 的正定性）或 隨機初始化 + 多次優化 來逃離差的局部解。

2. 為什麼選擇 L2 損失函數作為最小化目標

2.1 L2 損失函數的正確性

在線性迴歸任務中，我們假定真實 \(y\) 與原樣本 \(\mathbf x\) 之間存在線性關係 \(y = \mathbf w^\top \mathbf x + b\)。顯然，如果數據集所採集到的 \(y\) 十分精確，那麼求解 \(\mathbf w\) 向量的任務就轉化為了 \(d+1\) 元一次方程組求解（詳見線性代數：解線性方程組 部分的相關內容）。然而在實際數據集中，我們發現數據集樣本 \(y\) 與 \(\mathbf x\) 之間並沒有嚴格滿足線性關係，這可能是由於以下兩種原因造成的：

1. \(y\) 與 \(\mathbf x\) 之間並非線性關係
2. \(y\) 的採集過程中存在噪聲

在真實數據集中，這兩種原因都有可能存在。然而在使用線性模型擬合的過程中，我們假設 \(y\) 與 \(\mathbf x\) 內部存在一個（近似的）線性關係，因此我們不考慮（1）這一種原因。

注：我們其實是假設 \(y\) 與 \(\mathbf x\) 內部 存在的是嚴格線性關係，但是在實際應用中我們可以 放寬 線性模型的使用限制，只要存在一個 近似 的線性關係，那麼該模型擬合出來的效果便是理想的。

考慮（2），我們假設對於每個樣本，都存在噪聲 \(\varepsilon \sim \mathcal N(0,\sigma^{2})\)，即有

$$ y_{\text{true}} = \mathbf w^\top \mathbf x + b + \varepsilon. $$

其中，我們假定噪聲服從正態分佈，這是由於正態分佈的數理統計性質導致的，詳見 2.2 部分的講解。此外，正態分佈的方差為 0，這是由於我們在訓練過程中，可以使用 偏置項 \(b\) 吸收了噪聲中的方差。

顯然，如果噪聲的均值為 \(\mu \neq 0\)，那麼便意味着最優 \(w^*\) 預測出來的 \(y_{pred}\) 將會與 \(y_{true}\) 系統性的偏移 \(\mu\)。這不是我們想要的。因此，我們可以用 \(b\) 對這一個系統性偏移進行吸收，從而避免這一個系統性的預測偏差

上述包含噪聲的 \(y\) 與 \(X\) 構成了整個數據集 \((X, \mathbf y)\)，其中 \(\mathbf w^*\) 已經是線性模型所希望擬合的最佳參數。

其中，正態分佈 \(\mathcal N(\mu, \sigma^2)\) 的概率密度函數為

$$ p(x) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp\Bigl(-\frac{(x-\mu)^{2}}{2\sigma^{2}}\Bigr). $$

那麼，給定這個數據集，我們應該如何求解最佳參數呢？
我們使用 極大似然估計方法 進行運算（關於 極大似然估計方法 的概念可以參考下面的補充 2.3）。

假設我們得到了最優參數 \(\mathbf w^*\)，那麼我們知道對於每一個樣本點 \(\mathbf x^{(i)}\)，\(\mathbf w^{*\top}\mathbf x^{(i)}\) 的值都是確定的（我們記為 \(y_{\text{pred}}^{*(i)}\)），即

$$ y_{\text{true}}^{(i)} = y_{\text{pred}}^{*(i)} + \varepsilon, $$

即我們知道對於樣本點 \(i\)，其標籤 \(y_{\text{true}}^{(i)}\) 的分佈將服從 \(\mathcal N(y_{\text{pred}}^{*(i)}, \sigma^{2})\)。

依據此，我們現在可以寫出通過給定的 \(\mathbf x\) 觀測到特定 \(y\) 的 似然（likelihood）：

$$ p\bigl(y^{(i)}\mid\mathbf x^{(i)},\mathbf w,b\bigr) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp\Bigl(-\frac{\bigl(y^{(i)}-\mathbf w^\top\mathbf x^{(i)}-b\bigr)^{2}}{2\sigma^{2}}\Bigr) = \mathcal N\bigl(y^{(i)} \mid \mathbf w^\top\mathbf x^{(i)}+b,\, \sigma^{2}\bigr). $$

注：在許多文章中，我們將 notation 簡化為 \(p(y^{(i)}\mid\mathbf x^{(i)})\)。省略了 \(w\) 與 \(b\) 的內容

現在查看這個數據集，整批樣本獨立同分布，故 整體似然 為

$$ P(\mathbf y\mid X,\mathbf w,b) = \prod_{i=1}^{n}p\bigl(y^{(i)}\mid\mathbf x^{(i)},\mathbf w,b\bigr). $$

現在，根據極大似然估計法，參數 \(\mathbf w\) 和 \(b\) 的最優值是使整個數據集的 似然最大 的值，也就是

$$ (\mathbf w^*, b^*) = \arg\max_{\mathbf w,b} P(\mathbf y\mid X,\mathbf w,b). $$

依據極大似然估計法則，我們的目標就是尋找參數 \(w,b\) ，以 最大化 似然 \(P(\mathbf y\mid X,\mathbf w,b)\)，具體操作上，我們通過對參數分別求偏導數為0的方法確保求出的解為極大值，隨後通過極值點唯一的方法證明其是最大值。但指數項累乘很難求導求極大值。因此，一個常見的技巧是我們可以將優化目標改為 最小化負對數似然 \(-\log P(\mathbf y\mid X,\mathbf w,b)\)。

注：對數化似然函數是一個 trick。至於為什麼最小化取負數僅僅是習慣原因。
注2：有些非凸函數可能有不止一個極大似然，因此我們確實無法保證其是最大似然（全局最優），不過一個二階的局部極值有時候在大多數時候是可以接受的。

對數似然為

$$ \log P(\mathbf y\mid X,\mathbf w,b) = \sum_{i=1}^{n}\log p\bigl(y^{(i)}\mid\mathbf x^{(i)},\mathbf w,b\bigr) $$

（注意除了累乘變成累加，內部的每一項也要分別求對數）

因此，我們進一步展開，得到負對數似然

$$ -\log P(\mathbf y\mid X,\mathbf w,b) = \frac{n}{2}\log(2\pi\sigma^{2}) + \frac{1}{2\sigma^{2}}\sum_{i=1}^{n}\bigl(y^{(i)}-\mathbf w^\top\mathbf x^{(i)}-b\bigr)^{2}. $$

我們希望求的參數是 \(\mathbf w, b\)，因此在極大似然法則求偏導數的時候，常數項不會影響極值點的解，我們只需要關注非常數項。

• 第一項 \(\frac{n}{2}\log(2\pi\sigma^{2})\) 不含 \(\mathbf w, b\)，可視為常數。
• 噪聲方差 \(\sigma^2\) 是我們假設的數據集內樣本點分佈的內在屬性，我們不需要估計它，其也不是一個變量，因此可以在公式中完全忽略這一項，將其視為常數 \(1\)。
• \(X\) 和 \(y\) 是從給定數據集中來的變量，就是用來估計參數 \(\mathbf w\) 和 \(b\) 的，因此不能忽略

因此，最大化對數似然等價於最小化

$$ \mathcal L(\mathbf w,b) = \frac{1}{2}\sum_{i=1}^{n}\bigl(y^{(i)}-\mathbf w^\top\mathbf x^{(i)}-b\bigr)^{2} = \frac{1}{2}\lVert X\mathbf w+b\mathbf 1-\mathbf y\rVert_{2}^{2}, $$

這正是 L2 損失。

注： \(\lVert\cdot\rVert_{2}\)表示 二範數（L-2 範數 / Euclidean norm）。給定向量 \(\mathbf v\in\mathbb R^{n}\)，其 2-範數定義為

$$ \lVert \mathbf v\rVert_{2}= \sqrt{\sum_{i=1}^{n} v_{i}^{2}} $$

因此上述表達式可以改寫為求殘差的平方和，也就是：

$$ \bigl\lVert X\mathbf w+b\mathbf 1-\mathbf y\bigr\rVert_{2}^{2} =\Bigl(\sqrt{\sum_{i=1}^{n}\bigl(x_i^{\mathsf T}\mathbf w+b-y_i\bigr)^{2}}\Bigr)^{2} =\sum_{i=1}^{n}\bigl(x_i^{\mathsf T}\mathbf w+b-y_i\bigr)^{2}, $$

因此，在高斯噪聲假設下，最小化 L2 損失給出的解即為線性模型參數的最大似然估計，統計意義上最優。

2.2 補充：為什麼估測噪聲為正態分佈

在實踐中，我們主要基於多種的理由選擇假定噪聲為正態分佈。其中最重要的理論支撐是 中心極限定理 與 最大熵原理

1. 中心極限定理 (Central Limit Theorem)
   實際測量誤差通常由大量獨立的小擾動之和構成；當這些擾動無偏且具有有限方差時，其總和將在樣本量足夠大時趨向正態分佈。
2. 最大熵原理 (Maximum Entropy Principle)
   在僅已知誤差的期望為零、方差為 \(\sigma^{2}\) 的前提下，信息最少（熵最大）的分佈就是高斯分佈。若沒有更多先驗信息，選擇正態噪聲是最不帶偏見也最符合"奧卡姆剃刀"的假設。

3. 數學 良性質（tractability） 與工程可行性

   • 高斯分佈使對數似然轉化為"平方項"，方便求導，梯度與 Hessian 均顯式可得。
   • 由此帶來的 L2 損失是嚴格凸函數，解析解與數值優化算法（SGD、L-BFGS 等）都非常高效。

中心極限定理 非常適用於基於實驗採樣所獲得的數據集。而 最大熵原理 則保證了當我們不知道 \(\varepsilon\) 的真實分佈時，選擇正態噪聲不會引入額外偏差/偏見。

但有時候，我們可能對噪聲分佈存在一定感知（即先驗知識）。例如，我們可能發現數據集噪聲呈長尾或含大量離羣點。在這種情況下，我們完全可以假定數據集噪聲服從其它分佈，並換用其他損失函數（例如更魯棒的 L1 損失或 Huber 損失以替代 L2）。

噪聲分佈與損失函數的對應關係

2.3 極大似然估計介紹

參考資料：
極大似然估計的思想及計算[例題] - hello\_nullptr - 博客園

極大似然估計 (Maximum Likelihood Estimation, MLE) 是一種在統計學中估計模型參數的方法。它的基本思想是：找到一組參數值，使得在這組參數下，觀測到的數據出現的概率（即似然函數）最大。

2. 形式化表述

給定問題：我們假設隨機變量 \(\hat X\) 服從分佈 \(\hat X \,\sim \, p(\theta)\)，其中 \(p(\theta)\) 為某個概率分佈，其控制參數為 \(\theta\)。現在我們有從從這一分佈中抽樣出來的觀測數據 \(X\)。我們希望通過 \(X\) 來估測 \(\theta\) 的真實值。

極大似然估計的思路是尋找一個參數\(\theta\)，使得我們觀測到 \(X\) 的概率最大（也就是最大化 \(P(X\mid\theta)\) ）。在極大似然估計的框架下，上述思路具體的形式化表述為：

定義似然函數 \(L(\theta)\) 是給定參數 \(\theta\) 下觀測數據 \(X\) 的聯合概率分佈函數。其形式為：

$$ L(\theta) = P(X\mid\theta). $$

因此得到最佳估測參數 \(\theta^*\) 滿足：

$$ \theta^* = \arg\max_{\theta} L(\theta) $$

因此，問題轉化為了求解 \(L(\theta)\) 的最大值點。在實踐中，我們經常使用求偏導數的方法獲得極大值點，並通過證明或者近似手段將其視為是最大值點。

特別的，在機器學習領域下， \(X\) 一般包含多個觀測值 \(x_1, x_2, \ldots, x_n\)，並且我們假設觀測是獨立同分布的。因此，我們可以進一步將公式寫為如下形式：

$$ L(\theta) = \prod_{i=1}^{n} p(x_i\mid\theta). $$

其中：

• \(n\) 表示觀測值的個數。
• \(p(x_i\mid\theta)\) 表示給定參數 \(\theta\) 下觀測值為 \(x_i\) 的概率。
• 符號 "\(\prod\)" 表示連乘運算。

3. 極大似然估計的基本步驟

1. 定義似然函數
   根據觀測數據和模型，定義似然函數，即觀測數據在給定參數下的聯合概率密度函數（或聯合概率質量函數）。

2. 求極大值
   通過最大化似然函數（或其對數形式，因為對數函數是單調增函數，不會改變極值點的位置，但可能使計算更方便）來求解參數。

   $$ \theta^* = \arg\max_{\theta} L(\theta) = \arg\max_{\theta} \log L(\theta). $$

3. 求解參數
   對對數似然函數求導，令導數為零，解方程得到參數估計值。

4. 極大似然估計的補充舉例：拋硬幣問題

假設如下場景：
我們拋硬幣 10 次，觀測到 7 次正面，3 次反面。問：抽中紅球和白球的概率最有可能為多少？（最有可能：極大似然最大值）

設正面朝上的概率為 \(p\)，則似然函數為

$$ L(p) = \binom{10}{7} p^{7} (1-p)^{3}. $$

對數似然為

$$ \log L(p) = \log\binom{10}{7} + 7\log p + 3\log(1-p). $$

對 \(p\) 求導並令其為零：

$$ \frac{\mathrm d}{\mathrm dp}\log L(p) = \frac{7}{p} - \frac{3}{1-p} = 0 \quad\Rightarrow\quad p^* = \frac{7}{10} = 0.7. $$

因此，極大似然估計給出的正面概率為 70%。

線性模型代碼實現示例

手敲版本

這裏提供一個基於pytorch的較為簡單的代碼實現（這裏沒有使用自動微分方法，而是手敲了我們求出來的導數函數

# 從數據集中遍歷k個epoch，每個epoch選擇b個樣本（打亂後逐步b個b個選擇），然後求梯度，並優化模型參數
import random
from abc import ABC, abstractmethod
from dataclasses import dataclass

import torch

def synthetic_data(w, b, num_examples):  # @save
    """
    生成y=Xw+b+噪聲
    其中：w (d,); b 標量; num_examples = n
    """
    X = torch.normal(0, 1, size=(num_examples, len(w)))  # 隨機一組(n,d)的數據，分佈為N(0,1)
    epsilon = torch.normal(0, 0.01, size=(num_examples,))
    y = torch.matmul(X, w) + b + epsilon  # (n,)
    y = y.reshape((-1, 1))  # reshape成二維數組(n,1)

    # ============ 數據一致性檢查 ============
    # (1) X 與 y 都應為二維數組
    assert len(X.shape) == 2 and len(y.shape) == 2, \
        f"X 和 y 必須都是二維數組，但當前形狀分別為 {X.shape} 與 {y.shape}"

    # (2) 樣本數檢查
    assert num_examples == X.shape[0] == y.shape[0], \
        f"樣本數不一致：num_examples={num_examples}, X 行={X.shape[0]}, y 行={y.shape[0]}"

    # (3) 特徵維度數檢查
    assert X.shape[1] == w.shape[0], \
        f"特徵維度不匹配：X 列數={X.shape[1]}，而 w 長度={w.shape[0]}"
    return X, y


def load_example_ds() -> tuple[torch.Tensor, torch.Tensor]:
    true_w = torch.tensor([2, -3.4])
    true_b = 4.2
    features, labels = synthetic_data(true_w, true_b, 1000)
    return features, labels


class AbstractDataset(ABC):
    @abstractmethod
    def load(self) -> tuple[torch.Tensor, torch.Tensor]:
        # 返回 X,y
        pass


class DatasetLoader:
    def __init__(self, batch_size: int, dataset: AbstractDataset):
        self.batch_size = batch_size
        self.X, self.y = dataset.load()
        self.__dataset_check(self.X, self.y)

    def __dataset_check(self, X: torch.Tensor, y: torch.Tensor):
        # (1) X 與 y 都應為二維數組
        assert len(X.shape) == 2 and len(y.shape) == 2, \
            f"X 和 y 必須都是二維數組，但當前形狀分別為 {X.shape} 與 {y.shape}"

        # (2) 樣本數檢查
        assert X.shape[0] == y.shape[0], \
            f"樣本數不一致：X 行={X.shape[0]}, y 行={y.shape[0]}"

    def sample(self):
        num_examples = len(self.X)
        indices = list(range(num_examples))
        # 這些樣本是隨機讀取的，沒有特定的順序
        random.shuffle(indices)
        for i in range(0, num_examples, self.batch_size):
            batch_indices = torch.tensor(
                indices[i: min(i + self.batch_size, num_examples)])
            yield self.X[batch_indices], self.y[batch_indices]


class AbstractModel(ABC):
    @abstractmethod
    def forward(self, X: torch.Tensor) -> torch.Tensor:
        pass

    @abstractmethod
    def optimize(self, x: torch.Tensor, y_pred: torch.Tensor, y_true: torch.Tensor, learning_rate: float):
        pass

    @abstractmethod
    def print_params(self):
        pass


class LinearModel(AbstractModel):
    def __init__(self, in_features: int):
        self.w = torch.normal(0, 0.01, size=(in_features, 1), requires_grad=False)
        self.b = torch.zeros(1, requires_grad=False)

    def forward(self, X: torch.Tensor) -> torch.Tensor:
        return X @ self.w + self.b

    def optimize(self, X: torch.Tensor, y_pred: torch.Tensor, y_true: torch.Tensor, learning_rate: float):
        e = y_pred - y_true  # (n,1)
        n = y_true.shape[0]
        grad_w = X.T @ e
        grad_b = e.sum()
        self.w -= learning_rate / n * grad_w
        self.b -= learning_rate / n * grad_b

    def print_params(self):
        print(f"Learned w: {self.w.squeeze().tolist()}")
        print(f"Learned b: {self.b.item()}")


@dataclass
class TrainArgs:
    epoch: int
    batch_size: int
    learning_rate: float
    dataset: AbstractDataset
    model: AbstractModel


class MyDataset(AbstractDataset):
    def load(self) -> tuple[torch.Tensor, torch.Tensor]:
        return load_example_ds()


def train_pipeline(train_args: TrainArgs):
    dataset = train_args.dataset
    dataset_loader = DatasetLoader(train_args.batch_size, dataset)
    model = train_args.model
    for epoch in range(train_args.epoch):
        print(f"\n===== Epoch {epoch + 1}/{train_args.epoch} =====")
        # --------- 訓練 ---------
        for batch_x, batch_y_true in dataset_loader.sample():
            batch_y_pred = model.forward(batch_x)
            model.optimize(batch_x, batch_y_pred, batch_y_true, learning_rate=train_args.learning_rate)
        # --------- 評估 ---------
        print(f"Epoch {epoch} Train Completed! Evaluating...")
        total_se, total_n = 0.0, 0
        with torch.no_grad():
            for bx, by in dataset_loader.sample():
                y_pred = model.forward(bx)
                total_se += ((y_pred - by) ** 2).sum().item()
                total_n += by.shape[0]
        avg_l2 = total_se / total_n
        print(f"Avg L2 loss: {avg_l2:.6f}")

    print("Train completed! Printing Model params:")
    model.print_params()


if __name__ == "__main__":
    train_args = TrainArgs(
        epoch=10,
        batch_size=32,
        learning_rate=0.03,
        dataset=MyDataset(),
        model=LinearModel(in_features=2)
    )
    train_pipeline(train_args)

Pytorch標註寫法

一個更好的調庫寫法

import random
from pathlib import Path
from typing import Tuple

import torch
from torch import nn
from torch.utils.data import Dataset, DataLoader

# ===== 1. 數據集（保持與原接口兼容） =====
# 這裏假設 load_example_ds 返回 (X, y)，且 X,y 均為二維 Tensor
from classes.class3_2.dataset import load_example_ds


class ExampleDataset(Dataset):
    """將現有 load_example_ds() 封裝為標準 Dataset"""

    def __init__(self) -> None:
        X, y = load_example_ds()  # X:(N, in_features), y:(N, 1)
        assert X.ndim == 2 and y.ndim == 2, "Expect 2-D tensors"
        assert X.shape[0] == y.shape[0], "Mismatched sample size"
        self.X, self.y = X.float(), y.float()  # 確保 dtype = float32

    def __len__(self) -> int:
        return self.X.shape[0]

    def __getitem__(self, idx: int) -> Tuple[torch.Tensor, torch.Tensor]:
        return self.X[idx], self.y[idx]


# ===== 2. 線性模型 + 損失函數 + 優化器 =====
def build_model(in_features: int, lr: float = 0.03) -> tuple[nn.Module, torch.optim.Optimizer, nn.Module]:
    model = nn.Linear(in_features, 1)  # bias=True 默認即含 b
    optimizer = torch.optim.SGD(model.parameters(), lr=lr)
    criterion = nn.MSELoss()
    return model, optimizer, criterion


# ===== 3. 訓練與評估 =====
def train(
    model: nn.Module,
    optimizer: torch.optim.Optimizer,
    criterion: nn.Module,
    dataloader: DataLoader,
    epochs: int = 10,
    device: torch.device | str = "cpu",
) -> None:
    device = torch.device(device)
    model.to(device)

    for epoch in range(1, epochs + 1):
        # ---- Train ----
        model.train()
        for X_batch, y_batch in dataloader:
            X_batch, y_batch = X_batch.to(device), y_batch.to(device)

            optimizer.zero_grad()
            y_pred = model(X_batch)
            loss = criterion(y_pred, y_batch)
            loss.backward()
            optimizer.step()

        # ---- Evaluate ----
        model.eval()
        with torch.no_grad():
            se_sum, n_total = 0.0, 0
            for X_batch, y_batch in dataloader:
                X_batch, y_batch = X_batch.to(device), y_batch.to(device)
                y_pred = model(X_batch)
                se_sum += ((y_pred - y_batch) ** 2).sum().item()
                n_total += y_batch.shape[0]
            avg_mse = se_sum / n_total

        print(f"Epoch {epoch:02d}/{epochs} | Avg MSE: {avg_mse:.6f}")

    # ---- Done ----
    w, b = model.weight.data.squeeze(), model.bias.data.item()
    print("\nTraining finished. Learned parameters:")
    print(f"w: {w.tolist()}")
    print(f"b: {b:.6f}")


# ===== 4. main 入口 =====
if __name__ == "__main__":
    torch.manual_seed(42)        # 為可重複性設隨機種子
    random.seed(42)

    batch_size = 32
    epochs = 10
    lr = 0.03

    dataset = ExampleDataset()
    dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

    in_features = dataset.X.shape[1]
    model, optimizer, criterion = build_model(in_features, lr=lr)

    train(model, optimizer, criterion, dataloader, epochs=epochs)