很多剛入行甚至想入行數據分析的朋友,往往會陷入一個誤區:以為數據分析就是不停地做報表、畫餅圖。
其實,數據分析的核心魅力在於 “推斷”——即見微知著。
在現實生活中,我們很難獲取“全量數據”(比如你不可能調查全國每一個人的身高),那麼,如何通過手中的“小樣本”去推測“大總體”的規律?
這就需要用到統計學中的推斷分析。
本文將結合代碼來介紹推斷分析中最常用的三大方法:參數估計、假設檢驗、非參數檢驗。
1. 參數估計
想象你在煮一鍋排骨湯。你想知道湯鹹不鹹,你不會把整鍋湯都喝完,而是舀起一勺嘗一嘗。
- 那一勺湯就是樣本。
- 那一勺的鹹度就是樣本統計量。
- 整鍋湯的鹹度就是我們要猜的總體參數。
參數估計就是:根據樣本的特徵(比如樣本均值),去估計總體的特徵(比如總體均值)。
它通常分為兩種:
- 點估計:直接説“這鍋湯是1.5%的鹽度”。(但這很容易被打臉,因為太絕對)
- 區間估計:説“這鍋湯的鹽度在1.4%到1.6%之間,我有95%的把握”。(這就是置信區間,更科學)
區間估計是最常使用的方式,下面通過一個示例來演示參數估計的具體使用。
import numpy as np
from scipy import stats
# 1. 模擬數據
np.random.seed(42)
true_mean = 15 # 上帝視角的真實均值
sample_salaries = np.random.normal(loc=true_mean, scale=3, size=100) # 模擬100個樣本
# 2. 計算統計量
sample_mean = np.mean(sample_salaries)
sample_std = np.std(sample_salaries, ddof=1)
n = len(sample_salaries)
# 計算95%置信區間
# 這裏的 scale 使用的是標準誤 (Standard Error) = 樣本標準差 / sqrt(n)
conf_int = stats.t.interval(
confidence=0.95, df=n - 1, loc=sample_mean, scale=sample_std / np.sqrt(n)
)
lower_bound, upper_bound = conf_int
print(f"樣本均值: {sample_mean:.2f}k")
print(f"95%置信區間: [{lower_bound:.2f}k, {upper_bound:.2f}k]")
# 運行結果:
'''
樣本均值: 14.69k
95%置信區間: [14.15k, 15.23k]
'''
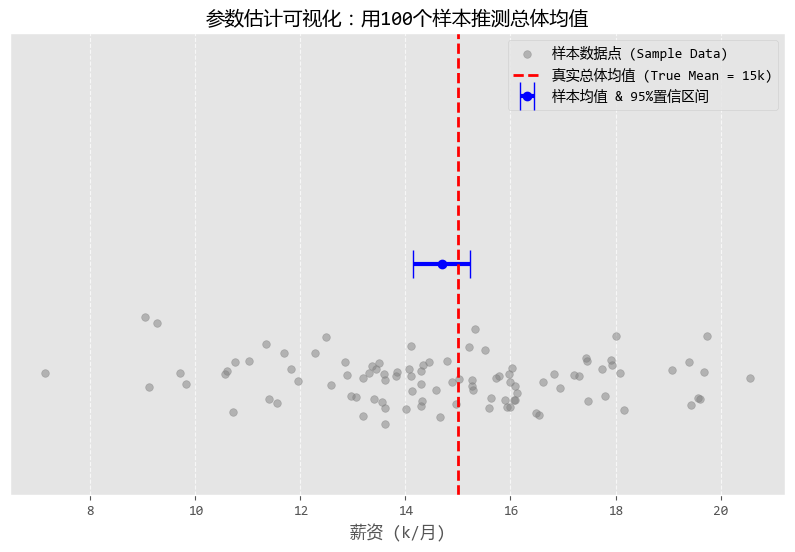
圖形化之後的結果如下:
從圖中可以看出:
- 灰色的散點:是你調研的那100個數據分析師的工資。你會發現有的高有的低,散落在各地。
- 藍色的點和橫線:
- 藍點是你算出來的樣本均值(約14.67k),雖然不完全等於真實的15k,但很接近。
- 藍色的橫線就是置信區間。它的含義是:“雖然我不知道確切數字,但我敢打賭,真實數字就在這根藍線的範圍內。”
- 紅色的虛線:這是真實的總體均值(15k)。
- 結論:你可以清楚地看到,紅色的虛線確實穿過了藍色的橫線。恭喜你!這次“參數估計”成功捕獲了真理!
數據分析不是算命,算出來的不是一個死的數字,而是一個科學的範圍。
我們就是用參數估計的方法,在不確定性中尋找確定性。
2. 假設檢驗
假設檢驗是數據分析中最常用的決策工具。它的邏輯是:先立一個Flag(假設),然後看證據(數據)是否打臉。
- 原假設 :通常代表“無事發生”、“沒有變化”、“運氣好”。
- 備擇假設:通常代表“有事發生”、“真的有效果”。
- P值:表示原假設成立時,出現當前數據的概率。P值越小,説明原假設越不靠譜(通常以0.05為界限)。
下面通過一個電商APP的A/B測試場景,來演示假設檢驗的使用。
假設某電商APP想把 “購買” 按鈕從 藍色 改成 紅色 。
- 原假設:紅色按鈕和藍色按鈕的轉化率沒區別(差別純屬偶然)。
- 備擇假設:紅色按鈕的轉化率顯著高於藍色按鈕。
我們採集了兩組用户的消費金額數據來進行T檢驗。
# 1. 模擬AB測試數據
# 藍色按鈕組(對照組):平均消費 100元
group_blue = np.random.normal(loc=100, scale=20, size=1000)
# 紅色按鈕組(實驗組):平均消費 105元 (我們要檢驗這個提升是否顯著)
group_red = np.random.normal(loc=105, scale=25, size=1000)
# 2. 進行獨立樣本T檢驗 (T-test)
t_stat, p_val = stats.ttest_ind(group_blue, group_red)
print(f"P值: {p_val:.5f}")
# 3. 判斷結論
alpha = 0.05
if p_val < alpha:
print("結論:拒絕原假設。紅色按鈕帶來的消費提升是【統計顯著】的,建議全量上線!")
else:
print("結論:無法拒絕原假設。兩組差異可能是誤差導致的,建議維持原狀。")
# 運行結果:
'''
P值: 0.00000
結論:拒絕原假設。紅色按鈕帶來的消費提升是【統計顯著】的,建議全量上線!
'''
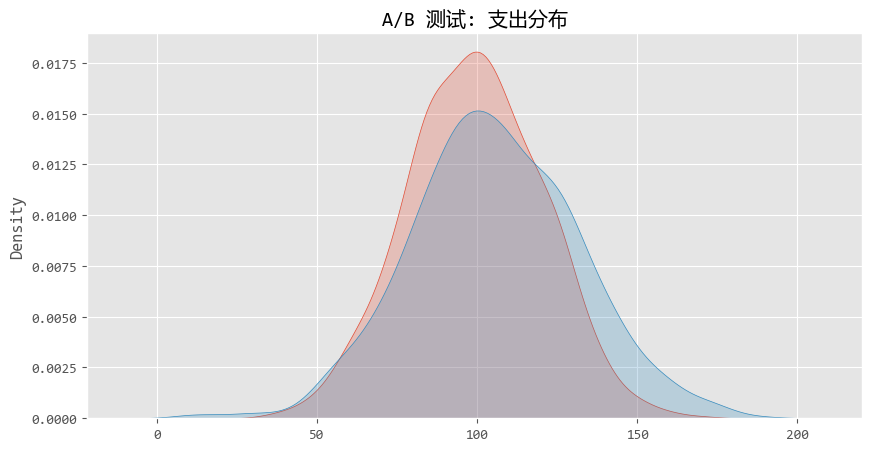
圖形化結果如下:
從圖中,我們可以看出,兩條曲線(紅色和藍色)其實重疊度很高。
對於新手,看到這個圖,可能會陷入一個誤區,覺得“這兩座山峯看起來差不多嘛,沒啥區別”。
但在統計學上,兩座山峯的 “重心” (均值)發生了 顯著偏移 。這就是假設檢驗的威力--在重疊的噪聲中識別出偏移的信號。
3. 非參數估計
前面的 “參數估計” 和 “T檢驗” 都有一個嬌氣的脾氣:它們通常假設數據是服從 “正態分佈” 的(也就是漂亮的鐘形曲線)。
但在現實生活中,很多數據並不正態,或者數據甚至是定序的(比如:非常滿意、滿意、一般、不滿意)。
這時候,傳統的 T檢驗 就失效了,我們需要請出 非參數檢驗 。
它不依賴數據的分佈形狀,非常抗造。
假設我們要對比兩款手遊《王者榮耀》和《原神》玩家每天的遊玩時長。
由於《原神》玩家可能存在大量的“長尾”用户(玩特別久),數據往往是嚴重右偏的,不符合正態分佈。
這時候對比兩組數據差異,就不能用T檢驗,我們使用非參數估計中的一種方式:曼-惠特尼U檢驗 (Mann-Whitney U test)。
# 1. 模擬非正態分佈數據 (使用指數分佈模擬由偏數據)
# 遊戲A:平均時長較短
game_a_hours = np.random.exponential(scale=1.0, size=100)
# 遊戲B:平均時長較長
game_b_hours = np.random.exponential(scale=1.5, size=100)
# 2. 首先,檢查一下正態性 (Shapiro-Wilk檢驗)
# 如果P < 0.05,説明不是正態分佈
_, p_norm_a = stats.shapiro(game_a_hours)
print(f"遊戲A正態性檢驗P值: {p_norm_a:.4f} (小於0.05則非正態)")
# 3. 使用非參數檢驗:Mann-Whitney U檢驗
# 它可以比較兩個獨立樣本的分佈是否存在差異(側重於中位數/秩次的比較)
u_stat, p_val_nonparam = stats.mannwhitneyu(game_a_hours, game_b_hours, alternative='two-sided')
print(f"Mann-Whitney U檢驗 P值: {p_val_nonparam:.5f}")
if p_val_nonparam < 0.05:
print("結論:兩款遊戲的玩家遊玩時長分佈存在顯著差異。")
else:
print("結論:兩款遊戲玩家遊玩時長無顯著差異。")
# 運行結果:
'''
遊戲A正態性檢驗P值: 0.0000 (小於0.05則非正態)
Mann-Whitney U檢驗 P值: 0.00003
結論:兩款遊戲的玩家遊玩時長分佈存在顯著差異。
'''
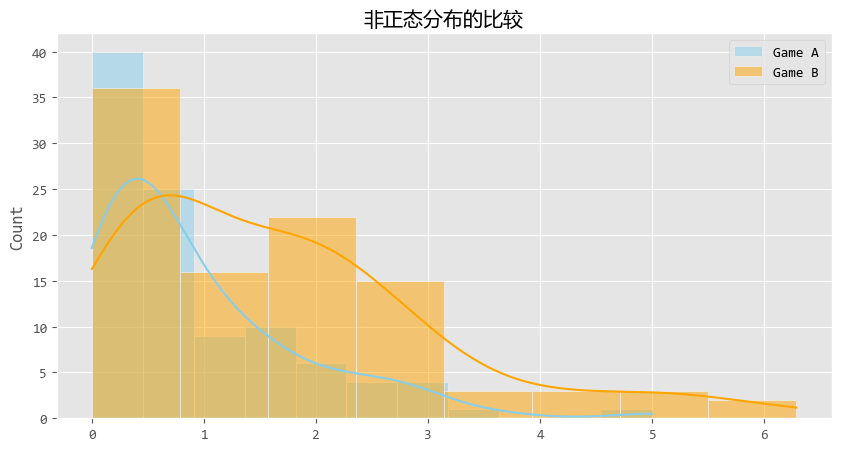
可視化結果如下:
儘管數據長得歪瓜裂棗(嚴重右偏),U檢驗依然穩健地告訴我們:這兩組數據不一樣。
U檢驗比較的不僅僅是平均值,它更多是在比較 “秩次”(Ranking)。
通俗點説,它發現如果我們把兩組玩家混在一起排名,Game B的玩家即使不看具體時長,排名也普遍比Game A的玩家靠前。
從圖中來看,你會看到橙色(Game B)的尾巴明顯比藍色(Game A)拖得更長、更厚實。
這説明Game B(比如《原神》)更容易讓玩家沉浸更久,或者擁有更多的重度玩家。
4. 總結
恭喜你!你已經掌握了數據推斷分析的核心邏輯:
- 參數估計:當你只有樣本,想知道總體的數值範圍時使用。(比如估算平均薪資)
- 假設檢驗:當你數據比較“完美”(正態分佈),想判斷差異是不是真的時使用。(比如A/B測試)
- 非參數檢驗:當你數據分佈奇怪、或者只有排名/等級數據時使用。(比如評分對比、長尾數據分析)
這三板斧是數據分析師行走江湖的必備技能。掌握了它們,你就不僅僅是一個“做表的”,而是一個能從數據中挖掘真相的“偵探”!