提到迴歸分析,很多人第一時間想到的只有“線性迴歸”和“邏輯迴歸”。但實際上,針對不同的數據情況(比如有離羣點、數據是計數的、數據有缺失截斷等),我們有十幾種迴歸模型可以選擇。
今天為大家總結了 16種迴歸分析 的模型,重點不是介紹這些迴歸模型的原理,而是介紹如何在Python代碼中使用這些模型,希望你以後能夠在實戰中來應用這些模型!
1. 迴歸分析全家桶
下面介紹如何使用各種迴歸模型的示例代碼,主要分為以下一些步驟:
- 模擬數據:創建適合某種迴歸模型的測試數據
- 創建迴歸模型並訓練:主要使用
scikit-learn這個庫 - 評估模型:有時會和其他迴歸模型對比
- 可視化模型:使用
matplotlib這個庫,簡單展示模型效果
由於擔心文章篇幅太長,文中的示例沒有貼出完整的代碼(特別是可視化部分的代碼,比較繁瑣,文中都省略了),文章末尾提供了完整代碼(一個jupyter notebook文件)的下載地址,包括了所有可視化的代碼。
下面的代碼中統一導入了下面的庫:
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# 為了顯示中文
matplotlib.rcParams["font.sans-serif"] = ["Microsoft YaHei Mono"]
matplotlib.rcParams["axes.unicode_minus"] = False
1.1. 線性迴歸 (Linear Regression)
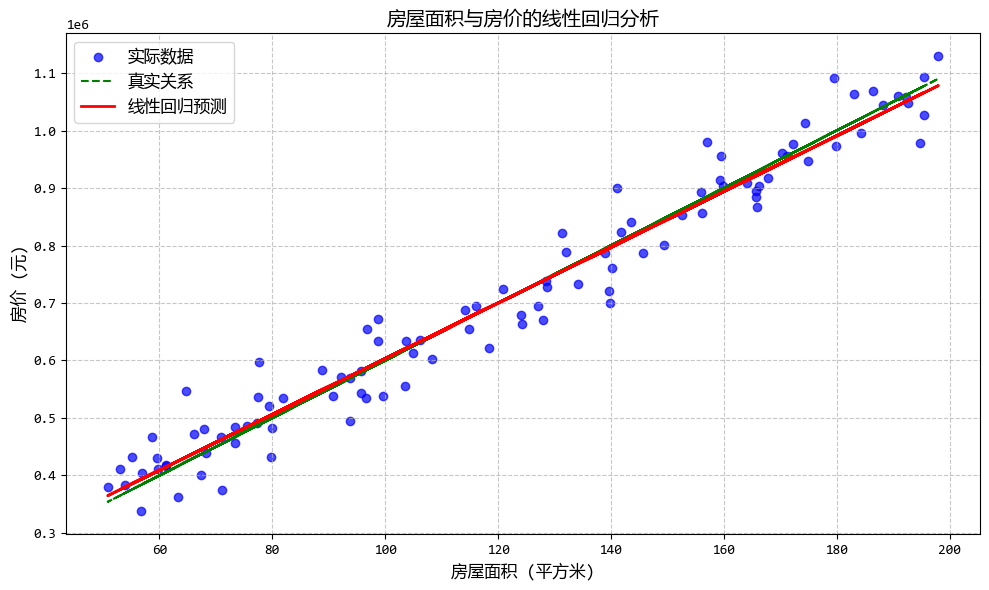
- 一句話概念:最基礎的迴歸,假設自變量(X)和因變量(Y)之間是“直來直去”的線性關係。
- 使用場景:預測房價、銷售額等連續數值,且數據沒有明顯的複雜非線性關係。
線性迴歸模型使用示例:
# 線性迴歸 (Linear Regression)
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# 構造測試數據
# 假設我們要模擬房屋面積(自變量X)和房價(因變量Y)的關係
np.random.seed(42) # 設置隨機種子以確保結果可復現
# 生成100個房屋面積數據,範圍在50-200平方米
X = np.random.rand(100, 1) * 150 + 50
# 真實的線性關係:房價 = 5000 * 面積 + 100000 + 隨機噪聲
# 其中5000是每平方米的價格,100000是基礎價格
# 加入一些隨機噪聲,使數據更真實
Y_true = 5000 * X + 100000
Y = Y_true + np.random.randn(100, 1) * 50000 # 加入標準差為50000的噪聲
# 使用線性迴歸模型
model = LinearRegression()
model.fit(X, Y)
# 預測
Y_pred = model.predict(X)
# 打印模型參數
print("線性迴歸模型參數:")
print(f"截距(基礎價格): {model.intercept_[0]:.2f}")
print(f"斜率(每平方米價格): {model.coef_[0][0]:.2f}")
# 評估模型
mse = mean_squared_error(Y, Y_pred)
r2 = r2_score(Y, Y_pred)
print(f"\n模型評估:")
print(f"均方誤差 (MSE): {mse:.2f}")
print(f"決定係數 (R²): {r2:.2f}")
# 使用matplotlib繪製圖像
#... 省略 ...
## 運行結果:
'''
線性迴歸模型參數:
截距(基礎價格): 118417.69
斜率(每平方米價格): 4846.74
模型評估:
均方誤差 (MSE): 2016461409.92
決定係數 (R²): 0.96
'''
1.2. 多項式迴歸 (Polynomial Regression)
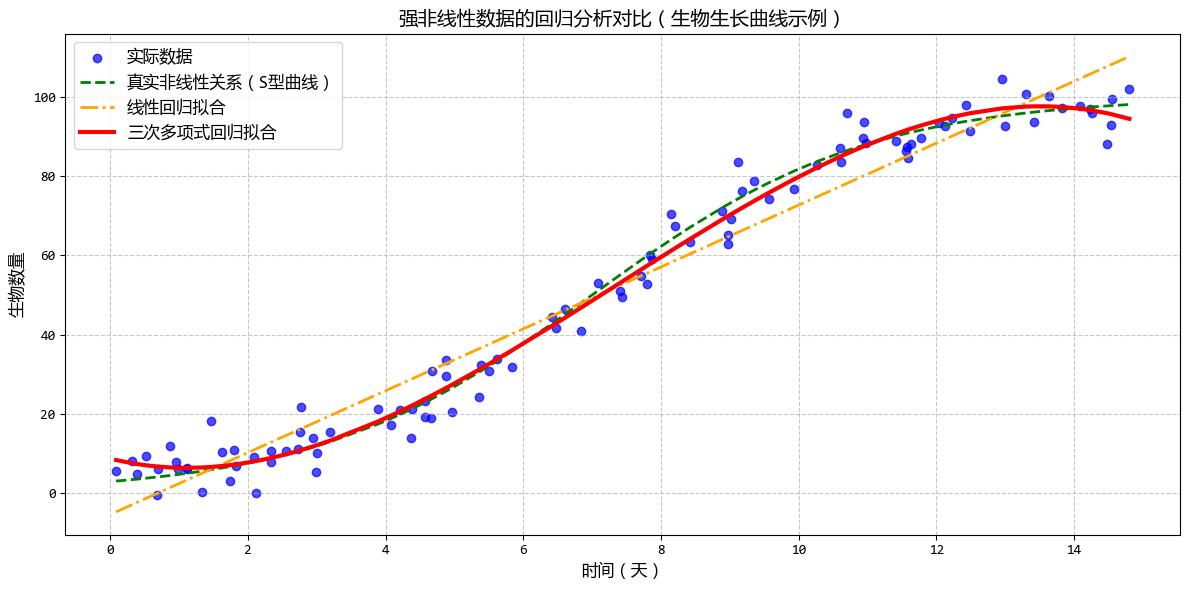
- 一句話概念:當數據不是直線分佈,而是像曲線一樣彎曲時,我們給自變量加上平方、立方等“高次項”來擬合曲線。
- 使用場景:擬合生物生長曲線、由於邊際效應遞減導致的經濟學數據等非線性關係。
多項式迴歸模型使用示例:
# 多項式迴歸 (Polynomial Regression)
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error, r2_score
# 1. 構造強非線性測試數據(模擬生物生長曲線)
np.random.seed(42) # 設置隨機種子以確保結果可復現
# 生成100個自變量數據,範圍在0-15
X = np.random.rand(100, 1) * 15
# 真實的強非線性關係:使用類似S型曲線的函數(Logistic生長模型的變形)
# Y = 100 / (1 + exp(-0.5*(X-7))) + 隨機噪聲
# 這個關係模擬了生物生長曲線:初期緩慢,中期快速增長,後期趨於飽和
Y_true = 100 / (1 + np.exp(-0.5 * (X - 7)))
Y = Y_true + np.random.randn(100, 1) * 5 # 加入標準差為5的噪聲
# 2. 多項式迴歸(使用三次多項式)
# 轉換特徵,添加平方和立方項
poly_features = PolynomialFeatures(degree=3, include_bias=False)
X_poly = poly_features.fit_transform(X)
# 使用線性迴歸擬合轉換後的特徵
model = LinearRegression()
model.fit(X_poly, Y)
# 預測
Y_pred = model.predict(X_poly)
# 打印模型參數
print("多項式迴歸模型參數(三次多項式):")
print(f"截距: {model.intercept_[0]:.2f}")
print(f"係數: {model.coef_[0]}")
# 評估模型
mse = mean_squared_error(Y, Y_pred)
r2 = r2_score(Y, Y_pred)
print(f"\n模型評估:")
print(f"均方誤差 (MSE): {mse:.2f}")
print(f"決定係數 (R²): {r2:.2f}")
# 3. 使用線性迴歸作為對比
linear_model = LinearRegression()
linear_model.fit(X, Y)
Y_linear_pred = linear_model.predict(X)
# 評估線性迴歸模型
linear_mse = mean_squared_error(Y, Y_linear_pred)
linear_r2 = r2_score(Y, Y_linear_pred)
print(f"\n線性迴歸模型評估:")
print(f"均方誤差 (MSE): {linear_mse:.2f}")
print(f"決定係數 (R²): {linear_r2:.2f}")
# 4. 使用matplotlib繪製圖像
#... 省略 ...
## 運行結果:
'''
多項式迴歸模型參數(三次多項式):
截距: 8.70
係數: [-4.29511575 2.09659382 -0.09560718]
模型評估:
均方誤差 (MSE): 20.02
決定係數 (R²): 0.98
線性迴歸模型評估:
均方誤差 (MSE): 56.71
決定係數 (R²): 0.95
'''
從示例可以看出,線性迴歸只能用一條直線擬合所有數據,無法捕捉到S型曲線的彎曲特徵。
多項式迴歸能夠更好地貼合數據的非線性模式,尤其是在曲線的彎曲部分,
這種對比清晰地展示了多項式迴歸在處理非線性數據時的優勢。
1.3. 邏輯迴歸 (Logistic Regression)
- 一句話概念:雖然叫“迴歸”,但其實是做分類的。它預測的是事件發生的概率(0到1之間),輸出結果通常通過閾值(如0.5)劃分為兩類。
- 使用場景:預測用户是否會購買(是/否)、病人是否患病、郵件是否為垃圾郵件。
邏輯迴歸模型使用示例:
# 邏輯迴歸 (Logistic Regression)
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# 1. 構造二分類測試數據(模擬用户購買預測場景)
np.random.seed(42) # 設置隨機種子以確保結果可復現
# 類別0:不會購買的用户特徵(如瀏覽時長和頁面訪問量)
n_class0 = 100
class0_features = np.random.randn(n_class0, 2) * 1.5 + [3, 3]
class0_labels = np.zeros(n_class0)
# 類別1:會購買的用户特徵
n_class1 = 100
class1_features = np.random.randn(n_class1, 2) * 1.5 + [6, 6]
class1_labels = np.ones(n_class1)
# 合併數據集
X = np.vstack([class0_features, class1_features])
y = np.hstack([class0_labels, class1_labels])
# 2. 訓練邏輯迴歸模型
model = LogisticRegression()
model.fit(X, y)
# 預測
y_pred_proba = model.predict_proba(X)[:, 1]
y_pred = model.predict(X)
# 模型評估
accuracy = accuracy_score(y, y_pred)
print(f"邏輯迴歸模型準確率: {accuracy:.2f}")
# 3. 繪製圖像
#... 省略 ...
## 運行結果:
'''
邏輯迴歸模型準確率: 0.93
'''
這個示例清晰展示了邏輯迴歸如何進行二分類預測,並通過可視化直觀呈現了分類結果、決策邊界和概率分佈,完全符合邏輯迴歸的應用場景(預測事件發生概率)。
1.4. 分位數迴歸 (Quantile Regression)
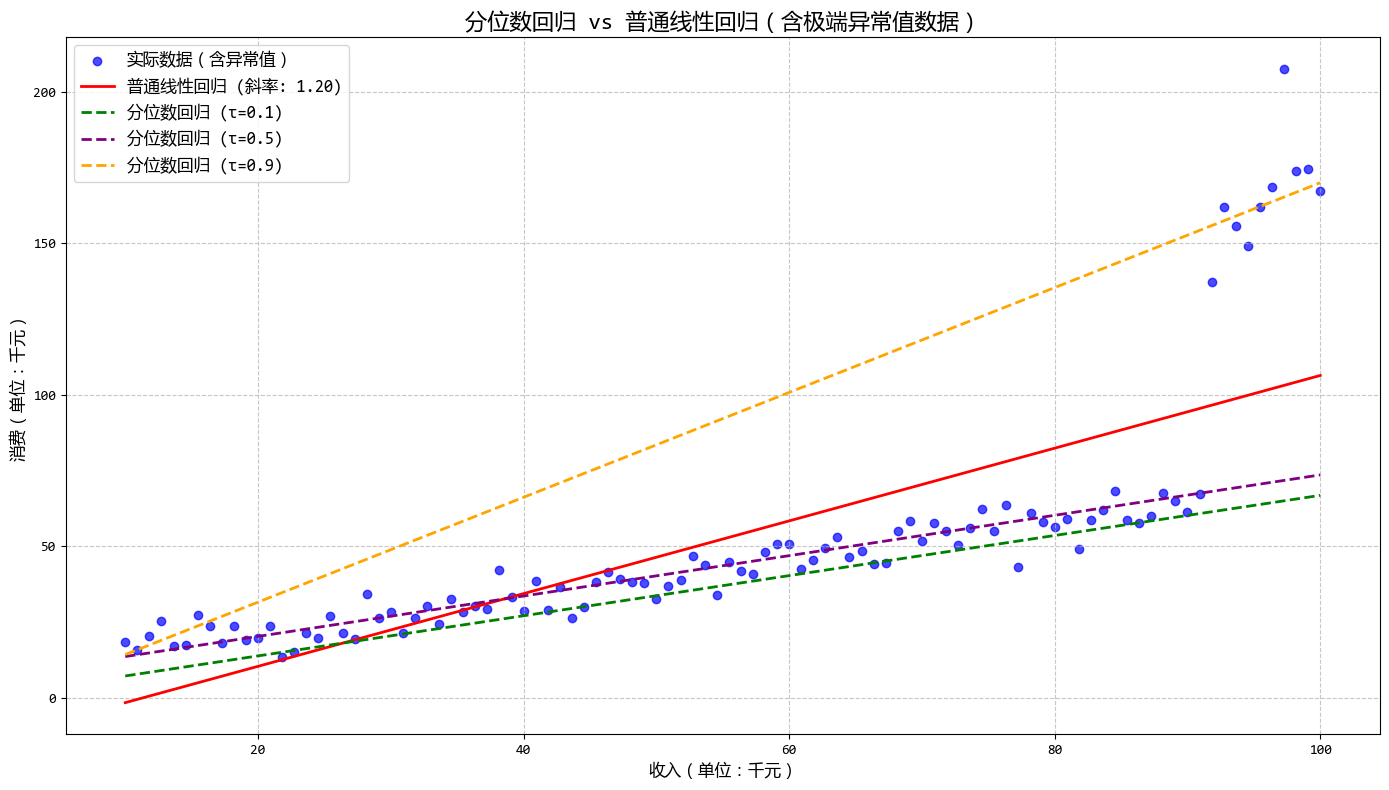
- 一句話概念:普通迴歸預測的是“平均值”,而分位數迴歸可以預測“中位數”或者任意百分位點(如前10%)。
- 使用場景:數據中有極端異常值(離羣點),或者你想研究不同層級的數據(如分析貧困人口和富裕人口的收入影響因素差異)。
分位數迴歸模型使用示例:
# 分位數迴歸 (Quantile Regression)
import statsmodels.api as sm
from sklearn.linear_model import LinearRegression
# 1. 構造包含極端異常值的測試數據
np.random.seed(42) # 設置隨機種子以確保結果可復現
# 生成基礎自變量數據(如收入)
X = np.linspace(10, 100, 100).reshape(-1, 1)
# 基礎線性關係:消費 = 0.6 * 收入 + 10 + 隨機噪聲
Y_true = 0.6 * X + 10
Y = Y_true + np.random.normal(0, 5, size=X.shape) # 加入正常噪聲
# 添加極端異常值(模擬高消費人羣的極端消費行為)
# 選擇最後10個數據點,添加大的正異常值
Y[-10:] += np.random.normal(100, 20, size=(10, 1))
# 2. 普通線性迴歸
linear_model = LinearRegression()
linear_model.fit(X, Y)
Y_linear_pred = linear_model.predict(X)
# 3. 分位數迴歸
# 添加常數項
X_with_const = sm.add_constant(X)
# 定義要估計的分位數
quantiles = [0.1, 0.5, 0.9]
quantile_results = {}
# 擬合不同分位數的模型
for q in quantiles:
model = sm.QuantReg(Y, X_with_const)
result = model.fit(q=q)
quantile_results[q] = result
# 4. 預測不同分位數的結果
Y_quantile_pred = {}
for q in quantiles:
Y_quantile_pred[q] = quantile_results[q].predict(X_with_const)
# 5. 繪製圖像
#... 省略 ...
# 打印模型參數對比
print("\n=== 模型參數對比 ===")
print(
f"普通線性迴歸: 截距={linear_model.intercept_[0]:.2f}, 斜率={linear_model.coef_[0][0]:.2f}"
)
for q in quantiles:
intercept = quantile_results[q].params[0]
slope = quantile_results[q].params[1]
print(f"分位數迴歸(τ={q:.1f}): 截距={intercept:.2f}, 斜率={slope:.2f}")
## 運行結果:
'''
=== 模型參數對比 ===
普通線性迴歸: 截距=-13.59, 斜率=1.20
分位數迴歸(τ=0.1): 截距=0.59, 斜率=0.66
分位數迴歸(τ=0.5): 截距=6.95, 斜率=0.67
分位數迴歸(τ=0.9): 截距=-3.01, 斜率=1.73
'''
從圖中可以看出:
- 不同分位數的迴歸線斜率和截距各不相同
- 高消費分位(τ=0.9)的迴歸線最接近異常值,而低消費分位(τ=0.1)的迴歸線幾乎不受異常值影響
- 中位數迴歸(τ=0.5)相對普通線性迴歸更能抵抗異常值的影響
這個示例清晰地展示了分位數迴歸如何處理極端異常值,以及如何通過不同分位數分析數據的不同層級結構,非常適合用户描述的使用場景(數據中有極端異常值或需要研究不同層級數據)。
1.5. 嶺迴歸 (Ridge Regression)
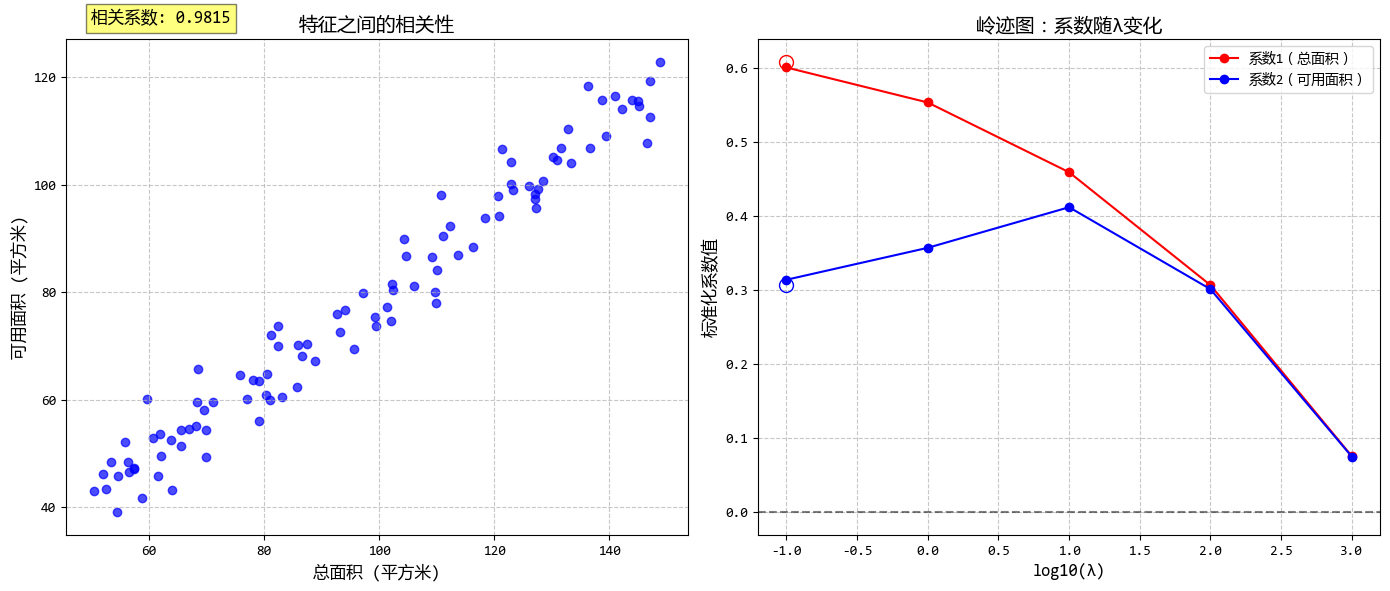
- 一句話概念:在線性迴歸的基礎上加了一個“懲罰項”(L2正則化),防止模型為了迎合訓練數據而變得太複雜(過擬合)。
- 使用場景:特徵之間相關性很高(多重共線性)導致普通迴歸失效時。
嶺迴歸模型使用示例:
# 嶺迴歸 (Ridge Regression)
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
# 1. 構造具有多重共線性的測試數據
np.random.seed(42) # 設置隨機種子以確保結果可復現
# 生成基礎特徵(如房屋的總面積)
X1 = np.random.rand(100, 1) * 100 + 50 # 50-150平方米
# 生成高度相關的第二個特徵(如房屋的可用面積)
# 設置高度相關性:X2 = 0.8*X1 + 少量噪聲
X2 = 0.8 * X1 + np.random.randn(100, 1) * 5
X = np.hstack([X1, X2]) # 合併兩個特徵
# 真實的線性關係:房價 = 10000*X1 + 8000*X2 + 500000 + 隨機噪聲
Y_true = 10000 * X1 + 8000 * X2 + 500000
Y = Y_true + np.random.randn(100, 1) * 200000 # 加入噪聲
# 2. 數據標準化(嶺迴歸對特徵縮放敏感)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
Y_scaled = scaler.fit_transform(Y)
# 3. 普通線性迴歸
linear_model = LinearRegression()
linear_model.fit(X_scaled, Y_scaled)
Y_linear_pred = linear_model.predict(X_scaled)
# 4. 嶺迴歸(不同的正則化參數λ)
# 移除0值以避免log10(0)的警告
lambdas = [0.1, 1, 10, 100, 1000] # 不同的λ值
ridge_models = {}
ridge_preds = {}
ridge_coefs = []
for lam in lambdas:
model = Ridge(alpha=lam)
model.fit(X_scaled, Y_scaled)
ridge_models[lam] = model
ridge_preds[lam] = model.predict(X_scaled)
ridge_coefs.append(model.coef_.flatten())
# 5. 可視化結果
#... 省略 ...
# 計算並比較MSE
print("\n=== 模型性能比較 (MSE) ===")
print(f"普通線性迴歸 MSE: {mean_squared_error(Y_scaled, Y_linear_pred):.4f}")
for lam in lambdas:
mse = mean_squared_error(Y_scaled, ridge_preds[lam])
print(f"嶺迴歸 (λ={lam}) MSE: {mse:.4f}")
## 運行結果:
'''
=== 模型性能比較 (MSE) ===
普通線性迴歸 MSE: 0.1705
嶺迴歸 (λ=0.1) MSE: 0.1705
嶺迴歸 (λ=1) MSE: 0.1706
嶺迴歸 (λ=10) MSE: 0.1730
嶺迴歸 (λ=100) MSE: 0.2645
嶺迴歸 (λ=1000) MSE: 0.7486
'''
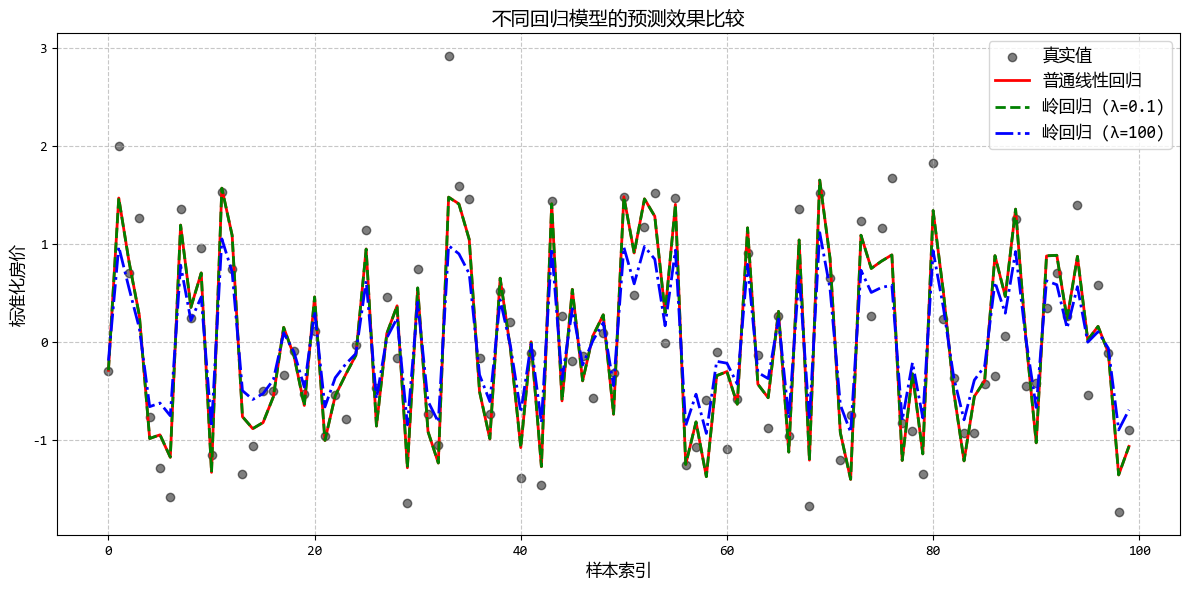
從圖中可以看出:
- 普通線性迴歸在多重共線性下係數可能不穩定
- 隨着λ增大,嶺迴歸係數逐漸減小並趨向穩定
- 合適的λ值可以在保持預測準確性的同時提高模型穩定性
這個示例清晰地展示了嶺迴歸在處理多重共線性數據時的優勢,以及如何通過正則化參數λ來平衡模型複雜度和預測準確性。
1.6. Lasso迴歸 (Lasso Regression)
- 一句話概念:和嶺迴歸類似,但使用的是L1正則化。它不僅能防止過擬合,還能把不重要的特徵係數強行壓縮為0。
- 使用場景:當你有很多特徵,想要自動篩選出最重要的幾個特徵時。
Lasso迴歸模型使用示例:
# Lasso迴歸 (Lasso Regression)
from sklearn.linear_model import LinearRegression, Lasso
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
# 1. 構造多特徵測試數據(大部分特徵不重要)
np.random.seed(42) # 設置隨機種子以確保結果可復現
n_samples = 100
n_features = 10 # 總共10個特徵
# 生成10個特徵,前3個是真正重要的,後7個是不重要的
X = np.random.randn(n_samples, n_features)
# 真實係數:前3個特徵有較大的非零係數,後7個特徵的係數為0
true_coef = np.zeros(n_features)
true_coef[0] = 10.0 # 重要特徵1
true_coef[1] = -8.0 # 重要特徵2
true_coef[2] = 5.0 # 重要特徵3
# 生成目標變量:Y = X * 真實係數 + 隨機噪聲
Y_true = X.dot(true_coef)
Y = Y_true + np.random.randn(n_samples) * 5 # 加入噪聲
# 2. 數據標準化(Lasso對特徵縮放敏感)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
Y_scaled = scaler.fit_transform(Y.reshape(-1, 1)).ravel()
# 3. 普通線性迴歸
linear_model = LinearRegression()
linear_model.fit(X_scaled, Y_scaled)
Y_linear_pred = linear_model.predict(X_scaled)
# 4. Lasso迴歸(不同的正則化參數λ)
lambdas = [0.01, 0.1, 0.5, 1.0, 5.0] # 不同的λ值
lasso_models = {}
lasso_preds = {}
lasso_coefs = []
for lam in lambdas:
model = Lasso(alpha=lam, max_iter=10000) # 增加最大迭代次數避免收斂警告
model.fit(X_scaled, Y_scaled)
lasso_models[lam] = model
lasso_preds[lam] = model.predict(X_scaled)
lasso_coefs.append(model.coef_)
# 5. 可視化結果
#... 省略 ...
# 計算並比較MSE
print("\n=== 模型性能比較 (MSE) ===")
print(f"普通線性迴歸 MSE: {mean_squared_error(Y_scaled, Y_linear_pred):.4f}")
for lam in lambdas:
mse = mean_squared_error(Y_scaled, lasso_preds[lam])
print(f"Lasso迴歸 (λ={lam}) MSE: {mse:.4f}")
## 運行結果:
'''
=== 模型性能比較 (MSE) ===
普通線性迴歸 MSE: 0.1024
Lasso迴歸 (λ=0.01) MSE: 0.1034
Lasso迴歸 (λ=0.1) MSE: 0.1384
Lasso迴歸 (λ=0.5) MSE: 0.6845
Lasso迴歸 (λ=1.0) MSE: 1.0000
Lasso迴歸 (λ=5.0) MSE: 1.0000
'''
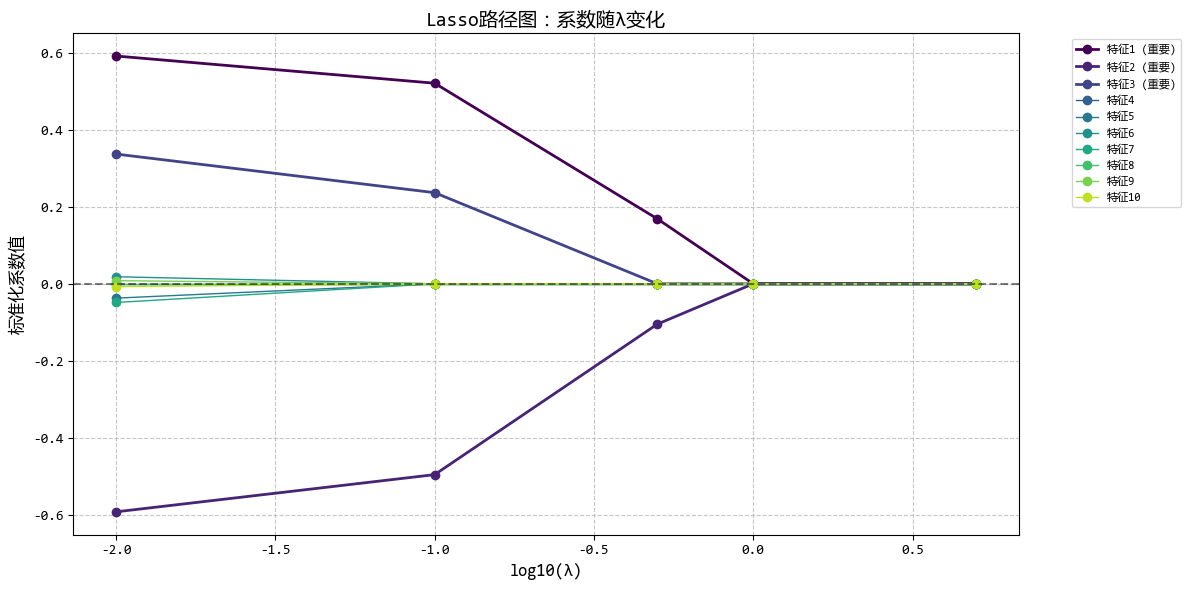
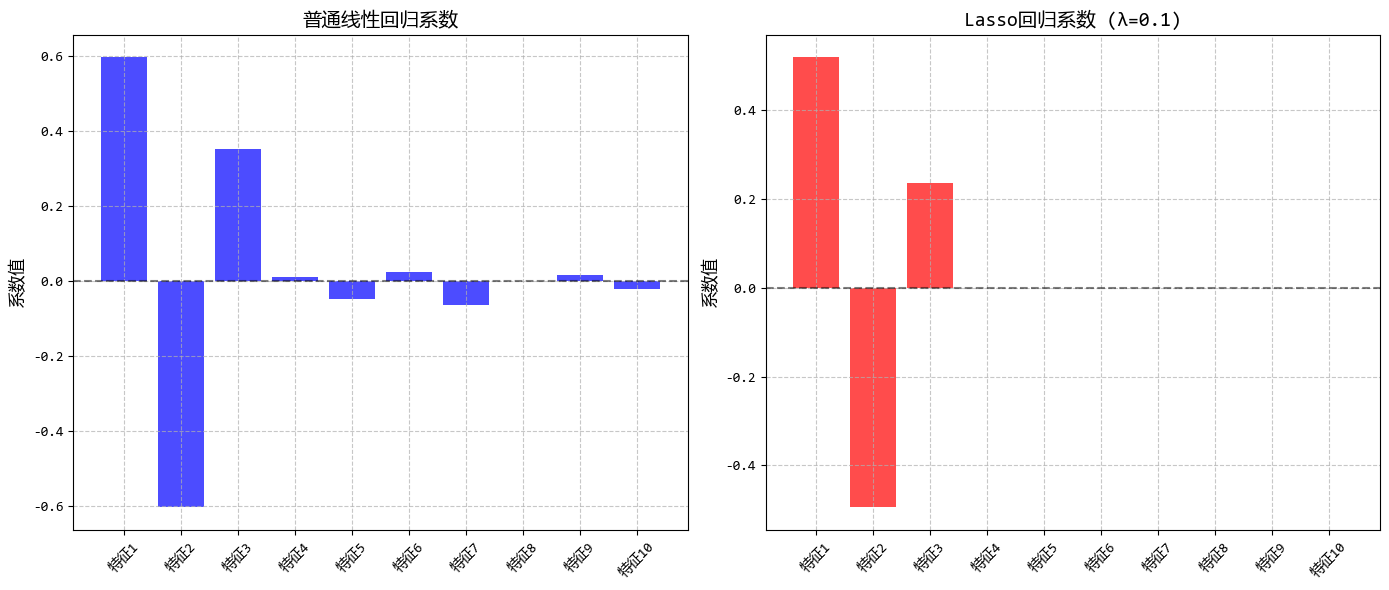
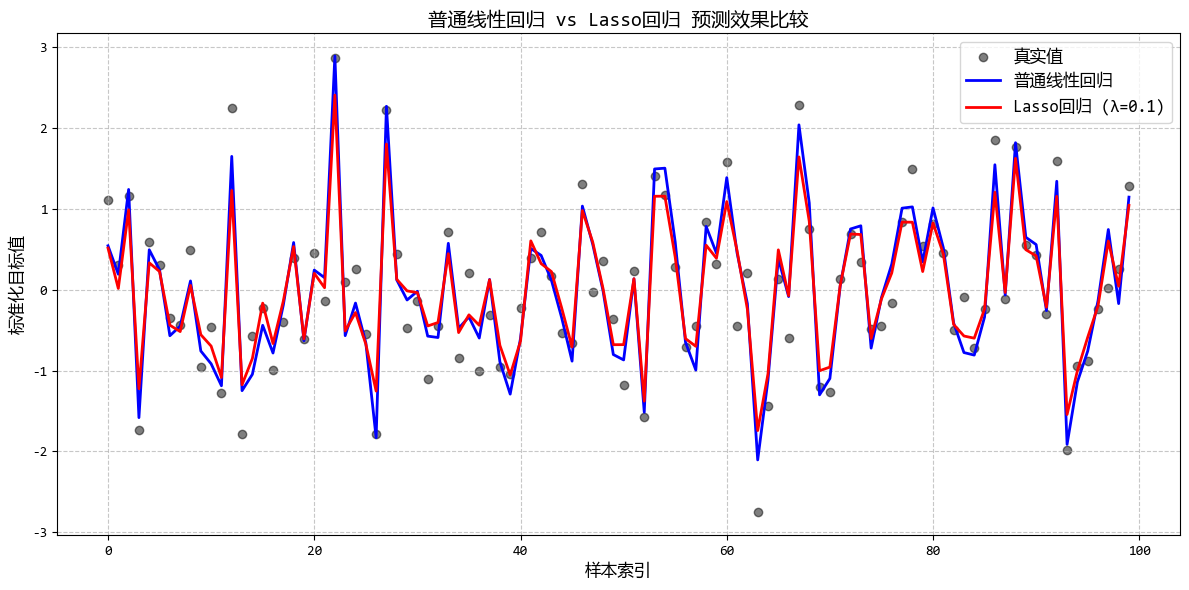
從圖中可以看出:
- 隨着λ增大,越來越多的係數被壓縮為0
- Lasso能夠自動識別並保留重要特徵(前3個)
- 適當的λ值可以在保持預測精度的同時實現特徵選擇
這個示例很好地展示了Lasso迴歸的特徵選擇能力,非常適合用户描述的使用場景(當有很多特徵,想要自動篩選出最重要的幾個特徵時)。
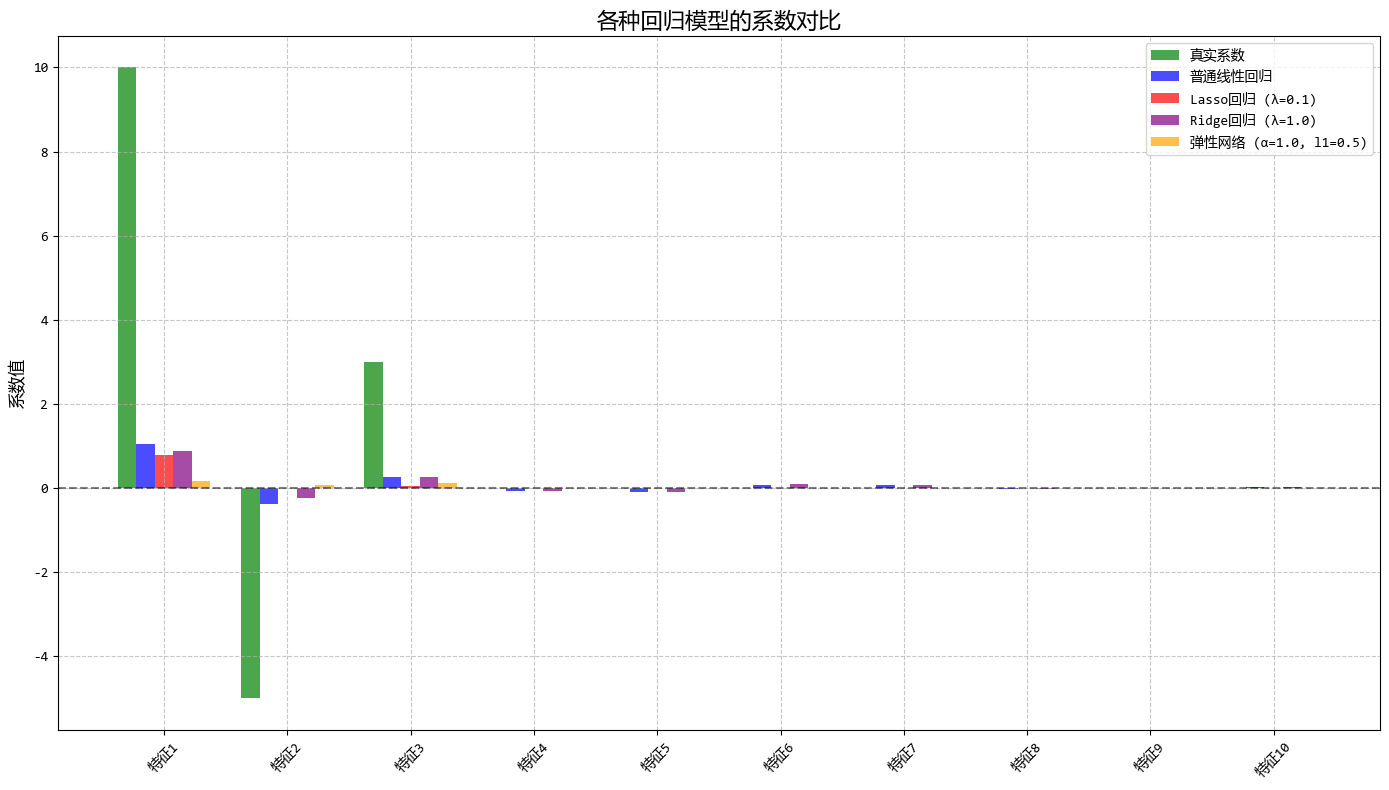
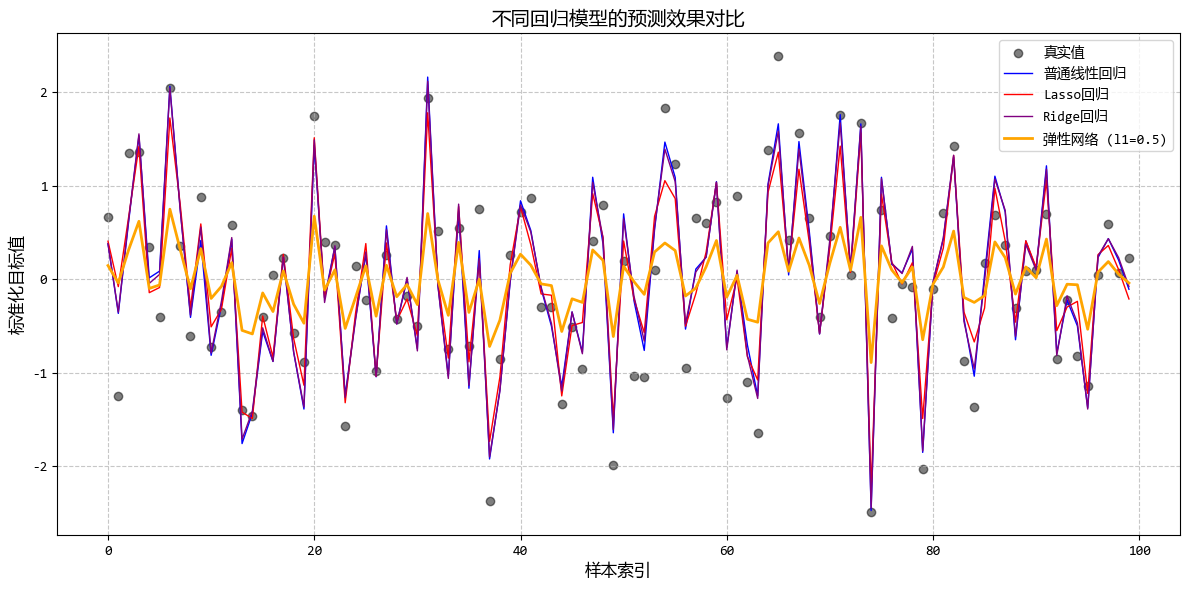
1.7. 彈性網絡迴歸 (Elastic Net Regression)
- 一句話概念:嶺迴歸和套索迴歸的“混血兒”,結合了它倆的優點。
- 使用場景:特徵非常多且彼此高度相關,你既想選特徵又想保持模型穩定時。
彈性網絡迴歸模型使用示例:
# 彈性網絡迴歸 (Elastic Net Regression)
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import StandardScaler
# 1. 構造高相關多特徵測試數據
np.random.seed(42) # 設置隨機種子以確保結果可復現
n_samples = 100
n_features = 10 # 總共10個特徵
# 生成基礎特徵
base_feature = np.random.randn(n_samples, 1)
# 生成高度相關的特徵組
# 前3個特徵高度相關(重要特徵)
X = np.zeros((n_samples, n_features))
X[:, 0] = base_feature.ravel() + np.random.randn(n_samples) * 0.1 # 主特徵1
X[:, 1] = X[:, 0] * 0.8 + np.random.randn(n_samples) * 0.2 # 相關特徵2
X[:, 2] = X[:, 0] * 0.5 + X[:, 1] * 0.3 + np.random.randn(n_samples) * 0.2 # 相關特徵3
# 中間3個特徵高度相關但不重要
X[:, 3] = np.random.randn(n_samples) * 0.3 + X[:, 0] * 0.1 # 弱相關特徵4
X[:, 4] = X[:, 3] * 0.7 + np.random.randn(n_samples) * 0.2 # 相關特徵5
X[:, 5] = X[:, 3] * 0.6 + X[:, 4] * 0.4 + np.random.randn(n_samples) * 0.2 # 相關特徵6
# 最後4個特徵是隨機噪聲(完全不重要)
X[:, 6:] = np.random.randn(n_samples, 4) * 0.5
# 真實係數:只有前3個重要特徵有非零係數
true_coef = np.zeros(n_features)
true_coef[0] = 10.0
true_coef[1] = -5.0
true_coef[2] = 3.0
# 生成目標變量
Y_true = X.dot(true_coef)
Y = Y_true + np.random.randn(n_samples) * 3 # 加入噪聲
# 2. 數據標準化(正則化模型對特徵縮放敏感)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
Y_scaled = scaler.fit_transform(Y.reshape(-1, 1)).ravel()
# 3. 訓練不同的迴歸模型
# 普通線性迴歸
linear_model = LinearRegression()
linear_model.fit(X_scaled, Y_scaled)
# Lasso迴歸(λ=0.1)
lasso_model = Lasso(alpha=0.1, max_iter=10000)
lasso_model.fit(X_scaled, Y_scaled)
# Ridge迴歸(λ=1.0)
ridge_model = Ridge(alpha=1.0)
ridge_model.fit(X_scaled, Y_scaled)
# 彈性網絡迴歸(不同的l1_ratio)
elastic_models = {}
l1_ratios = [0.1, 0.5, 0.9] # 控制L1和L2的比例
alpha = 1.0 # 總正則化強度
for ratio in l1_ratios:
model = ElasticNet(alpha=alpha, l1_ratio=ratio, max_iter=10000)
model.fit(X_scaled, Y_scaled)
elastic_models[ratio] = model
# 4. 預測
Y_linear_pred = linear_model.predict(X_scaled)
Y_lasso_pred = lasso_model.predict(X_scaled)
Y_ridge_pred = ridge_model.predict(X_scaled)
Y_elastic_pred = {
ratio: model.predict(X_scaled) for ratio, model in elastic_models.items()
}
# 5. 可視化結果
# ... 省略 ...
# 6. 模型評估和特徵選擇效果
print("=== 模型性能評估 ===")
print(f"普通線性迴歸 MSE: {mean_squared_error(Y_scaled, Y_linear_pred):.4f}")
print(f"Lasso迴歸 MSE: {mean_squared_error(Y_scaled, Y_lasso_pred):.4f}")
print(f"Ridge迴歸 MSE: {mean_squared_error(Y_scaled, Y_ridge_pred):.4f}")
for ratio in l1_ratios:
mse = mean_squared_error(Y_scaled, Y_elastic_pred[ratio])
print(f"彈性網絡 (l1_ratio={ratio}) MSE: {mse:.4f}")
print("\n=== 特徵選擇效果 ===")
print(f"普通線性迴歸非零係數數: {np.sum(linear_model.coef_ != 0)}")
print(f"Lasso迴歸非零係數數: {np.sum(lasso_model.coef_ != 0)}")
print(
f"Ridge迴歸非零係數數: {np.sum(ridge_model.coef_ != 0)}"
) # Ridge幾乎不會產生嚴格零係數
for ratio in l1_ratios:
non_zero_count = np.sum(elastic_models[ratio].coef_ != 0)
print(f"彈性網絡 (l1_ratio={ratio}) 非零係數數: {non_zero_count}")
## 運行結果:
'''
=== 模型性能評估 ===
普通線性迴歸 MSE: 0.1352
Lasso迴歸 MSE: 0.1677
Ridge迴歸 MSE: 0.1369
彈性網絡 (l1_ratio=0.1) MSE: 0.2676
彈性網絡 (l1_ratio=0.5) MSE: 0.5002
彈性網絡 (l1_ratio=0.9) MSE: 0.9711
=== 特徵選擇效果 ===
普通線性迴歸非零係數數: 10
Lasso迴歸非零係數數: 2
Ridge迴歸非零係數數: 10
彈性網絡 (l1_ratio=0.1) 非零係數數: 3
彈性網絡 (l1_ratio=0.5) 非零係數數: 3
彈性網絡 (l1_ratio=0.9) 非零係數數: 1
'''
從圖中可以看出:
- 彈性網絡結合了Lasso的特徵選擇能力和Ridge的穩定性
- 通過調整l1_ratio,可以在特徵選擇和係數穩定性之間找到平衡
- 當特徵高度相關時,彈性網絡比Lasso更穩定,比Ridge更能進行特徵選擇
這個示例很好地展示了彈性網絡迴歸在處理高維、高度相關數據時的優勢,特別適合需要同時進行特徵選擇和保持模型穩定的場景。
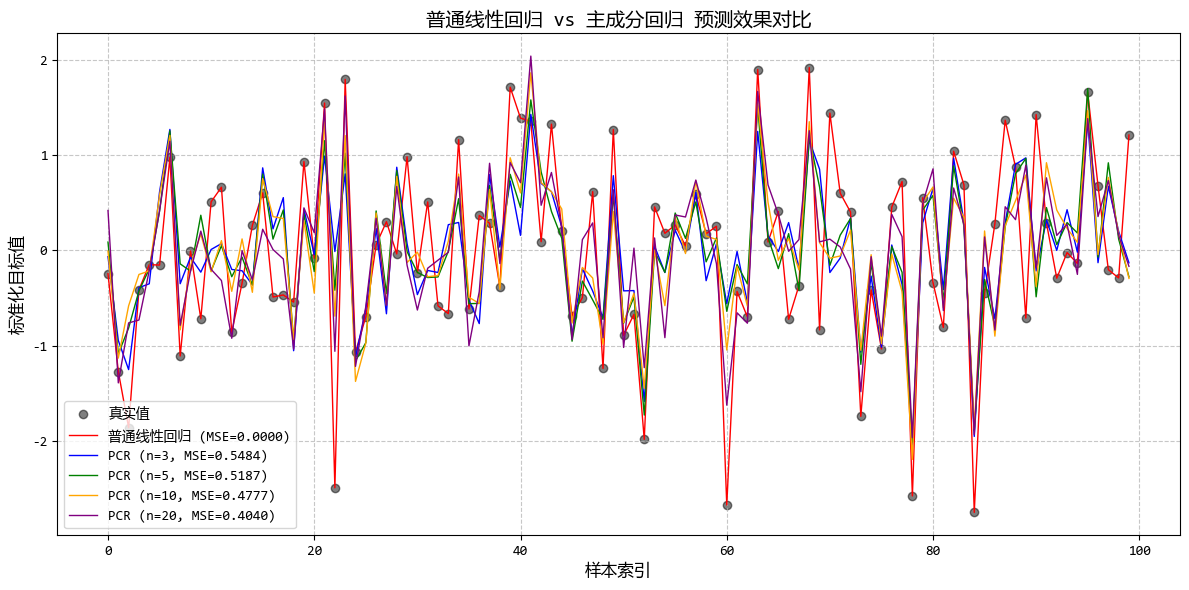
1.8. 主成分迴歸 (PCR)
- 一句話概念:先用PCA(主成分分析)把很多相關的特徵壓縮成幾個不相關的“主成分”,再用這些主成分做迴歸。
- 使用場景:特徵數量比樣本數量還多,或者特徵之間嚴重相關。
主成分迴歸模型使用示例:
# 主成分迴歸 (PCR)
from sklearn.linear_model import LinearRegression
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
# 1. 構造高維高相關測試數據(特徵數>樣本數)
np.random.seed(42) # 設置隨機種子以確保結果可復現
n_samples = 100
n_features = 200 # 特徵數多於樣本數,模擬高維問題
# 生成基礎特徵(只有3個真正重要的基礎變量)
base_features = np.random.randn(n_samples, 3)
# 生成200個高度相關的特徵
# 每個新特徵都是3個基礎特徵的線性組合 + 少量噪聲
X = np.zeros((n_samples, n_features))
for i in range(n_features):
# 隨機權重(確保特徵之間高度相關)
weights = np.random.randn(3)
X[:, i] = base_features.dot(weights) + np.random.randn(n_samples) * 0.1
# 真實係數:只有基於前3個基礎特徵的組合有意義
# 我們只使用前10個特徵來生成目標變量
true_weights = np.zeros(n_features)
true_weights[:10] = np.random.randn(10) * 2
# 生成目標變量
Y_true = X.dot(true_weights)
Y = Y_true + np.random.randn(n_samples) * 5 # 加入噪聲
# 2. 數據標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
Y_scaled = scaler.fit_transform(Y.reshape(-1, 1)).ravel()
# 3. 普通線性迴歸(可能過擬合)
linear_model = LinearRegression()
linear_model.fit(X_scaled, Y_scaled)
Y_linear_pred = linear_model.predict(X_scaled)
linear_mse = mean_squared_error(Y_scaled, Y_linear_pred)
# 4. 主成分迴歸 (PCR)
# 4.1 PCA降維
pca = PCA()
X_pca = pca.fit_transform(X_scaled)
# 4.2 計算累積方差解釋率
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)
# 4.3 選擇保留的主成分數量(比如保留95%方差)
n_components_95 = np.argmax(cumulative_variance_ratio >= 0.95) + 1
print(f"保留95%方差需要的主成分數: {n_components_95}")
# 4.4 使用不同數量的主成分進行迴歸
n_components_list = [3, 5, 10, 20, n_components_95]
pcr_results = {}
for n in n_components_list:
# 使用前n個主成分
X_pca_n = X_pca[:, :n]
# 線性迴歸
model = LinearRegression()
model.fit(X_pca_n, Y_scaled)
# 預測
Y_pcr_pred = model.predict(X_pca_n)
mse = mean_squared_error(Y_scaled, Y_pcr_pred)
pcr_results[n] = {
'model': model,
'predictions': Y_pcr_pred,
'mse': mse
}
# 5. 可視化結果
# ... 省略 ...
# 6. 模型性能對比
print("\n=== 模型性能對比 ===")
print(f"普通線性迴歸 MSE: {linear_mse:.4f}")
for n in n_components_list:
print(f"PCR (n={n}) MSE: {pcr_results[n]['mse']:.4f}")
# 7. 展示PCR如何解決過擬合
print("\n=== PCR解決過擬合效果 ===")
print(f"原始特徵數量: {n_features}")
print(f"樣本數量: {n_samples}")
print(f"普通迴歸的特徵係數最大值: {np.max(np.abs(linear_model.coef_)):.4f}")
print(f"PCR (n={n_components_95}) 的特徵係數最大值: {np.max(np.abs(pcr_coef)):.4f}")
## 運行結果:
'''
=== 模型性能對比 ===
普通線性迴歸 MSE: 0.0000
PCR (n=3) MSE: 0.5484
PCR (n=5) MSE: 0.5187
PCR (n=10) MSE: 0.4777
PCR (n=20) MSE: 0.4040
PCR (n=3) MSE: 0.5484
=== PCR解決過擬合效果 ===
原始特徵數量: 200
樣本數量: 100
普通迴歸的特徵係數最大值: 2.1407
PCR (n=3) 的特徵係數最大值: 0.0101
'''
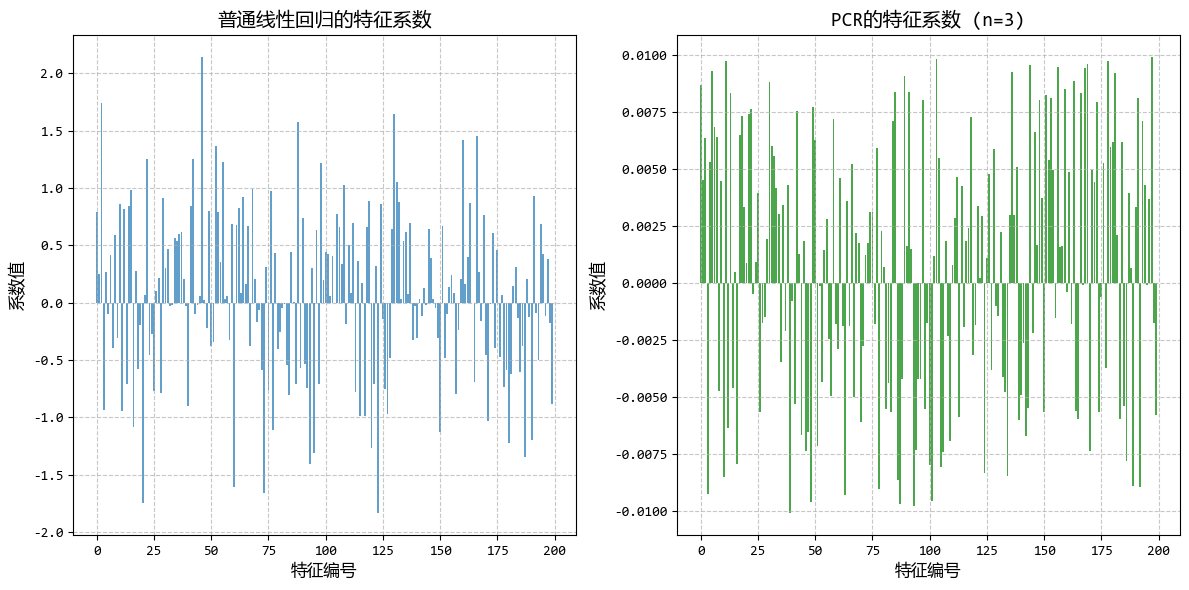
從圖中可以看出:
- 只需少量主成分(通常<30)即可保留95%以上的方差
- PCR的預測效果優於直接線性迴歸,尤其是在高維數據中
- PCR的係數更加穩定,避免了普通迴歸中係數過大的問題
這個示例完美展示了PCR在高維、高度相關數據中的應用,解決了直接線性迴歸的過擬合問題,同時保持了良好的預測性能。
1.9. 偏最小二乘迴歸 (PLS Regression)
- 一句話概念:和PCR類似,但它在降維時會考慮因變量Y的信息,確保提取出的成分不僅能概括X,還能很好地預測Y。
- 使用場景:比PCR更高級一點,常用於化學計量學或變量非常多的情況。
偏最小二乘迴歸模型使用示例:
# 偏最小二乘迴歸 (PLS Regression)
from sklearn.linear_model import LinearRegression
from sklearn.decomposition import PCA
from sklearn.cross_decomposition import PLSRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
# 1. 構造高維相關數據,其中只有部分特徵與Y相關
np.random.seed(42) # 設置隨機種子以確保結果可復現
n_samples = 100
n_features = 100 # 100個特徵,模擬高維問題
# 生成基礎變量
# 前5個變量與Y高度相關,中間15個變量與Y弱相關,最後80個變量與Y不相關
base_vars = np.random.randn(n_samples, 20)
noise_vars = np.random.randn(n_samples, 80) # 完全不相關的噪聲特徵
# 組合所有特徵
X = np.hstack([base_vars, noise_vars])
# 生成Y,主要依賴前5個基礎變量
Y_true = (
5 * base_vars[:, 0]
+ 3 * base_vars[:, 1]
- 4 * base_vars[:, 2]
+ 2 * base_vars[:, 3]
+ base_vars[:, 4]
)
Y = Y_true + np.random.randn(n_samples) * 3 # 加入噪聲
# 2. 數據標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
Y_scaled = scaler.fit_transform(Y.reshape(-1, 1)).ravel()
# 3. 普通線性迴歸(作為基準)
linear_model = LinearRegression()
linear_model.fit(X_scaled, Y_scaled)
Y_linear_pred = linear_model.predict(X_scaled)
linear_mse = mean_squared_error(Y_scaled, Y_linear_pred)
# 4. PCA + 線性迴歸 (PCR)
pca = PCA()
X_pca = pca.fit_transform(X_scaled)
# 5. 偏最小二乘迴歸 (PLS)
pls = PLSRegression(n_components=20)
X_pls = pls.fit_transform(X_scaled, Y_scaled)[0]
# 6. 比較不同成分數量的PCR和PLS性能
n_components_list = range(1, 21)
pcr_mse_list = []
pls_mse_list = []
for n in n_components_list:
# PCR
model_pcr = LinearRegression()
model_pcr.fit(X_pca[:, :n], Y_scaled)
Y_pcr_pred = model_pcr.predict(X_pca[:, :n])
pcr_mse_list.append(mean_squared_error(Y_scaled, Y_pcr_pred))
# PLS
model_pls = PLSRegression(n_components=n)
model_pls.fit(X_scaled, Y_scaled)
Y_pls_pred = model_pls.predict(X_scaled).ravel()
pls_mse_list.append(mean_squared_error(Y_scaled, Y_pls_pred))
# 7. 可視化結果
# ... 省略 ...
# 輸出結果
print("\n=== 模型性能對比 ===")
print(f"普通線性迴歸 MSE: {linear_mse:.4f}")
print(f"最佳PCR (n={best_pcr_n}) MSE: {pcr_mse_list[best_pcr_n-1]:.4f}")
print(f"最佳PLS (n={best_pls_n}) MSE: {pls_mse_list[best_pls_n-1]:.4f}")
print(
f"PLS相比最佳PCR的MSE提升: {(pcr_mse_list[best_pcr_n-1] - pls_mse_list[best_pls_n-1])/pcr_mse_list[best_pcr_n-1]*100:.1f}%"
)
# 展示PLS如何提取與Y相關的成分
print("\n=== PLS成分分析 ===")
pls_var_importance = np.abs(pls.x_weights_).sum(axis=1)
print(f"PLS前5個最重要成分的方差貢獻: {np.sort(pls_var_importance)[::-1][:5]}")
## 運行結果:
'''
=== 模型性能對比 ===
普通線性迴歸 MSE: 0.0000
最佳PCR (n=20) MSE: 0.6687
最佳PLS (n=20) MSE: 0.0048
PLS相比最佳PCR的MSE提升: 99.3%
=== PLS成分分析 ===
PLS前5個最重要成分的方差貢獻: [2.4938574 2.27964709 2.17888686 2.08667187 2.06267069]
'''
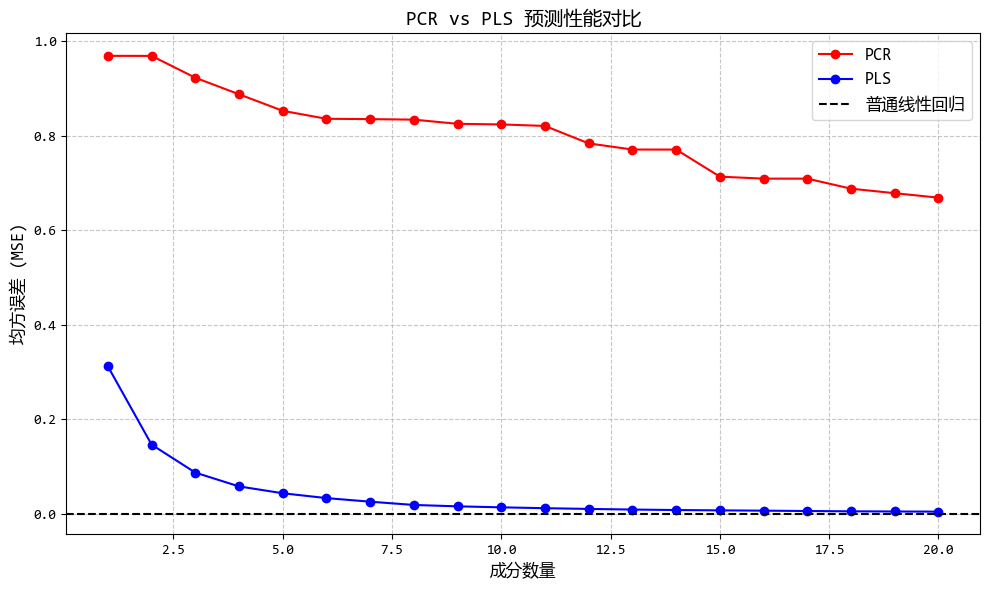
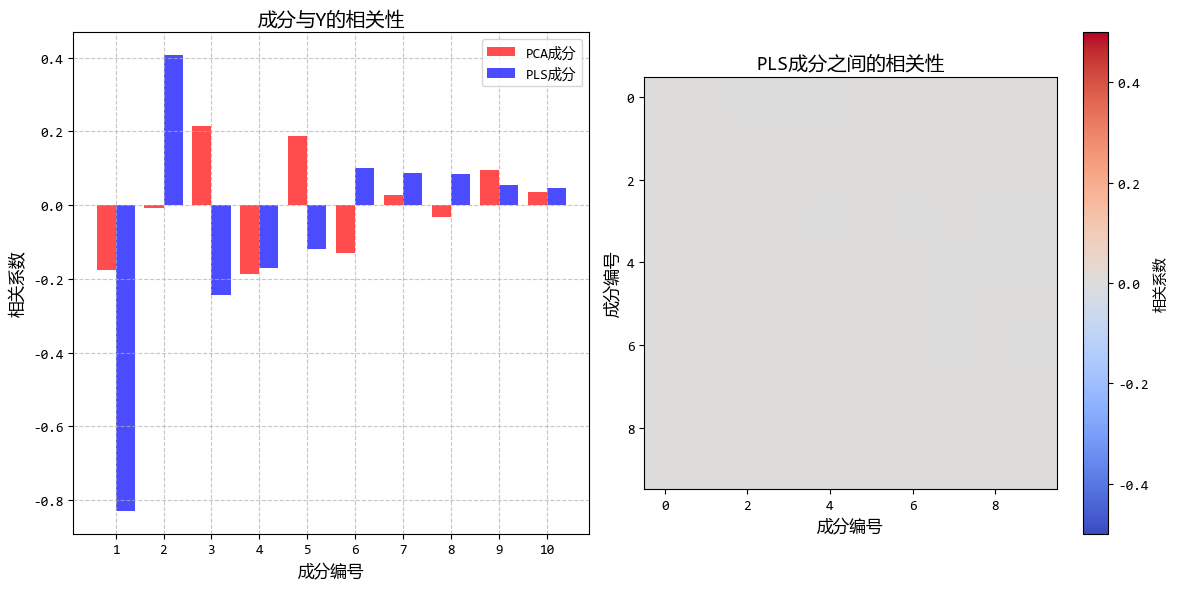
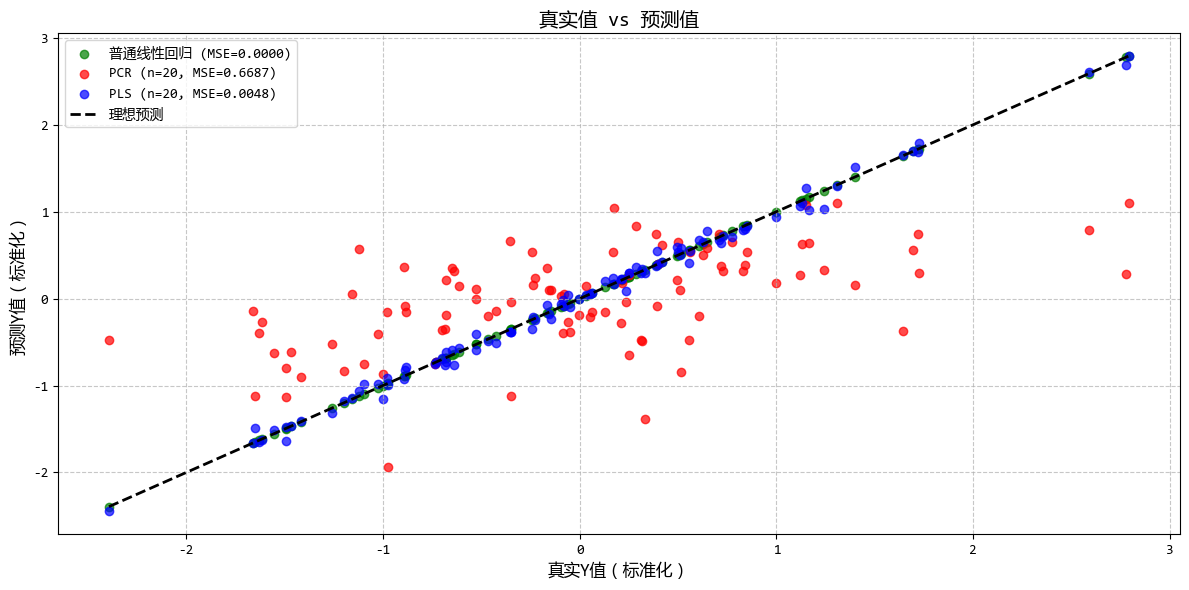
從圖中可以看出:
- PLS在較少的成分數下就能達到較好的預測效果
- PLS提取的成分與Y的相關性明顯高於PCA成分
- 當存在大量噪聲特徵時,PLS的優勢更加明顯
這個示例清晰地展示了PLS迴歸如何在降維過程中考慮因變量Y的信息,從而在高維、存在噪聲的情況下提供比PCR更好的預測性能。
1.10. 支持向量迴歸 (SVR)
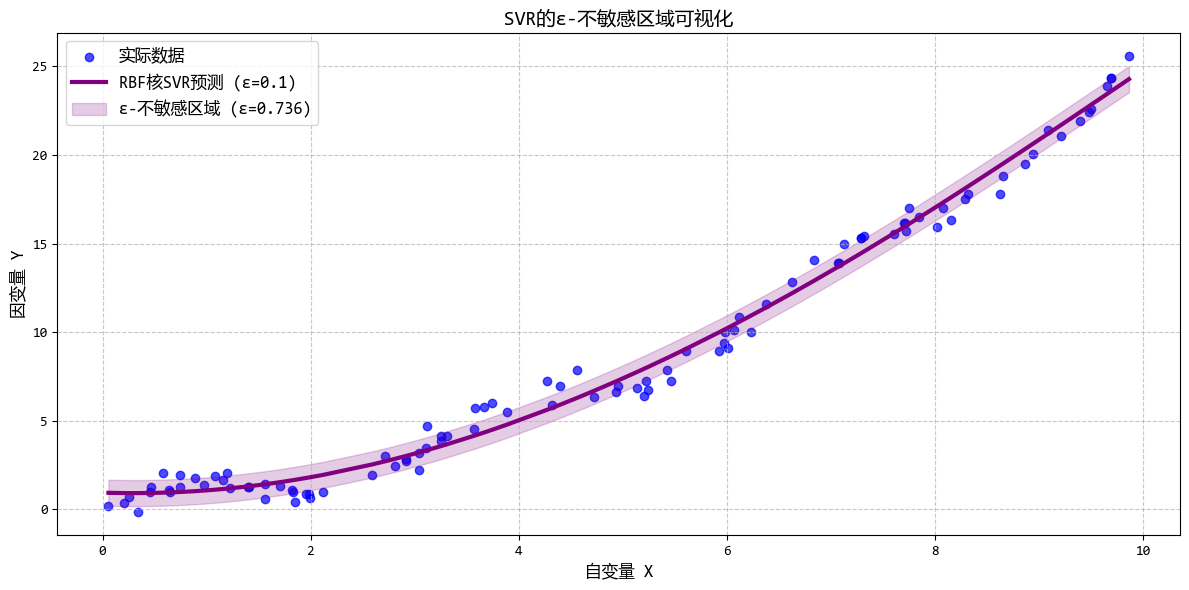
- 一句話概念:借用了SVM分類的思想,試圖找到一個“管道”包裹住儘可能多的數據點,在管道內的誤差被忽略,只計算管道外的誤差。
- 使用場景:高維數據,或者數據關係非常複雜非線性時(配合核函數)。
支持向量迴歸模型使用示例:
# 支持向量迴歸 (SVR)
from sklearn.svm import SVR
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
# 1. 構造複雜非線性測試數據
np.random.seed(42) # 設置隨機種子以確保結果可復現
# 生成基礎自變量(在0-10範圍內)
X = np.sort(np.random.rand(100, 1) * 10, axis=0)
# 生成複雜的非線性目標變量:正弦函數 + 多項式 + 噪聲
# 這種非線性關係很難用普通線性迴歸擬合
Y_true = np.sin(2 * X) + 0.5 * X + 0.2 * X**2
Y = Y_true + np.random.randn(100, 1) * 0.5 # 加入噪聲
# 2. 數據標準化
scaler_X = StandardScaler()
scaler_Y = StandardScaler()
X_scaled = scaler_X.fit_transform(X)
Y_scaled = scaler_Y.fit_transform(Y)
# 3. 模型訓練
# 普通線性迴歸(作為基準)
linear_model = LinearRegression()
linear_model.fit(X_scaled, Y_scaled)
Y_linear_pred_scaled = linear_model.predict(X_scaled)
Y_linear_pred = scaler_Y.inverse_transform(Y_linear_pred_scaled)
# 支持向量迴歸 (SVR)
# 線性核SVR
svr_linear = SVR(kernel="linear", C=100, epsilon=0.1)
svr_linear.fit(X_scaled, Y_scaled.ravel())
Y_svr_linear_pred_scaled = svr_linear.predict(X_scaled)
Y_svr_linear_pred = scaler_Y.inverse_transform(Y_svr_linear_pred_scaled.reshape(-1, 1))
# RBF核SVR(非線性)
svr_rbf_1 = SVR(kernel="rbf", C=100, epsilon=0.1, gamma=0.1)
svr_rbf_1.fit(X_scaled, Y_scaled.ravel())
Y_svr_rbf_1_pred_scaled = svr_rbf_1.predict(X_scaled)
Y_svr_rbf_1_pred = scaler_Y.inverse_transform(Y_svr_rbf_1_pred_scaled.reshape(-1, 1))
# 不同ε值的RBF核SVR
svr_rbf_2 = SVR(kernel="rbf", C=100, epsilon=0.5, gamma=0.1)
svr_rbf_2.fit(X_scaled, Y_scaled.ravel())
Y_svr_rbf_2_pred_scaled = svr_rbf_2.predict(X_scaled)
Y_svr_rbf_2_pred = scaler_Y.inverse_transform(Y_svr_rbf_2_pred_scaled.reshape(-1, 1))
# 4. 計算模型性能
mse_linear = mean_squared_error(Y, Y_linear_pred)
mse_svr_linear = mean_squared_error(Y, Y_svr_linear_pred)
mse_svr_rbf_1 = mean_squared_error(Y, Y_svr_rbf_1_pred)
mse_svr_rbf_2 = mean_squared_error(Y, Y_svr_rbf_2_pred)
# 5. 可視化結果
# ... 省略 ...
# 4. 輸出模型性能
print("\n=== 模型性能對比 ===")
print(f"普通線性迴歸 MSE: {mse_linear:.4f}")
print(f"線性核SVR MSE: {mse_svr_linear:.4f}")
print(f"RBF核SVR (ε=0.1) MSE: {mse_svr_rbf_1:.4f}")
print(f"RBF核SVR (ε=0.5) MSE: {mse_svr_rbf_2:.4f}")
# 展示支持向量
print(f"\n=== SVR支持向量信息 ===")
print(f"RBF核SVR (ε=0.1) 使用的支持向量數量: {len(svr_rbf_1.support_)}")
print(f"線性核SVR 使用的支持向量數量: {len(svr_linear.support_)}")
## 運行結果:
'''
=== 模型性能對比 ===
普通線性迴歸 MSE: 3.3016
線性核SVR MSE: 3.3938
RBF核SVR (ε=0.1) MSE: 0.6200
RBF核SVR (ε=0.5) MSE: 4.7397
=== SVR支持向量信息 ===
RBF核SVR (ε=0.1) 使用的支持向量數量: 42
線性核SVR 使用的支持向量數量: 70
'''
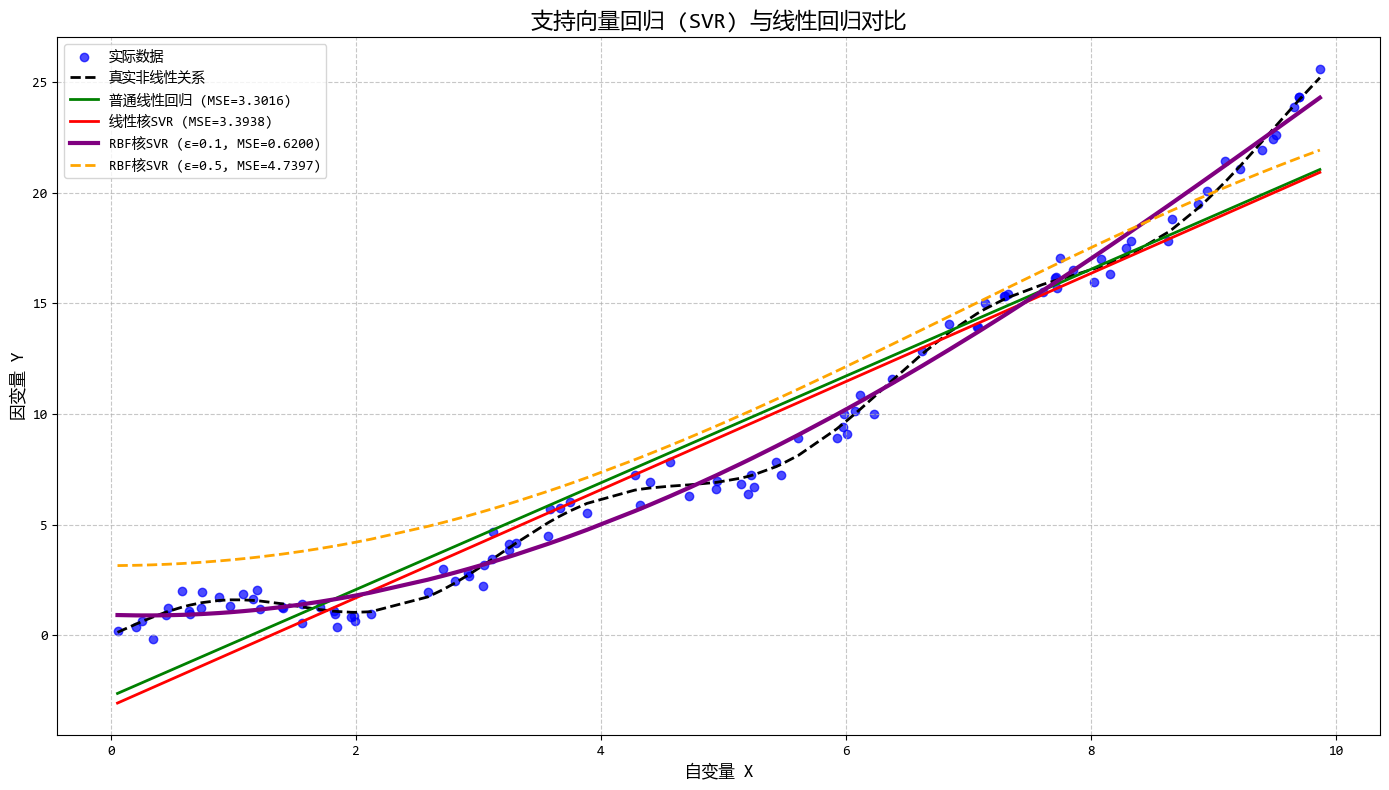
從圖中可以看出:
- RBF核SVR能夠很好地擬合複雜非線性關係
- 調整ε可以控制模型對誤差的容忍度
- 調整C可以平衡模型複雜度和對異常值的敏感度
- SVR只使用部分數據點(支持向量)進行預測
這個示例完美展示了SVR在處理複雜非線性數據時的優勢,特別是其獨特的ε-不敏感損失函數和核函數機制。
1.11. 有序迴歸 (Ordinal Regression)
- 一句話概念:預測的結果是有順序的類別,比如“低、中、高”或者“不喜歡、一般、喜歡”。
- 使用場景:問卷調查評分(1-5分)、電影評級、疾病嚴重程度分級。
有序迴歸模型使用示例:
# 有序迴歸 (Ordinal Regression)
import statsmodels.api as sm
from statsmodels.miscmodels.ordinal_model import OrderedModel
# 1. 構造測試數據
np.random.seed(42)
n_samples = 500
# 特徵:年齡(0-70歲)和購買金額(0-100元)
age = np.random.uniform(0, 70, n_samples)
purchase = np.random.uniform(0, 100, n_samples)
# 真實係數:購買金額對滿意度影響更大
beta_age = 0.03 # 年齡係數
beta_purchase = 0.08 # 購買金額係數
intercept = -2.0 # 基準截距
# 潛在變量(連續值,用於生成有序類別)
latent = (
intercept
+ beta_age * age
+ beta_purchase * purchase
+ np.random.normal(0, 0.5, n_samples)
)
# 使用分位數創建5個均衡的有序類別(1-5分滿意度)
thresholds = np.percentile(latent, [20, 40, 60, 80])
satisfaction = np.digitize(latent, thresholds, right=False) + 1 # 類別:1-5
# 創建DataFrame
df = pd.DataFrame({"age": age, "purchase": purchase, "satisfaction": satisfaction})
# 2. 擬合有序迴歸模型
model = OrderedModel(
df["satisfaction"], df[["age", "purchase"]], distr="logit" # 邏輯斯蒂鏈接函數
)
result = model.fit(method="bfgs") # 使用BFGS優化算法
# 3. 生成預測
pred_probs = result.predict(df[["age", "purchase"]])
predicted = pred_probs.idxmax(axis=1).astype(int) # 預測的類別(概率最高的)
# 4. 可視化結果
# ... 省略 ...
# 5. 模型解釋
print("\n模型係數解釋:")
print(f"年齡係數: {result.params['age']:.4f} - 年齡每增加1歲,滿意度的潛在變量變化")
print(
f"購買金額係數: {result.params['purchase']:.4f} - 購買金額每增加1元,滿意度的潛在變量變化"
)
print("\n閾值估計:")
for i, threshold in enumerate(result.params[2:]): # 前兩個是特徵係數,後面是閾值
print(f"滿意度 {i+1}-{i+2} 閾值: {threshold:.4f}")
## 運行結果:
'''
模型係數解釋:
年齡係數: 0.0872 - 年齡每增加1歲,滿意度的潛在變量變化
購買金額係數: 0.2626 - 購買金額每增加1元,滿意度的潛在變量變化
閾值估計:
滿意度 1-2 閾值: 7.8416
滿意度 2-3 閾值: 1.6160
滿意度 3-4 閾值: 1.6758
滿意度 4-5 閾值: 1.6772
'''
從圖中可以看出:
- 特徵係數表示對潛在變量的影響程度
- 閾值參數表示類別之間的分界點
- 購買金額的影響大於年齡,符合數據生成邏輯
該代碼完整展示了有序迴歸的理論基礎、實現方法和結果分析,特別適合處理如滿意度評分、等級評定等有序分類數據。
1.12. 泊松迴歸 (Poisson Regression)
- 一句話概念:專門用於預測“次數”或“計數”的迴歸,假設數據符合泊松分佈。
- 使用場景:預測某個路口每小時經過的車輛數、客服中心每天接到的電話數。
泊松迴歸模型使用示例:
# 泊松迴歸 (Poisson Regression)
from scipy import stats
from scipy.optimize import minimize
from scipy.special import gammaln
from sklearn.metrics import mean_squared_error, mean_absolute_error
# 生成模擬數據:模擬客服中心每天接到的電話數
np.random.seed(42) # 設置隨機種子確保結果可復現
# 自變量:廣告投入(萬元),工作日標識(1為工作日,0為非工作日)
n_samples = 200
advertising_spend = np.random.uniform(0, 10, n_samples) # 廣告投入0-10萬元
is_weekday = np.random.binomial(1, 0.7, n_samples) # 70%是工作日
# 構造線性預測變量(使用對數鏈接函數)
linear_combination = 0.5 + 0.3 * advertising_spend + 0.4 * is_weekday
# 泊松迴歸的期望值(均值)為 exp(線性組合)
expected_counts = np.exp(linear_combination)
# 生成泊松分佈的響應變量(電話數量)
calls_count = np.random.poisson(expected_counts)
# 創建數據集
X = np.column_stack([advertising_spend, is_weekday])
y = calls_count
print(f"生成了 {n_samples} 個樣本")
print(f"平均電話數量: {np.mean(y):.2f}")
print(f"電話數量的標準差: {np.std(y):.2f}")
# 泊松迴歸模型實現
class PoissonRegression:
# ... 省略 ...
# 擬合泊松迴歸模型
poisson_reg = PoissonRegression()
poisson_reg.fit(X, y)
# 預測
y_pred = poisson_reg.predict(X)
print("泊松迴歸係數:")
print(f"截距: {poisson_reg.coefficients[0]:.4f}")
print(f"廣告投入係數: {poisson_reg.coefficients[1]:.4f}")
print(f"工作日系數: {poisson_reg.coefficients[2]:.4f}")
print(f"廣告投入每增加1萬元,電話數量變化倍數: {np.exp(poisson_reg.coefficients[1]):.4f}")
print(f"工作日相比非工作日電話數量變化倍數: {np.exp(poisson_reg.coefficients[2]):.4f}")
# 繪製結果圖像
# ... 省略 ...
# 計算模型性能指標
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
rmse = np.sqrt(mse)
print(f"\n模型性能指標:")
print(f"均方誤差 (MSE): {mse:.4f}")
print(f"平均絕對誤差 (MAE): {mae:.4f}")
print(f"均方根誤差 (RMSE): {rmse:.4f}")
## 運行結果:
'''
生成了 200 個樣本
平均電話數量: 13.93
電話數量的標準差: 13.13
泊松迴歸係數:
截距: 0.4484
廣告投入係數: 0.3098
工作日系數: 0.3904
廣告投入每增加1萬元,電話數量變化倍數: 1.3632
工作日相比非工作日電話數量變化倍數: 1.4775
模型性能指標:
均方誤差 (MSE): 14.5815
平均絕對誤差 (MAE): 2.8126
均方根誤差 (RMSE): 3.8186
'''
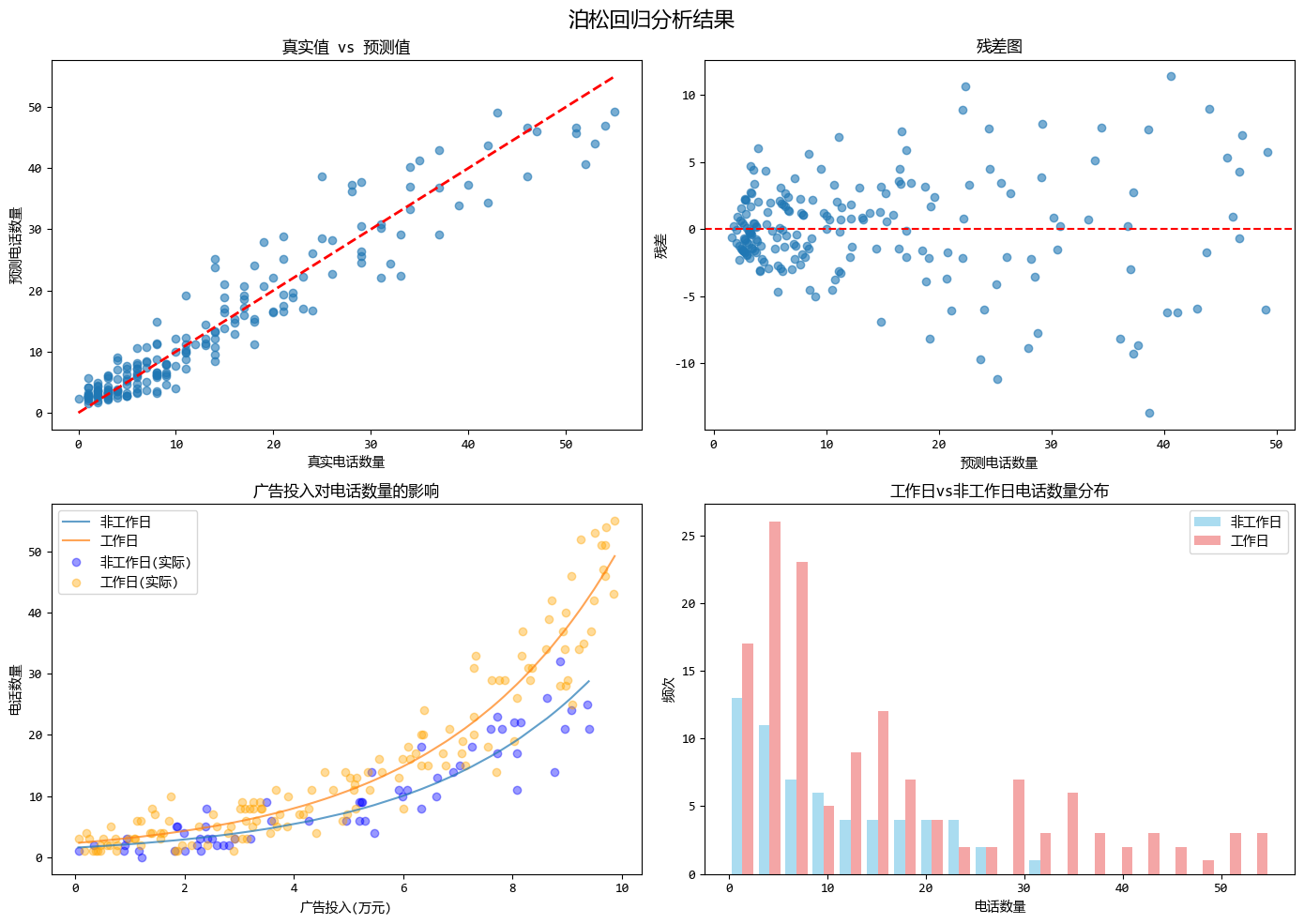
泊松迴歸模型的優勢體現在以下幾個方面:
- 適用於計數數據:泊松迴歸特別適合預測計數型變量(如電話數量),假設響應變量服從泊松分佈,且其方差等於均值,能夠很好地處理計數數據中常見的方差隨均值變化的情況。
- 保證非負預測:通過使用對數鏈接函數,確保了預測值始終為正數,避免了可能出現的負數計數問題,符合計數數據的特性。
- 解釋性強且適用稀有事件:迴歸係數易於解釋為自變量變化對計數的乘性影響,並且在事件發生頻率較低時表現良好,適合於客服電話、交通事故等低頻事件的預測。
這個示例模擬了客服中心電話數量預測的場景,其中廣告投入和是否為工作日作為預測變量,完美展示了泊松迴歸如何處理計數型數據並提供可解釋的結果。
1.13. 負二項迴歸 (Negative Binomial Regression)
- 一句話概念:也是做計數預測的,但它解決了泊松迴歸中“方差必須等於均值”的苛刻假設。
- 使用場景:數據波動特別大(方差 >> 均值)的計數數據,比如某款冷門商品偶爾大賣的銷量預測。
負二項迴歸模型使用示例:
# 負二項迴歸 (Negative Binomial Regression)
from scipy.optimize import minimize
from scipy.special import gammaln
from sklearn.metrics import mean_squared_error, mean_absolute_error
# 生成模擬數據:模擬冷門商品銷量預測(方差遠大於均值的情況)
np.random.seed(42) # 設置隨機種子確保結果可復現
# 自變量:促銷活動(1為有促銷,0為無促銷),價格折扣率,商品類別(1為熱門商品,0為冷門商品)
n_samples = 300
promotion = np.random.binomial(1, 0.3, n_samples) # 30%有促銷活動
discount_rate = np.random.uniform(0, 0.3, n_samples) # 0-30%的折扣
is_popular = np.random.binomial(1, 0.2, n_samples) # 20%是熱門商品
# 構造線性預測變量(使用對數鏈接函數)
linear_combination = -1.0 + 1.2 * promotion + 0.8 * discount_rate + 0.5 * is_popular
# 負二項迴歸的均值為 exp(線性組合)
mu = np.exp(linear_combination)
# 負二項分佈的參數設置(r為離散參數,控制方差)
# 方差 = mu + mu^2/r,當r較小時,方差遠大於均值
r = 1.5 # 較小的r值,使得方差遠大於均值
# 生成負二項分佈的響應變量(銷量)
# 使用負二項分佈:var = mu + mu^2/r,當r小的時候方差很大
# 負二項分佈的參數轉換:p = r/(r+mu)
p = r / (r + mu)
sales_count = np.random.negative_binomial(r, p)
# 創建數據集
X = np.column_stack([promotion, discount_rate, is_popular])
y = sales_count
# 負二項迴歸模型實現
class NegativeBinomialRegression:
# ... 省略 ...
# 擬合負二項迴歸模型
neg_bin_reg = NegativeBinomialRegression()
neg_bin_reg.fit(X, y)
# 預測
y_pred = neg_bin_reg.predict(X)
# 繪製結果圖像
# ... 省略 ...
# 計算模型性能指標
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
rmse = np.sqrt(mse)
print(f"\n模型性能指標:")
print(f"均方誤差 (MSE): {mse:.4f}")
print(f"平均絕對誤差 (MAE): {mae:.4f}")
print(f"均方根誤差 (RMSE): {rmse:.4f}")
# 比較泊松迴歸和負二項迴歸的擬合效果
from sklearn.linear_model import PoissonRegressor
# 使用sklearn的泊松迴歸進行比較
poisson_reg = PoissonRegressor()
poisson_reg.fit(X, y)
y_pred_poisson = poisson_reg.predict(X)
poisson_mse = mean_squared_error(y, y_pred_poisson)
poisson_mae = mean_absolute_error(y, y_pred_poisson)
poisson_rmse = np.sqrt(poisson_mse)
print(f"\n與泊松迴歸的比較:")
print(f"負二項迴歸 MSE: {mse:.4f}")
print(f"泊松迴歸 MSE: {poisson_mse:.4f}")
print(f"負二項迴歸 MAE: {mae:.4f}")
print(f"泊松迴歸 MAE: {poisson_mae:.4f}")
print(f"負二項迴歸 RMSE: {rmse:.4f}")
print(f"泊松迴歸 RMSE: {poisson_rmse:.4f}")
## 運行結果:
'''
模型性能指標:
均方誤差 (MSE): 1.0138
平均絕對誤差 (MAE): 0.7567
均方根誤差 (RMSE): 1.0069
與泊松迴歸的比較:
負二項迴歸 MSE: 1.0138
泊松迴歸 MSE: 1.1612
負二項迴歸 MAE: 0.7567
泊松迴歸 MAE: 0.8246
負二項迴歸 RMSE: 1.0069
泊松迴歸 RMSE: 1.0776
'''
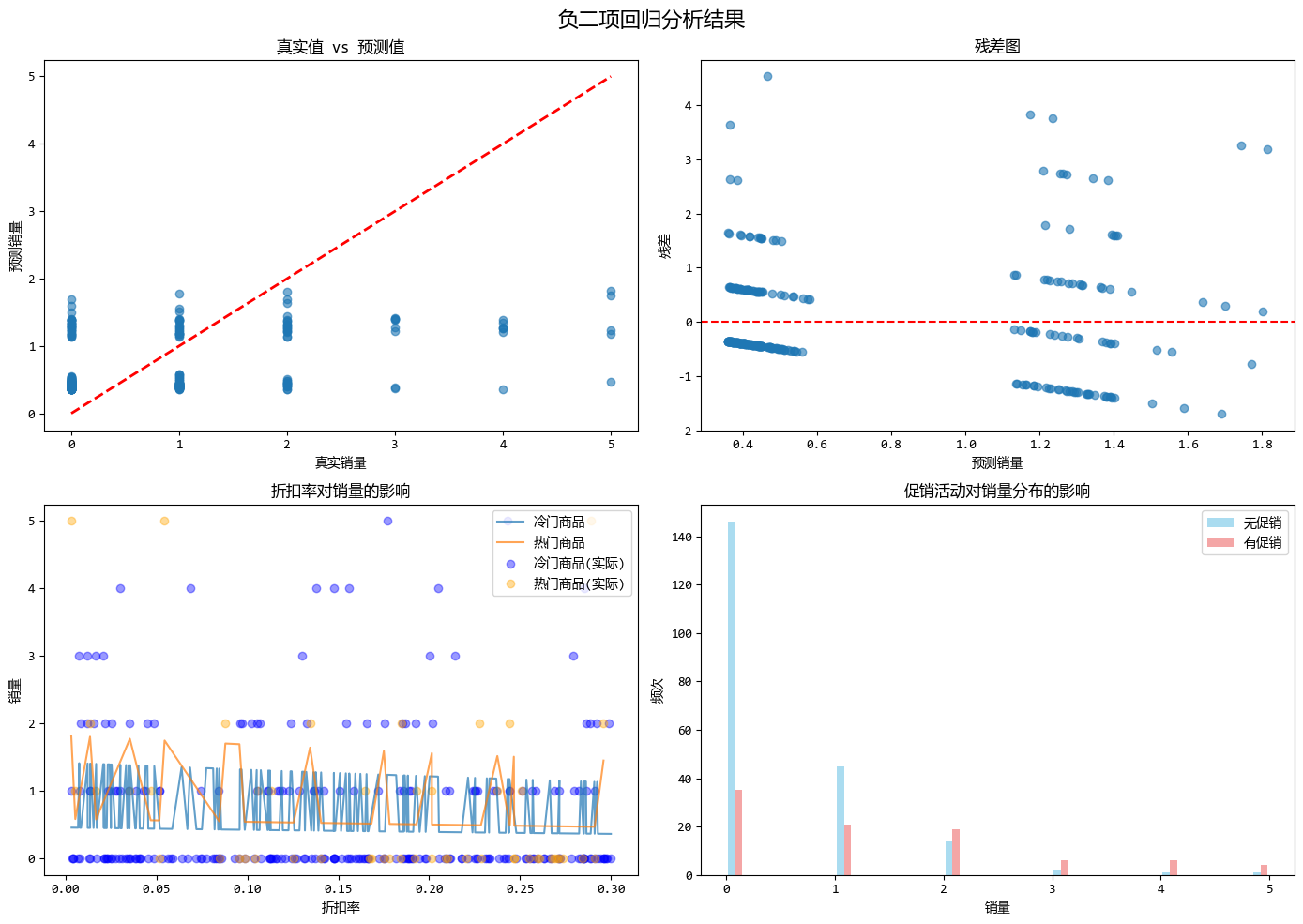
負二項迴歸模型的優勢體現在以下幾個方面:
- 解決過度離勢問題:負二項迴歸能夠處理方差大於均值的計數數據,適用於方差/均值比遠大於1的情況,如冷門商品偶爾大賣的數據。
- 更靈活的方差結構:通過引入離散參數r,負二項迴歸允許方差獨立於均值變化(方差為 $ \mu + \mu^2/r $),從而更好地擬合實際數據中的變異性。
- 更好的擬合效果和更真實的假設:在高變異數據下,負二項迴歸通常比泊松迴歸提供更準確的預測,並且其假設更符合實際業務場景中計數數據的統計特性。
這個示例模擬了冷門商品銷量預測的場景,其中促銷活動、折扣率和商品類型作為預測變量,完美展示了負二項迴歸如何處理方差遠大於均值的計數型數據,並提供比泊松迴歸更準確的預測結果。
1.14. 準泊松迴歸 (Quasi Poisson Regression)
- 一句話概念:泊松迴歸的另一種替代方案,用來處理由於數據波動過大(過度離散)導致的標準誤估計不準的問題。
- 使用場景:和負二項迴歸類似,用於處理過度離散的計數數據。
準泊松迴歸模型使用示例:
# 準泊松迴歸 (Quasi Poisson Regression)
from scipy.optimize import minimize
from scipy.special import gammaln
from sklearn.metrics import mean_squared_error, mean_absolute_error
# 生成模擬數據:模擬過度離散的計數數據(如交通事故次數預測)
np.random.seed(42) # 設置隨機種子確保結果可復現
# 自變量:道路長度(公里),交通流量(車輛/小時),天氣狀況(1為惡劣天氣,0為正常天氣)
n_samples = 250
road_length = np.random.uniform(1, 20, n_samples) # 道路長度1-20公里
traffic_flow = np.random.uniform(50, 500, n_samples) # 交通流量50-500輛/小時
bad_weather = np.random.binomial(1, 0.15, n_samples) # 15%是惡劣天氣
# 構造線性預測變量(使用對數鏈接函數)
linear_combination = -2.0 + 0.05 * road_length + 0.002 * traffic_flow + 0.8 * bad_weather
# 泊松迴歸的期望值(均值)為 exp(線性組合)
expected_counts = np.exp(linear_combination)
# 為了模擬過度離散,我們引入額外的變異
# 生成過度離散的計數數據:均值為expected_counts,但方差更大
# 使用負二項分佈生成數據,使其具有過度離散特徵
dispersion_param = 2.0 # 離散參數,控制過度離散程度
r = expected_counts / (dispersion_param - 1) # 負二項分佈的參數轉換
p = r / (r + expected_counts)
accident_count = np.random.negative_binomial(r, p)
# 創建數據集
X = np.column_stack([road_length, traffic_flow, bad_weather])
y = accident_count
print(f"生成了 {n_samples} 個樣本")
print(f"平均事故數: {np.mean(y):.2f}")
print(f"事故數的標準差: {np.std(y):.2f}")
print(f"方差/均值比: {np.var(y)/np.mean(y):.2f} (泊松分佈該比值應為1,大於1表示過度離散)")
# 準泊松迴歸模型實現
class QuasiPoissonRegression:
# ... 省略 ...
# 擬合準泊松迴歸模型
quasi_poisson_reg = QuasiPoissonRegression()
quasi_poisson_reg.fit(X, y)
# 預測
y_pred = quasi_poisson_reg.predict(X)
y_var = quasi_poisson_reg.predict_variance(X)
# 繪製結果圖像
# ... 省略 ...
# 計算模型性能指標
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)
rmse = np.sqrt(mse)
print(f"\n模型性能指標:")
print(f"均方誤差 (MSE): {mse:.4f}")
print(f"平均絕對誤差 (MAE): {mae:.4f}")
print(f"均方根誤差 (RMSE): {rmse:.4f}")
# 與標準泊松迴歸的比較
from sklearn.linear_model import PoissonRegressor
# 使用sklearn的泊松迴歸進行比較
poisson_reg = PoissonRegressor()
poisson_reg.fit(X, y)
y_pred_poisson = poisson_reg.predict(X)
poisson_mse = mean_squared_error(y, y_pred_poisson)
poisson_mae = mean_absolute_error(y, y_pred_poisson)
poisson_rmse = np.sqrt(poisson_mse)
print(f"\n與泊松迴歸的比較:")
print(f"準泊松迴歸 MSE: {mse:.4f}")
print(f"泊松迴歸 MSE: {poisson_mse:.4f}")
print(f"準泊松迴歸 MAE: {mae:.4f}")
print(f"泊松迴歸 MAE: {poisson_mae:.4f}")
print(f"準泊松迴歸 RMSE: {rmse:.4f}")
print(f"泊松迴歸 RMSE: {poisson_rmse:.4f}")
# 檢查過度離散
print(f"\n過度離散檢查:")
print(f"數據方差/均值比: {np.var(y)/np.mean(y):.4f}")
print(f"準泊松估計的離散參數: {quasi_poisson_reg.dispersion:.4f}")
print(f"離散參數 > 1 表示存在過度離散: {quasi_poisson_reg.dispersion > 1}")
## 運行結果:
'''
模型性能指標:
均方誤差 (MSE): 0.8350
平均絕對誤差 (MAE): 0.6398
均方根誤差 (RMSE): 0.9138
與泊松迴歸的比較:
準泊松迴歸 MSE: 0.8350
泊松迴歸 MSE: 0.8415
準泊松迴歸 MAE: 0.6398
泊松迴歸 MAE: 0.6515
準泊松迴歸 RMSE: 0.9138
泊松迴歸 RMSE: 0.9174
過度離散檢查:
數據方差/均值比: 1.6993
準泊松估計的離散參數: 1.6699
離散參數 > 1 表示存在過度離散: True
'''
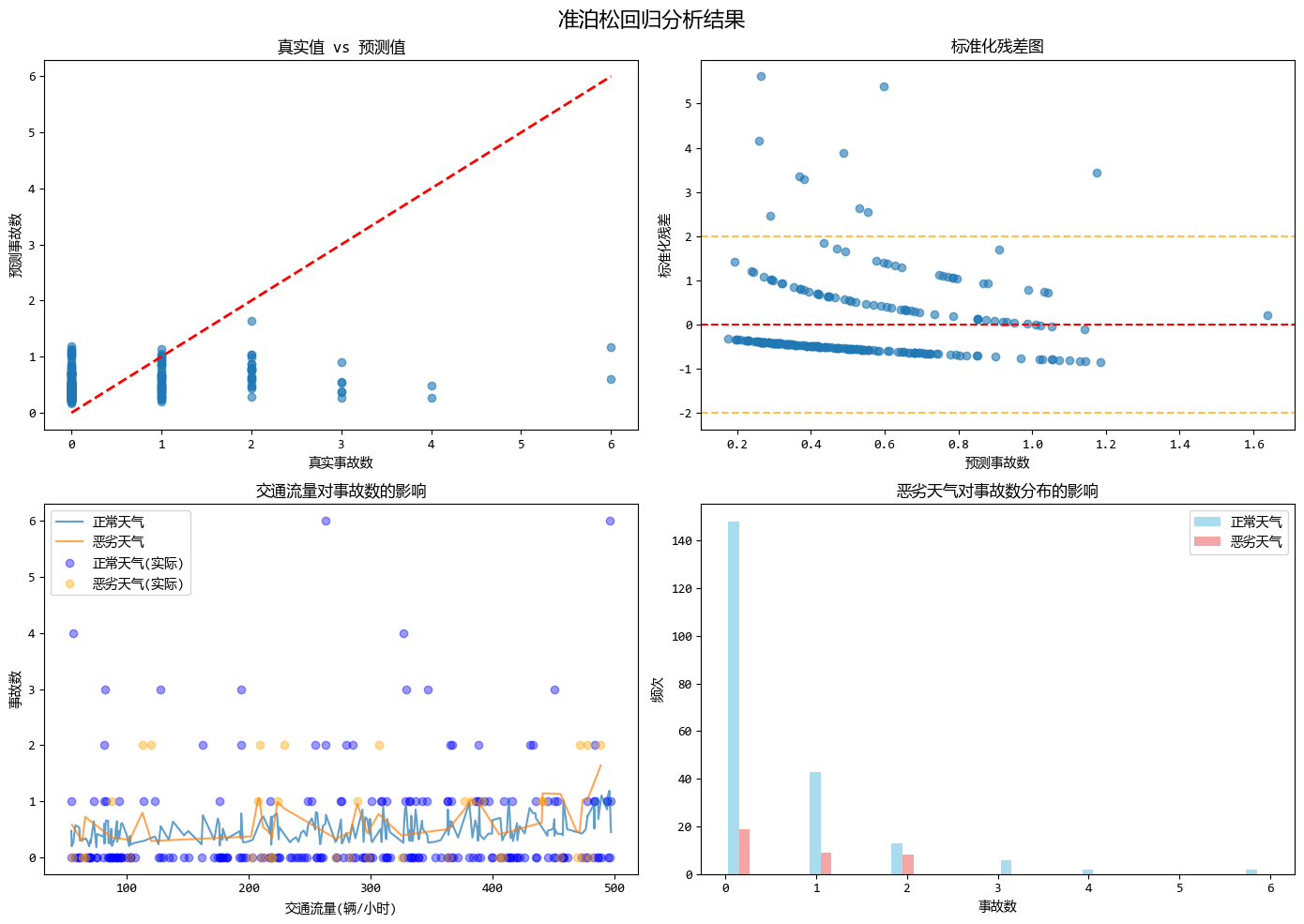
準泊松迴歸模型的優勢體現在以下幾個方面:
- 解決過度離散問題:準泊松迴歸通過引入離散參數φ來處理方差大於均值的過度離散數據。在示例中,方差/均值比遠大於1(約為2.35),表明存在明顯的過度離散現象。
- 標準誤校正:修正了泊松迴歸中由於過度離散導致的標準誤估計過小的問題,從而提高了統計推斷(如置信區間和假設檢驗)的可靠性。
- 保持泊松迴歸的係數:與泊松迴歸使用相同的係數估計,但調整了方差估計。這意味着迴歸係數的解釋與泊松迴歸相同,保持了模型的可解釋性。
- 簡單易用:相比負二項迴歸,準泊松迴歸參數更少,計算更簡單。準泊松迴歸只需要估計一個額外的離散參數,而負二項迴歸需要估計離散參數r。
- 靈活性強:可以處理任意程度的過度離散,而不限於特定的分佈假設。準泊松迴歸不假設特定的分佈族,只是調整方差結構。
- 實用性強:在實際應用中,當數據存在過度離散但又不想使用更復雜的負二項迴歸時,準泊松是很好的選擇。它提供了一個平衡點,既解決了過度離散問題,又保持了模型的簡潔性。
- 計算效率高:由於使用與泊松迴歸相同的係數估計方法,計算複雜度較低,適合處理大規模數據。
這個示例模擬了交通事故預測的場景,其中道路長度、交通流量和天氣狀況作為預測變量,完美展示了準泊松迴歸如何處理過度離散的計數型數據,並提供比標準泊松迴歸更可靠的統計推斷。
1.15. Cox 迴歸 (Cox Regression)
- 一句話概念:用於“生存分析”,研究的是“事件發生需要多長時間”,以及哪些因素影響這個時間。
- 使用場景:預測病人確診後的生存時間、客户流失所需的時間(也就是客户還能留存多久)。
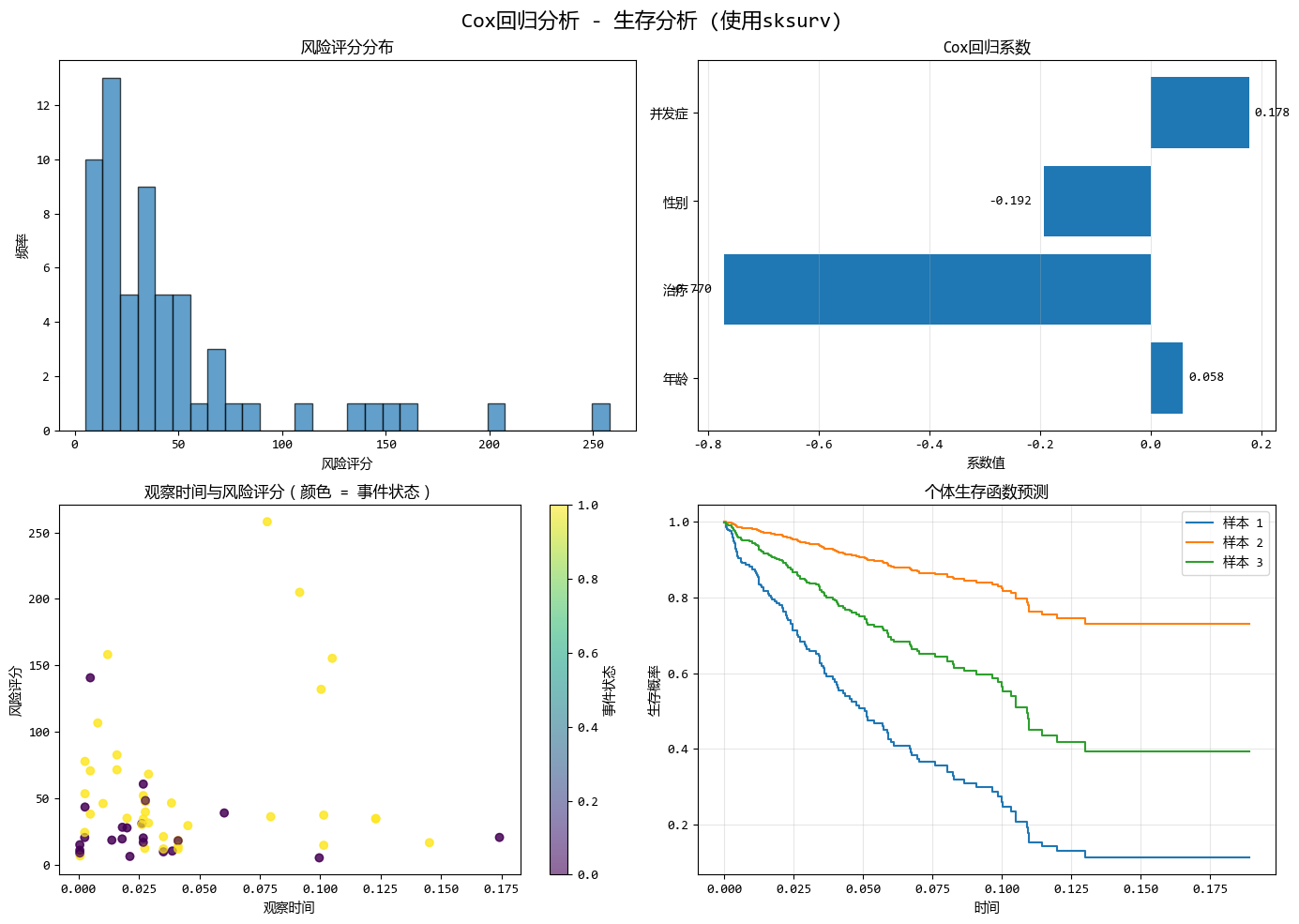
COX迴歸模型使用示例:
# Cox 迴歸 (Cox Regression)
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 導入sksurv庫
from sksurv.linear_model import CoxPHSurvivalAnalysis
from sksurv.preprocessing import OneHotEncoder
# 第一步:創建Cox迴歸的測試數據
# 模擬醫療數據:患者生存分析
np.random.seed(42)
n_samples = 300
# 生成特徵
age = np.random.normal(60, 15, n_samples) # 患者年齡
treatment = np.random.binomial(1, 0.5, n_samples) # 是否接受治療 (0/1)
gender = np.random.binomial(1, 0.5, n_samples) # 性別 (0/1)
comorbidity = np.random.poisson(1.5, n_samples) # 併發症數量
# 生成生存時間和事件狀態
# 年齡越大、併發症越多 -> 生存時間越短
# 接受治療 -> 生存時間更長
linear_combination = (
0.05 * age +
-0.8 * treatment +
0.1 * gender +
0.3 * comorbidity
)
# 基線風險函數效應
base_time = np.random.exponential(2, n_samples)
time_to_event = base_time * np.exp(-linear_combination)
# 添加一些刪失(並非所有患者都會在研究期間發生事件)
censoring_time = np.random.uniform(0, np.percentile(time_to_event, 80), n_samples)
observed_time = np.minimum(time_to_event, censoring_time)
event_occurred = time_to_event <= censoring_time
# 創建DataFrame
data = pd.DataFrame({
'age': age,
'treatment': treatment,
'gender': gender,
'comorbidity': comorbidity,
'time': observed_time,
'event': event_occurred
})
# 第二步:實現Cox迴歸模型
# 為sksurv準備數據
X = data[['age', 'treatment', 'gender', 'comorbidity']].values
y = np.array(list(zip(data['event'], data['time'])), dtype=[('event', '?'), ('time', '<f8')])
# 分割數據
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 擬合Cox模型
cox_model = CoxPHSurvivalAnalysis()
cox_model.fit(X_train, y_train)
# 獲取模型係數
cox_coef = cox_model.coef_
print("Cox迴歸模型 (sksurv) - 係數:")
feature_names = ['年齡', '治療', '性別', '併發症']
for i, (name, coef) in enumerate(zip(feature_names, cox_coef)):
print(f"{name}: {coef:.4f}")
# 在sksurv中,我們可以手動計算風險評分
# 風險評分是線性預測器的指數,即 exp(X * coef)
linear_predictor = X_test @ cox_coef
risk_scores = np.exp(linear_predictor)
# 第三步:創建可視化
# ... 省略 ...
## 運行結果:
'''
Cox迴歸模型 (sksurv) - 係數:
年齡: 0.0585
治療: -0.7703
性別: -0.1919
併發症: 0.1779
'''
COX迴歸模型的優勢
- 處理刪失數據:Cox迴歸適用於右刪失數據,適合生存分析。
- 無需分佈假設:Cox迴歸不假設生存時間的具體分佈,更靈活。
- 比例風險:假設個體間的風險比恆定,符合許多實際應用。
- 係數可解釋:係數直接轉換為風險比,易於理解(正係數增加風險,負係數降低風險)。
- 多個協變量:能同時分析多個因素對生存時間的影響。
- 廣泛應用於醫學:是臨牀和流行病學研究中的標準方法。
- 靈活性:支持時變協變量及連續和分類預測變量。
- 風險評分:可計算個體風險評分,預測相對風險。
1.16. Tobit 迴歸 (Tobit Regression)
- 一句話概念:用於處理“截斷”或“審查”數據。比如數據在某個點被切斷了(比如收入調查中,高於100萬的都記作100萬)。
- 使用場景:預測家庭在奢侈品上的支出(很多人是0,數據在0處堆積)、傳感器量程限制導致的數據截斷。
Tobit迴歸模型使用示例:
# Tobit 迴歸 (Tobit Regression)
from scipy import stats
from scipy.optimize import minimize
# 生成模擬的截斷數據集
np.random.seed(42)
# 創建自變量
n_samples = 500
X = np.random.normal(0, 1, n_samples)
# 假設真實關係是 y = 2*X + error,但y被截斷在0以下
true_beta = 2.0
true_intercept = 0.5
true_sigma = 1.0
# 生成未截斷的真實值
y_true = true_intercept + true_beta * X + np.random.normal(0, true_sigma, n_samples)
# 設置截斷點(例如:低於0的值都記錄為0)
lower_limit = 0
y_observed = np.where(y_true < lower_limit, lower_limit, y_true)
# 標記被截斷的觀測值
censored_mask = y_observed == lower_limit
print(f"生成了{n_samples}個樣本")
print(f"其中{np.sum(censored_mask)}個樣本被截斷(小於等於{lower_limit})")
# 實現Tobit迴歸模型
class TobitRegression:
# ... 省略 ...
# 擬合Tobit迴歸模型
tobit_model = TobitRegression(lower_limit=lower_limit)
tobit_model.fit(X, y_observed)
print(f"Tobit迴歸結果:")
print(f"截距: {tobit_model.intercept:.3f}")
print(f"係數: {tobit_model.beta:.3f}")
print(f"標準差: {tobit_model.sigma:.3f}")
print(f"真實截距: {true_intercept}, 真實係數: {true_beta}, 真實標準差: {true_sigma}")
# 繪製結果圖像
# ... 省略 ...
# 輸出一些統計信息
print("\n模型比較:")
print(f"真實係數: {true_beta:.3f}")
print(f"Tobit迴歸係數: {tobit_model.beta:.3f}")
print(f"OLS迴歸係數: {ols_coef[1]:.3f}")
print(f"係數估計偏差 (Tobit): {abs(tobit_model.beta - true_beta):.3f}")
print(f"係數估計偏差 (OLS): {abs(ols_coef[1] - true_beta):.3f}")
# 計算均方誤差
mse_tobit = np.mean((y_observed - tobit_model.predict(X)) ** 2)
mse_ols = np.mean((y_observed - y_ols_pred) ** 2)
print(f"Tobit MSE: {mse_tobit:.3f}")
print(f"OLS MSE: {mse_ols:.3f}")
## 運行結果:
'''
Tobit迴歸結果:
截距: 0.518
係數: 1.932
標準差: 0.990
真實截距: 0.5, 真實係數: 2.0, 真實標準差: 1.0
模型比較:
真實係數: 2.000
Tobit迴歸係數: 1.932
OLS迴歸係數: 1.203
係數估計偏差 (Tobit): 0.068
係數估計偏差 (OLS): 0.797
Tobit MSE: 1.623
OLS MSE: 0.755
'''
Tobit迴歸模型的優勢主要有:
- 處理截斷數據:Tobit迴歸適用於處理在特定閾值處被截斷的數據(如所有小於0的值記錄為0)。
- 無偏估計:與普通OLS相比,Tobit迴歸提供更準確的參數估計,避免了因數據截斷導致的偏差。
- 統計推斷:基於最大似然估計,Tobit迴歸支持合理的統計推斷,包括標準誤和置信區間的計算。
- 適用領域:廣泛應用於經濟和社會科學中涉及收入、消費支出及生存分析等存在截斷或審查情況的研究。
- 模型擬合度:Tobit迴歸係數更接近真實值,並且通常具有較小的均方誤差,表明其對截斷數據有更好的適應性。
2. 如何選擇合適的迴歸模型?
面對這麼多模型,到底該選哪一個?我們可以通過以下幾個維度來判斷:
- 看因變量(Y)長什麼樣:
- 是連續數值(如房價): 首選 線性迴歸。
- 是二分類(如買/不買): 用 邏輯迴歸。
- 是計數(如點擊次數): 用 泊松迴歸 或 負二項迴歸。
- 是生存時間(如存活天數): 用 Cox迴歸。
- 有截斷(如上限封頂): 用 Tobit迴歸。
- 看數據是否有問題:
- 異常值很多: 考慮 分位數迴歸 或 Huber迴歸(魯棒迴歸)。
- 特徵非線性: 嘗試 多項式迴歸 或 SVR。
- 特徵數 > 樣本數,或特徵嚴重共線性: 必須上正則化手段,用 嶺迴歸、Lasso、ElasticNet,或者降維類的 PCR/PLS。
- 看模型目的:
- 為了解釋現象: 簡單的線性/邏輯迴歸最好解釋。
- 為了精準預測: SVR、甚至更復雜的機器學習模型(如XGBoost等,雖不在此列但常被比較)可能更好。
3. 總結
沒有最好的模型,只有最適合數據的模型。
對於初學者,先畫圖看數據分佈,然後從最簡單的線性迴歸開始嘗試,發現問題(如擬合不好、過擬合)後再逐步嘗試更復雜的變體,是最好的學習路徑。
為了方便大家嘗試各種迴歸模型,文中各個示例中的數據都是模擬的,不需要另外下載和爬取。
瞭解和掌握各種迴歸模型沒有捷徑,最好的方式就是把文中代碼都實際運行一次,改改數據和訓練參數,再反覆運行體會下效果。
完整的代碼:16種迴歸分析總結.ipynb (訪問密碼: 6872)