在數據分析的江湖裏,有一個絕對的核心技能,叫做迴歸分析(Regression Analysis)。
無論你是剛入行的新手,還是想要進階的老手,掌握它,你就擁有了預測未來的“水晶球”。
很多初學者一聽到“迴歸”兩個字,腦子裏全是複雜的數學公式,立刻想打退堂鼓。
別急!今天我們不講枯燥的數學推導,只講它是什麼、怎麼用,以及如何用Python代碼解決實際問題。
1. 什麼是迴歸分析?
想象一下,你正在做飯。你知道火開得越大(變量X),鍋裏的水燒開的時間就越短(變量Y)。這種探尋變量之間因果關係或相關關係的過程,就是迴歸分析。
在數據分析中,迴歸分析主要幫我們解決兩個問題:
- 歸因:是誰影響了結果?(比如:是學歷還是工作經驗決定了你的薪資?)
- 預測:根據現有數據推測未來。(比如:根據上個月的廣告費,預測下個月的銷量。)
2. 線性迴歸:一切的起點
線性迴歸是最簡單、最基礎的模型,它假設變量之間的關係是一條直線。
2.1. 簡單線性迴歸
公式:$ y = ax + b $
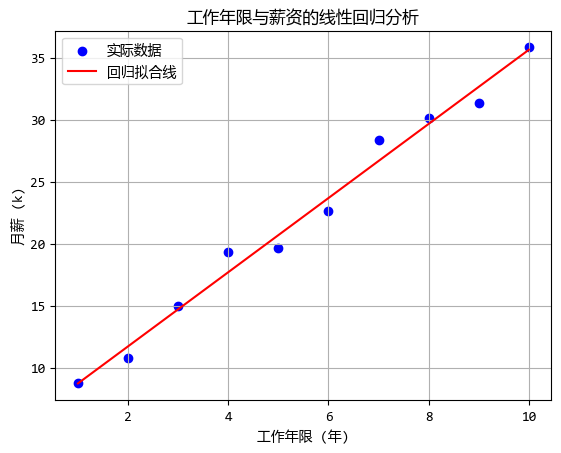
比如我們要研究 “工作經驗”和“薪資”的關係。
- $ x $:工作年限
- $ y $:月薪
這裏的核心是找到那個最好的 $ a $(斜率,代表經驗每增加一年,工資漲多少)和 $ b $(截距,代表剛畢業時的起薪)。
我們通常使用最小二乘法,簡單來説,就是畫一條線,讓所有實際的數據點到這條線的距離之和最小。
代碼示例:預測你的薪資
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 1. 模擬數據:工作年限 vs 月薪 (單位:千元)
# 真實世界中數據總會有波動(加上一些隨機噪聲)
np.random.seed(42)
X = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1) # 工作年限
y = 3 * X + 5 + np.random.normal(0, 1.5, size=(10, 1)) # 假設大概規律是:起薪5k,每年漲3k
# 2. 建立模型並訓練
model = LinearRegression()
model.fit(X, y)
# 3. 打印迴歸係數
print(f"迴歸方程: y = {model.coef_[0][0]:.2f} * x + {model.intercept_[0]:.2f}")
print("解讀:起薪約 {:.2f}k,每年約漲 {:.2f}k".format(model.intercept_[0], model.coef_[0][0]))
# 運行結果:
'''
迴歸方程: y = 2.99 * x + 5.73
解讀:起薪約 5.73k,每年約漲 2.99k
'''
2.2. 多元線性迴歸
現實生活中,影響薪資的不止是年限,還有學歷、所在城市等。
當自變量 $ x $ 變成多個($ x_1, x_2, ... $)時,這就是多元線性迴歸。
雖然超過3維畫圖比較困難,但Python處理起來代碼幾乎和簡單線性迴歸一樣,只是把 $ X $ 數據集多加幾列而已。
3. 非線性迴歸:現實世界通常是彎曲的
並不是所有關係都是直線的。比如:
- 細菌分裂:一開始很少,突然爆發(指數函數)。
- 學習曲線:剛開始進步快,後面越來越慢(對數函數)。
- 網紅產品生命週期:爆發增長 -> 趨於飽和(S曲線/邏輯函數)。
針對這些非線性關係,我們需要用到不同的“數學模型”來擬合。
以下是 **10種常用非線性模型 **的公式。
我們將使用 Python 的 scipy.optimize.curve_fit 庫,這個庫非常強大,只要你給出公式,它就能幫你找到參數。
import numpy as np
# --- 定義各種非線性函數 ---
# 1. 二次式 (拋物線,如投籃軌跡)
def func_quadratic(x, a, b, c):
return a * x**2 + b * x + c
# 2. 三次式 (波動更復雜的數據)
def func_cubic(x, a, b, c, d):
return a * x**3 + b * x**2 + c * x + d
# 3. 增長函數 (常用於人口增長、複利計算)
def func_growth(x, a, b):
return np.exp(a * x + b)
# 4. 冪函數 (如物理學中的萬有引力、規模效應)
def func_power(x, a, b):
return a * (x ** b)
# 5. 指數函數 (病毒傳播初期)
def func_exponential(x, a, b):
return a * np.exp(b * x)
# 6. 對數函數 (邊際效應遞減,如廣告投入與銷量的後期關係)
def func_logarithmic(x, a, b):
# 防止x為0報錯,通常處理為 x+1 或確保數據 > 0
return a * np.log(x) + b
# 7. 複合函數 (根據具體複合形式定義,此處示例 y = a * b^x)
def func_compound(x, a, b):
return a * (b ** x)
# 8. S曲線 (S-Curve, 早期慢,中期快,晚期平緩)
def func_scurve(x, a, b):
return np.exp(a + b / x)
# 9. 逆函數 (雙曲線,如某種反比關係)
def func_inverse(x, a, b):
return a + b / x
# 10. 邏輯函數 (Logistic, 典型的S型增長,有上限,如市場滲透率)
# u: 上限, a, b: 形狀參數
def func_logistic(x, u, a, b):
return 1 / (1/u + a * (b ** x))
| 模型類型 | 數學形式 | 實際案例 | 關鍵特徵 |
|---|---|---|---|
| 二次式模型 | $ y=ax^2+bx+c $ | 1. 廣告投入與銷售額(邊際遞減)
2. 生產成本與產量(U型成本曲線) 3. 車速與燃油效率 |
• 只有一個極值點
• 描述先增後減或先減後增 • 適合局部非線性 |
| 三次式模型 | $ y=ax3+bx2+cx+d $ | 1. 經濟週期波動分析
2. 複雜化學反應速率 3. 生物生長多階段模型 |
• 可有多個極值點
• 描述S型或N型曲線 • 靈活但易過擬合 |
| 增長函數 | $ y=e^{(ax+b)} $ | 1. 病毒傳播初期
2. 初創公司用户增長 3. 複利計算 |
• J型增長曲線
• 增長率恆定 • 無上限增長 |
| 冪函數 | $ y=ax^b $ | 1. 代謝率與體重(克萊伯定律)
2. 城市規模與經濟產出 3. 學習曲線(熟練度提升) |
• 雙對數座標下呈直線
• 描述規模效應 • b>1:超線性;b<1:次線性 |
| 指數函數 | $ y=ae^{bx} $ | 1. 放射性物質衰變
2. 設備折舊計算 3. 温度冷卻過程 |
• 半對數座標下呈直線
• b>0:指數增長 • b<0:指數衰減 |
| 對數函數 | $ y=a\ln x+b $ | 1. 技能提升曲線
2. 營銷效果遞減 3. 收入與幸福感關係 |
• 初期增長迅速
• 後期趨於平緩 • 描述邊際遞減效應 |
| 複合函數 | $ y=a^xb $ | 1. 技術創新擴散
2. 社交媒體信息傳播 3. 某些生物種羣增長 |
• 變量在指數位置
• 增長速率不斷變化 • 形式較為特殊 |
| S曲線 | $ y=e^{(a+\frac{b}{x})} $ | 1. 產品生命週期
2. 技術採納曲線 3. 市場滲透過程 |
• 描述完整生長週期
• 有拐點 • 最終趨於穩定 |
| 逆函數 | $ y=a+\frac{b}{x} $ | 1. 引力與距離關係
2. 工作效率與干擾頻率 3. 服務響應時間與併發數 |
• 反比例關係
• 快速衰減後趨穩 • 適合漸近線模型 |
| 邏輯函數 | $ y=\frac{1}{\frac{1}{u}+ab^x} $ | 1. 人口增長(環境承載力)
2. 市場飽和分析 3. 疾病傳播(考慮免疫) |
• 完整的S型曲線
• 有明確上限u • 描述有限資源下的增長 |
4. 實戰演練:誰能預測“爆款視頻”的流量?
最後,我們來看一個熱點案例。
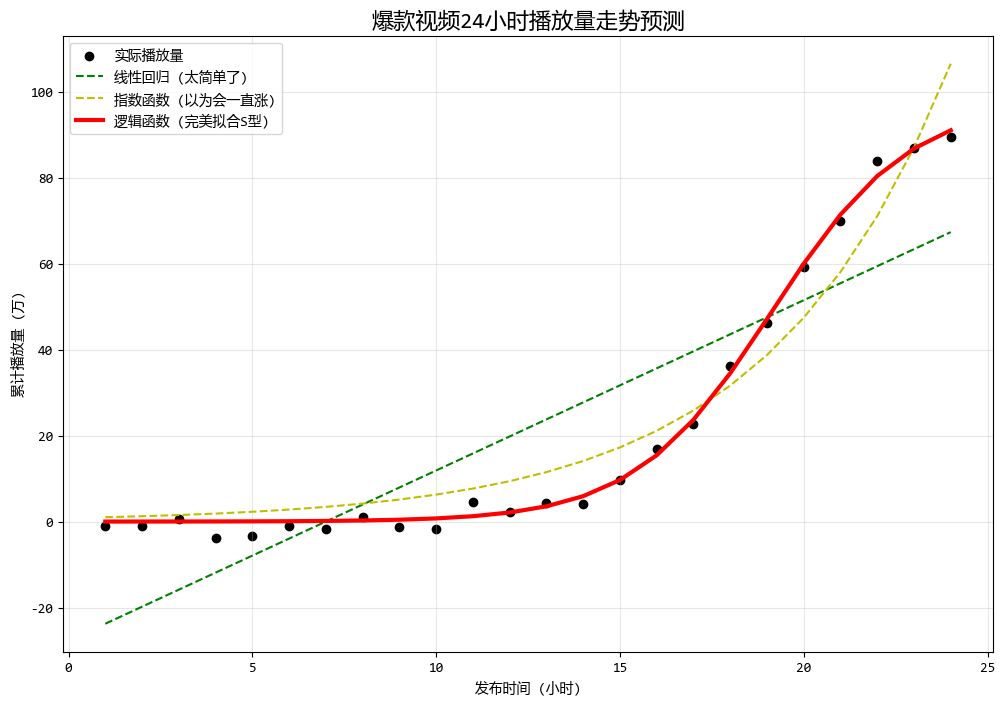
假設你是一個短視頻運營,你拿到了一款爆款視頻發佈後24小時內的累計播放量數據。
你需要判斷它的流量走勢,以便決定是否追加推廣預算。
視頻流量通常符合S型增長(邏輯函數):
- 冷啓動:沒人看。
- 爆發期:被算法推薦,指數級增長。
- 飽和期:該看的人都看過了,增長停滯。
如果不做分析,直接用線性迴歸(直線)去預測,後果可能是災難性的(會預測出無限增長)。
下面的代碼嘗試了線性迴歸和兩種不同的非線性迴歸函數來分析。
# --- 模擬爆款視頻數據 ---
x_data = np.linspace(1, 24, 24) # 24小時
# 真實數據模擬:符合邏輯函數分佈,上限是100萬播放量
y_data = 100 / (1 + 100 * np.exp(-0.5 * (x_data - 10))) + np.random.normal(0, 2, 24)
# y_data 單位是 萬次播放
plt.figure(figsize=(12, 8))
plt.scatter(x_data, y_data, label='實際播放量', color='black', marker='o')
# --- 挑戰1:嘗試用線性迴歸擬合 (錯誤的嘗試) ---
popt_lin, _ = curve_fit(lambda x, a, b: a*x+b, x_data, y_data)
y_lin = popt_lin[0] * x_data + popt_lin[1]
plt.plot(x_data, y_lin, 'g--', label='線性迴歸 (太簡單了)')
# --- 挑戰2:嘗試用指數函數擬合 (爆發期還可以,但無法預測飽和) ---
# 指數函數容易溢出,選取部分數據或小心參數初始值,這裏僅作演示
try:
popt_exp, _ = curve_fit(func_exponential, x_data, y_data, maxfev=5000)
y_exp = func_exponential(x_data, *popt_exp)
plt.plot(x_data, y_exp, 'y--', label='指數函數 (以為會一直漲)')
except:
print("指數擬合失敗,數據不符合指數特徵")
# --- 挑戰3:使用邏輯函數 (Logistic) 擬合 (最佳選擇) ---
# 邏輯函數公式較複雜,給一些初始猜測值(p0)會有幫助:上限u=100, a=100, b=0.5
# 注意:上面的func_logistic形式需要調整以匹配scipy擬合的穩定性,
# 這裏我們使用一個更通用的Logistic形式用於演示:L / (1 + exp(-k(x-x0)))
def standard_logistic(x, L, k, x0):
return L / (1 + np.exp(-k * (x - x0)))
popt_log, _ = curve_fit(standard_logistic, x_data, y_data, p0=[100, 0.5, 10])
y_log = standard_logistic(x_data, *popt_log)
plt.plot(x_data, y_log, 'r-', linewidth=3, label='邏輯函數 (完美擬合S型)')
# --- 繪圖美化 ---
plt.title('爆款視頻24小時播放量走勢預測', fontsize=16)
plt.xlabel('發佈時間 (小時)')
plt.ylabel('累計播放量 (萬)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
print(f"預測結論:該視頻的流量天花板大約在 {popt_log[0]:.1f} 萬次左右。")
# 運行結果:
'''
預測結論:該視頻的流量天花板大約在 97.7 萬次左右。
'''
從圖中可以看出:
- 綠線(線性):完全無法捕捉爆發的趨勢,早期預測偏高,中期預測偏低,晚期預測又偏低。
- 黃線(指數):在視頻爆發初期(前10小時)擬合得很好,但它會預測24小時後播放量破億,這顯然不符合實際(因為受眾是有限的)。
- 紅線(邏輯函數):完美地貼合了數據,不僅抓住了爆發期,還成功預測了流量的“天花板”(飽和點)。
5. 總結:如何選擇迴歸模型?
迴歸分析不僅是數據分析師工具箱中的基礎工具,更是連接數據與業務的橋樑。
作為一名數據分析師,選擇哪種迴歸模型,最終還是要根據數據和業務的情況來決定。
- 先看圖:拿到數據,先用
plt.scatter()畫散點圖。- 看着像直線? -> 線性迴歸。
- 看着像拋物線? -> 二次函數。
- 看着像先慢後快? -> 指數函數。
- 看着像S型? -> 邏輯函數。
- 看業務:
- 只要是涉及“資源有限”、“市場飽和”的,多半是 S曲線 或 對數函數。
- 只要是涉及“病毒傳播”、“裂變”的,初期多半是 指數函數。
- 看誤差:
- 用 $ R^2 $ 或 均方誤差(MSE)來評估,哪個模型誤差小,就選哪個。
迴歸分析並不難,難的是理解業務背後的邏輯,並選擇正確的數學模型去描述它。