在數據分析的江湖裏,我們經常會聽到老闆或業務方拋出這樣的問題:
- “現在的年輕人越晚睡,買護膚品是不是越瘋狂?”
- “我們APP的各種優惠券,真的能提升用户的留存率嗎?”
- “天氣越熱,這隻股票是不是跌得越慘?”
面對這些問題,很多新人容易犯 “憑感覺” 的錯誤:“我覺得應該有關係吧……”
數據分析不相信“我覺得”,只相信證據。 而尋找變量之間關係強弱的這個過程,就叫做相關分析。
今天,就帶大家把相關分析的工具箱翻個底朝天,從基礎到進階,一次性講透!
1. 什麼是相關分析?
簡單來説,相關分析就是判斷兩個或多個事物之間是否存在某種聯繫,以及這種聯繫有多緊密。
但請務必記住數據分析界的第一鐵律:相關 $ \neq $ 因果。
- 相關:公雞叫了,天亮了。(它倆有關係,經常一起發生)
- 因果:因為公雞叫了,所以天亮了。(這就錯了,天亮是因為地球自轉,不是因為雞叫)
我們要做的,就是用數值(相關係數)來量化這種“一起發生”的程度。
2. 數據相關的“三劍客”
皮爾森相關係數,斯皮爾曼相關係數和肯達爾相關係數,這是最常見的三種相關係數,它們處理的是數值型或者有等級順序的數據。
2.1. 皮爾森相關係數:精確測量的標準
皮爾森相關是最常用的相關性分析方法,適用於符合以下條件的數據:
- 連續數據(定距或定比尺度)
- 數據服從正態分佈
- 變量間呈線性關係
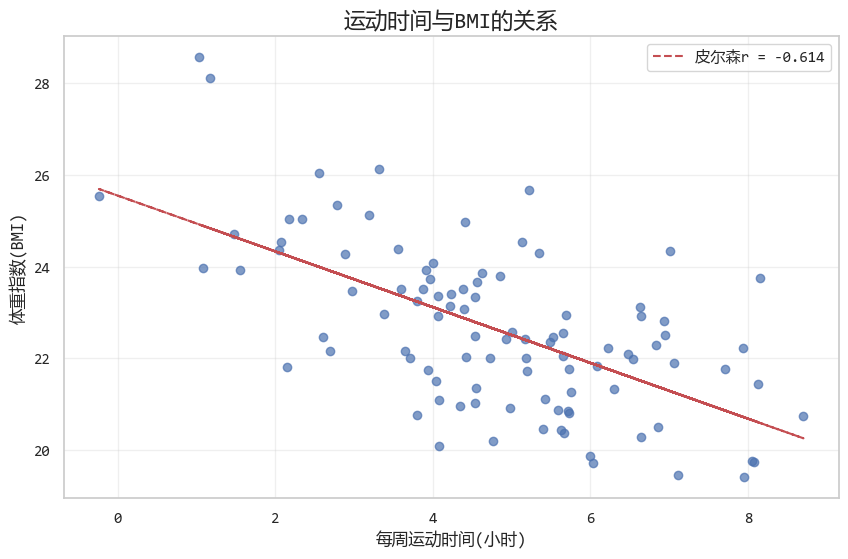
這是最“挑剔”也是最常用的指標。它要求數據是連續數值(定距/定比),並且最好服從正態分佈(鐘形曲線)。它衡量的是線性關係(是不是一條直線)。
比如:身高和體重。一般來説,人越高,體重越重,這是一個比較標準的線性關係。
它的取值範圍從 -1 到 1。接近 1 表示正相關(同漲同跌),接近 -1 表示負相關(此消彼長),0 表示沒關係。
代碼示例如下:
import numpy as np
import pandas as pd
from scipy import stats
# 模擬數據:運動時間(小時/周)與體重指數(BMI)
np.random.seed(42)
# 生成100個樣本
n_samples = 100
exercise_time = np.random.normal(5, 2, n_samples) # 平均每週運動5小時
# BMI與運動時間負相關(運動越多,BMI越低)
bmi = 25 - 0.5 * exercise_time + np.random.normal(0, 1.5, n_samples)
# 創建DataFrame
data = pd.DataFrame({'運動時間_小時每週': exercise_time, 'BMI': bmi})
# 計算皮爾森相關係數
pearson_corr, p_value = stats.pearsonr(data['運動時間_小時每週'], data['BMI'])
print(f"皮爾森相關係數: {pearson_corr:.3f}")
print(f"P值: {p_value:.5f}")
# 運行結果:
'''
皮爾森相關係數: -0.614
P值: 0.00000
'''
圖形展示的效果如下:
2.2. 斯皮爾曼相關係數:打破正態分佈的限制
如果數據不服從正態分佈,或者有極端值(比如馬雲的財富混進了我們的收入數據中),皮爾森相關係數就不準了。
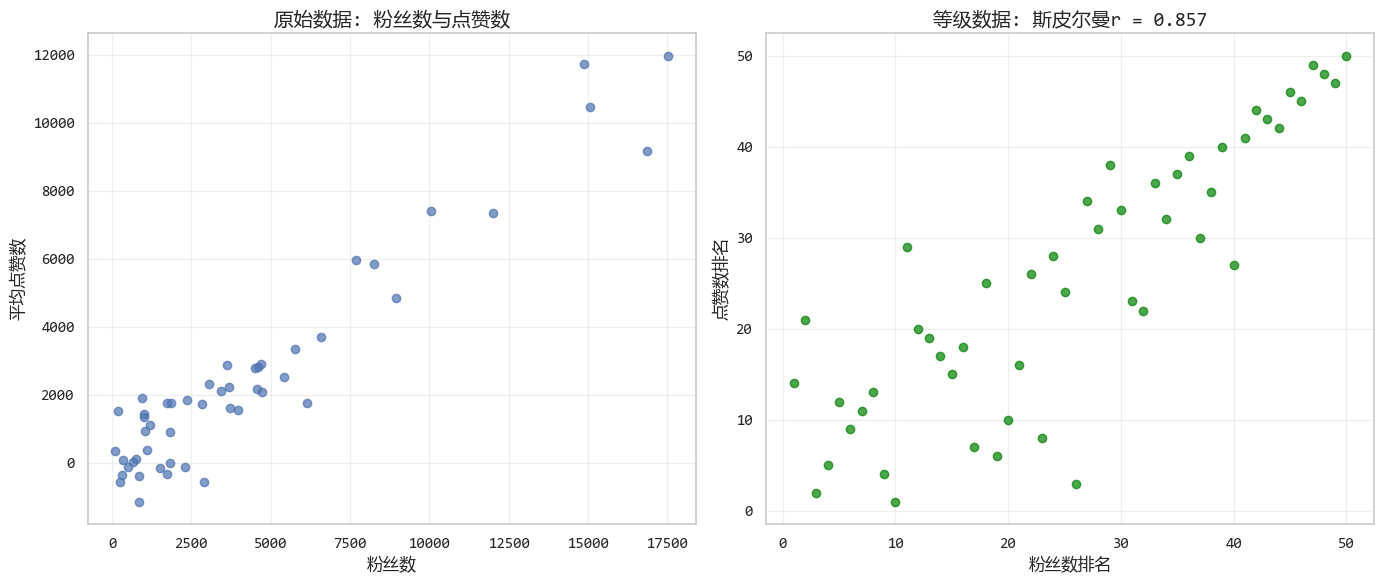
這時候用斯皮爾曼相關係數。它看重的是排名(Rank),而不是具體數值。
比如語文成績排名和數學成績排名,我們不關心具體考了多少分,只關心你的位次。
代碼示例如下:
# 模擬數據:社交媒體表現
np.random.seed(42)
# 生成非正態分佈的數據
followers = np.random.exponential(5000, 50) # 指數分佈
likes = 0.1 * followers**1.2 + np.random.normal(0, 1000, 50) # 非線性關係
# 創建DataFrame
social_data = pd.DataFrame({"粉絲數": followers, "平均點贊數": likes})
# 計算斯皮爾曼相關係數
spearman_corr, spearman_p = stats.spearmanr(
social_data["粉絲數"], social_data["平均點贊數"]
)
print(f"斯皮爾曼相關係數: {spearman_corr:.3f}")
print(f"P值: {spearman_p:.5f}")
# 運行結果:
'''
斯皮爾曼相關係數: 0.857
P值: 0.00000
'''
圖形化結果如下:
2.3. 肯達爾相關係數:小樣本和有序數據的首選
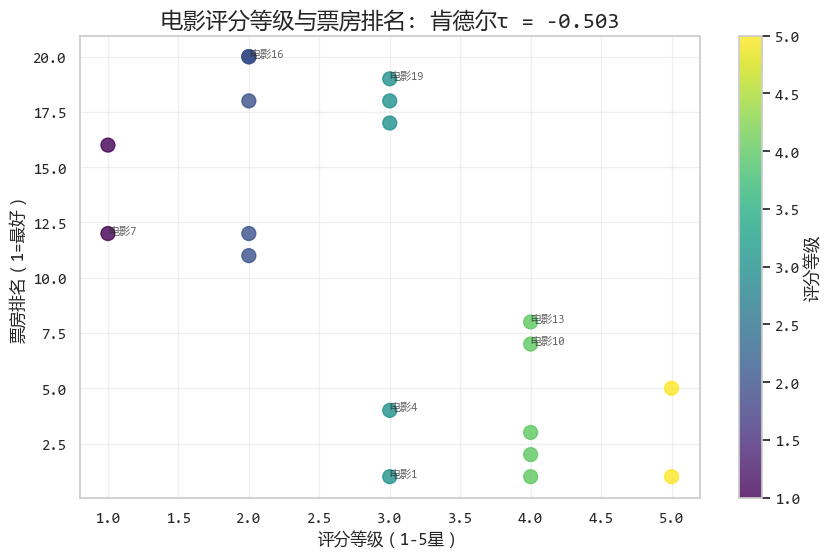
肯達爾相關也適用於等級數據,與斯皮爾曼相關不同,它更關注“和諧對”與“不和諧對”。
通常用於樣本量較小,或者數據有很多並列排名的情況。
比如:兩位面試官給5個候選人打分。我們要看這兩位面試官的審美標準是否一致。
代碼示例:
# 模擬數據:電影評分與票房
np.random.seed(42)
# 生成有序數據(電影評分和票房排名)
movie_data = pd.DataFrame(
{
"電影名稱": [f"電影{i}" for i in range(1, 21)],
"評分等級": np.random.choice(
[1, 2, 3, 4, 5], 20, p=[0.1, 0.2, 0.3, 0.3, 0.1]
), # 1-5星
"票房排名": np.arange(1, 21), # 票房排名
}
)
# 添加一些相關性:評分越高,票房排名越好(數字越小)
for i in range(len(movie_data)):
if movie_data.loc[i, "評分等級"] >= 4:
movie_data.loc[i, "票房排名"] = max(
1, movie_data.loc[i, "票房排名"] - np.random.randint(3, 8)
)
elif movie_data.loc[i, "評分等級"] <= 2:
movie_data.loc[i, "票房排名"] = min(
20, movie_data.loc[i, "票房排名"] + np.random.randint(3, 8)
)
# 計算肯德爾相關係數
kendall_corr, kendall_p = stats.kendalltau(
movie_data["評分等級"], movie_data["票房排名"]
)
print(f"肯德爾相關係數: {kendall_corr:.3f}")
print(f"P值: {kendall_p:.5f}")
# 運行結果:
'''
肯德爾相關係數: -0.503
P值: 0.00460
'''
圖形化結果如下:
3. 偏相關分析:誰是“第三者”?
有時候,兩個變量看起來關係很好,其實是因為有“第三者”在搗亂。
偏相關分析允許我們在控制其他變量的情況下,分析兩個變量之間的 "純" 相關性。
比如一個生活中的案例:“冰淇淋銷量” 和 “溺水事故數量”。
數據統計發現,冰淇淋賣得越好的日子,溺水的人越多(相關係數很高)。難道吃冰淇淋會導致溺水?
當然不是!背後的控制變量(第三者)是氣温。氣温高 -> 買冰淇淋多 & 游泳的人多 -> 溺水概率大。
想要正確分析,必須剔除控制變量(氣温)的影響後,再看另外兩個變量(冰淇淋和溺水)是否還相關。
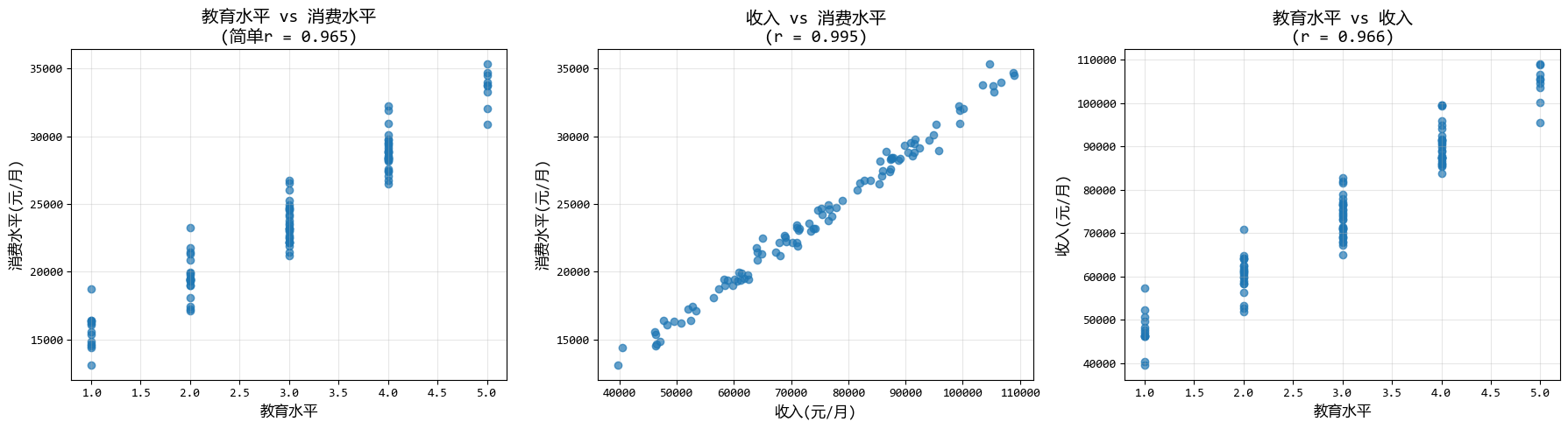
下面的示例中,我們先排除收入影響後,分析教育水平與消費水平的關係。
# 使用pingouin庫進行偏相關分析(需要安裝:pip install pingouin)
import pingouin as pg
# 模擬數據:教育水平、收入和消費水平
np.random.seed(42)
n = 100
# 教育水平(1-5,5為最高)
education = np.random.choice([1, 2, 3, 4, 5], n, p=[0.1, 0.2, 0.3, 0.3, 0.1])
# 收入與教育水平正相關
income = 30000 + 15000 * education + np.random.normal(0, 5000, n)
# 消費水平與收入和教育水平都相關
consumption = 1000 + 0.3 * income + 200 * education + np.random.normal(0, 500, n)
# 創建DataFrame
socioeconomic_data = pd.DataFrame(
{"教育水平": education, "收入_元每月": income, "消費水平": consumption}
)
print("=== 簡單相關分析 ===")
simple_corr, simple_p = stats.pearsonr(
socioeconomic_data["教育水平"], socioeconomic_data["消費水平"]
)
print(f"教育水平與消費水平的簡單相關係數: {simple_corr:.3f}")
print("\n=== 偏相關分析(控制收入)===")
# 使用pingouin進行偏相關分析
partial_corr = pg.partial_corr(
data=socioeconomic_data, x="教育水平", y="消費水平", covar="收入_元每月"
)
print(partial_corr.round(3))
# 運行結果:
'''
=== 簡單相關分析 ===
教育水平與消費水平的簡單相關係數: 0.965
=== 偏相關分析(控制收入)===
n r CI95% p-val
pearson 100 0.129 [-0.07, 0.32] 0.204
'''
圖形化結果如下:
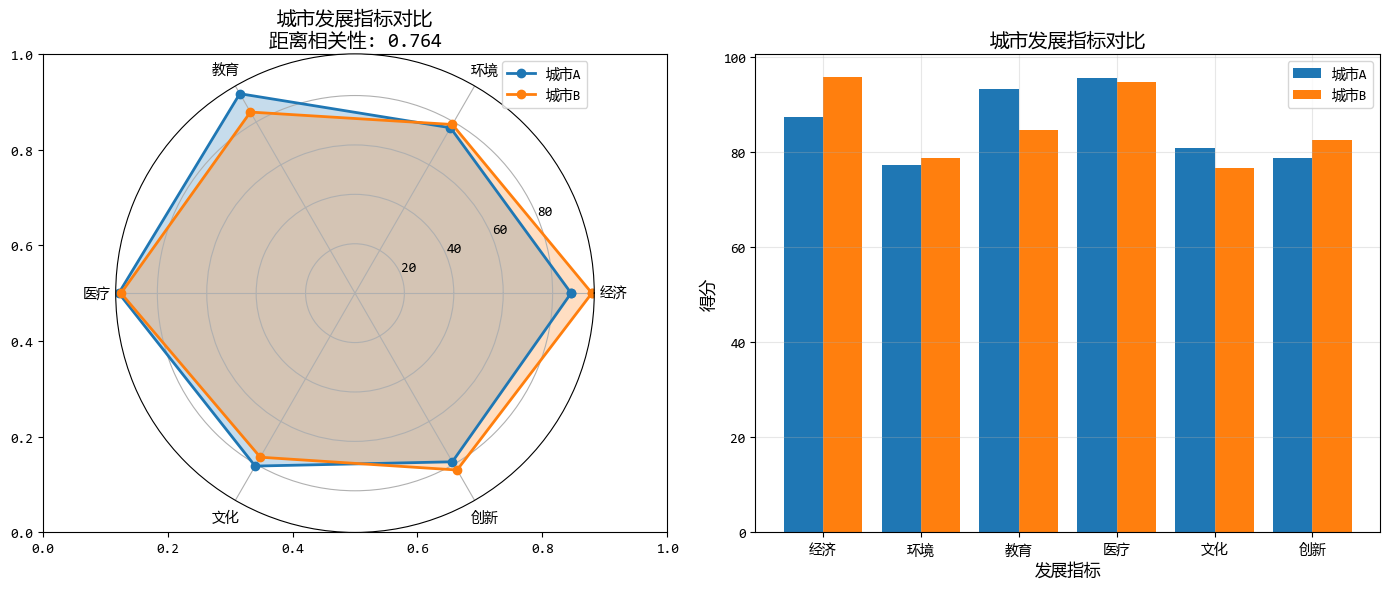
4. 距離相關分析:多變量關係的度量
距離相關分析可以衡量兩組變量(每個變量組包含多個指標)之間的相關性,是多變量分析的有力工具。
比如壓力與工作效率(耶克斯-多德森定律)的關係。
壓力太小,人會懶散(效率低);壓力太大,人會崩潰(效率低);只有適度的壓力,效率最高。
這是一個 U型(非線性) 關係。這時候用Pearson去算,結果可能是0(因為它找不到直線),但其實它們關係很緊密。
下面的示例,比較兩個城市的綜合發展水平(經濟、環境、社會等多維度指標)。
from scipy.spatial.distance import pdist, squareform
# 模擬數據:兩個城市的多維指標
np.random.seed(42)
# 城市A和城市B的6個發展指標(經濟、環境、教育、醫療、文化、創新)
indicators = ["經濟", "環境", "教育", "醫療", "文化", "創新"]
city_a = np.array([85, 78, 90, 88, 82, 80]) + np.random.normal(0, 5, 6)
city_b = np.array([88, 75, 87, 92, 79, 85]) + np.random.normal(0, 5, 6)
# 創建多個城市的比較數據
cities_data = pd.DataFrame(
{
"城市A": city_a,
"城市B": city_b,
"城市C": np.array([70, 85, 75, 80, 90, 72]) + np.random.normal(0, 5, 6),
"城市D": np.array([92, 70, 85, 87, 76, 91]) + np.random.normal(0, 5, 6),
"城市E": np.array([78, 88, 80, 85, 87, 78]) + np.random.normal(0, 5, 6),
},
index=indicators,
)
print("各城市發展指標數據:")
print(cities_data.round(2))
# 計算距離相關性(自定義簡化版)
def distance_correlation(x, y):
"""計算距離相關性"""
# 計算距離矩陣
def dist_matrix(v):
v = np.array(v)
n = len(v)
a = np.zeros((n, n))
for i in range(n):
for j in range(n):
a[i, j] = abs(v[i] - v[j])
return a
A = dist_matrix(x)
B = dist_matrix(y)
# 雙中心化
def double_centering(D):
n = len(D)
row_means = D.mean(axis=1)
col_means = D.mean(axis=0)
grand_mean = D.mean()
C = np.zeros((n, n))
for i in range(n):
for j in range(n):
C[i, j] = D[i, j] - row_means[i] - col_means[j] + grand_mean
return C
A_centered = double_centering(A)
B_centered = double_centering(B)
# 計算距離協方差和距離方差
dCov_XY = np.sqrt((A_centered * B_centered).sum() / (len(x) ** 2))
dVar_X = np.sqrt((A_centered * A_centered).sum() / (len(x) ** 2))
dVar_Y = np.sqrt((B_centered * B_centered).sum() / (len(x) ** 2))
# 計算距離相關性
dCor = dCov_XY / np.sqrt(dVar_X * dVar_Y)
return dCor
# 比較城市A和城市B的距離相關性
city_a_scores = cities_data["城市A"].values
city_b_scores = cities_data["城市B"].values
dcor = distance_correlation(city_a_scores, city_b_scores)
print(f"\n城市A與城市B的距離相關性: {dcor:.3f}")
# 運行結果:
'''
各城市發展指標數據:
城市A 城市B 城市C 城市D 城市E
經濟 87.48 95.90 71.21 87.46 75.28
環境 77.31 78.84 75.43 62.94 88.55
教育 93.24 84.65 66.38 92.33 74.25
醫療 95.62 94.71 77.19 85.87 86.88
文化 80.83 76.68 84.94 76.34 84.00
創新 78.83 82.67 73.57 83.88 76.54
城市A與城市B的距離相關性: 0.764
'''
圖形化的結果如下:
5. 相關性卡方檢驗:分類變量的關聯分析
如果我們分析的數據不是數字,而是類別(定類數據/低測度數據)呢?
當兩個變量都是分類變量(定類數據)時,我們可以使用卡方檢驗來分析它們之間是否存在關聯。
比如性別(男/女) 與 愛喝的飲料(奶茶/咖啡) 是否相關?
這裏沒有大小之分,只有類別。我們可以使用卡方檢驗來判斷兩個分類變量是否獨立。
下面的示例,我們嘗試分析性別與購物偏好類別之間的關係。
# 模擬數據:性別與購物偏好
np.random.seed(42)
# 創建列聯表
data = pd.DataFrame(
{
"性別": np.random.choice(["男", "女"], 200),
"購物偏好": np.random.choice(
["電子產品", "服裝鞋包", "美妝護膚", "運動户外", "家居生活"], 200
),
}
)
# 根據性別調整偏好概率(創建一些關聯)
for i in range(len(data)):
if data.loc[i, "性別"] == "男":
# 男性更可能偏好電子產品和運動户外
if np.random.random() < 0.3:
data.loc[i, "購物偏好"] = "電子產品"
elif np.random.random() < 0.5:
data.loc[i, "購物偏好"] = "運動户外"
else:
# 女性更可能偏好美妝護膚和服裝鞋包
if np.random.random() < 0.3:
data.loc[i, "購物偏好"] = "美妝護膚"
elif np.random.random() < 0.4:
data.loc[i, "購物偏好"] = "服裝鞋包"
# 創建列聯表
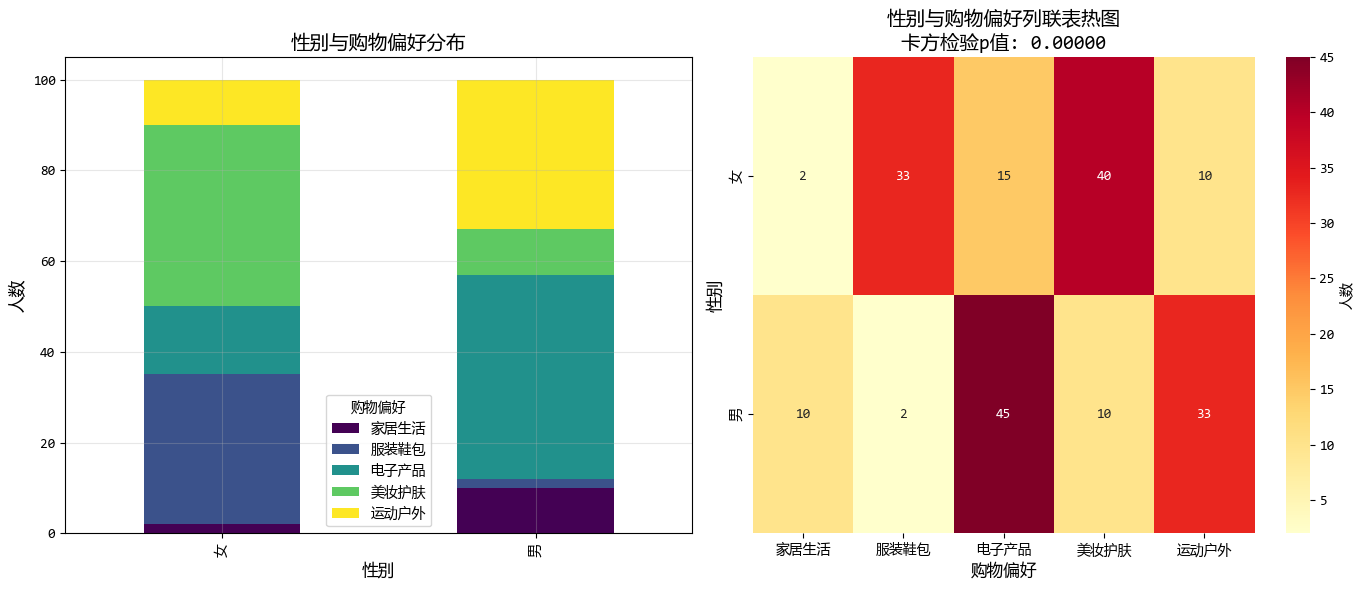
contingency_table = pd.crosstab(data["性別"], data["購物偏好"])
print("性別與購物偏好的列聯表:")
print(contingency_table)
# 執行卡方檢驗
chi2, p, dof, expected = stats.chi2_contingency(contingency_table)
print(f"\n卡方檢驗結果:")
print(f"卡方值: {chi2:.3f}")
print(f"P值: {p:.5f}")
print(f"自由度: {dof}")
print(f"\n期望頻數表:")
print(
pd.DataFrame(
expected, index=contingency_table.index, columns=contingency_table.columns
).round(2)
)
# 計算Cramer's V(衡量分類變量關聯強度)
def cramers_v(contingency_table):
"""計算Cramer's V係數"""
chi2 = stats.chi2_contingency(contingency_table)[0]
n = contingency_table.sum().sum()
min_dim = min(contingency_table.shape) - 1
v = np.sqrt(chi2 / (n * min_dim))
return v
cramers_v_value = cramers_v(contingency_table)
print(f"\nCramer's V係數: {cramers_v_value:.3f}")
print("解讀:0.1-0.3弱相關,0.3-0.5中等相關,>0.5強相關")
# 運行結果:
'''
性別與購物偏好的列聯表:
購物偏好 家居生活 服裝鞋包 電子產品 美妝護膚 運動户外
性別
女 2 33 15 40 10
男 10 2 45 10 33
卡方檢驗結果:
卡方值: 78.093
P值: 0.00000
自由度: 4
期望頻數表:
購物偏好 家居生活 服裝鞋包 電子產品 美妝護膚 運動户外
性別
女 6.0 17.5 30.0 25.0 21.5
男 6.0 17.5 30.0 25.0 21.5
Cramer's V係數: 0.625
解讀:0.1-0.3弱相關,0.3-0.5中等相關,>0.5強相關
'''
圖形化的結果如下:
6. 總結
數據分析師在面對變量關係時,要根據數據的 “長相” 來選工具:
| 方法 | 適用數據類型 | 特點 |
|---|---|---|
| 皮爾森相關 | 連續、正態分佈、線性關係 | 最常用,對異常值敏感 |
| 斯皮爾曼相關 | 連續但不正態,或有序數據 | 穩健,適用於單調關係 |
| 肯德爾相關 | 有序數據,小樣本 | 適合等級數據,解釋直觀 |
| 偏相關 | 需控制其他變量影響 | 揭示變量間的直接關係 |
| 距離相關 | 多變量組間關係 | 衡量多維度綜合關聯 |
| 卡方檢驗 | 分類變量 | 檢驗類別間關聯性 |
我們在分析數據相關性的時候,不要急於得出數據之間是否相關的結論。
先看看下面的注意事項是否有違背!
- 相關性不等於因果性:即使兩個變量高度相關,也不能斷定一個導致另一個
- 警惕第三變量問題:可能兩個變量都受到第三個未測量變量的影響
- 注意異常值的影響:異常值可能誇大或掩蓋真實的相關性
- 檢查線性假設:皮爾森相關要求線性關係,非線性關係需要其他方法
- 樣本大小的重要性:小樣本的相關性可能不穩定