數據分析時,我們經常需要從樣本數據推斷總體特徵。
而抽樣分佈就是連接樣本與總體的重要橋樑,如果你不理解它,就無法理解為什麼我們可以通過調查幾千人來預測全國的選舉結果,也無法理解A/B測試背後的邏輯。
本文將盡量使用大白話和Python代碼,帶你徹底搞懂抽樣分佈,並掌握最常用的四大分佈:Z分佈、T分佈、卡方分佈和F分佈。
1. 什麼是抽樣分佈
想象一下,你想了解全市高中生的平均身高,由於時間和資源限制,你不可能測量每個學生。
你的做法是:
去學校隨機挑選100位學生(這是一個樣本,Sample)。
計算這100位學生的平均身高,比如是150cm(這是統計量,Statistic)。
但是,一次抽樣可靠嗎?
如果你運氣不好,剛好選到的學生都是個子偏高的怎麼辦?
於是,你決定重複這個過程:
第2次,再選100位學生,算平均值是155cm。
第3次,再選100位學生,算平均值是148cm。
……
你重複了1000次。
現在,你手裏有了1000個“平均身高”的數據。如果你把這1000個數據畫成一個直方圖,這個圖展示的分佈,就是抽樣分佈。
一句話定義:
抽樣分佈不是原始數據的分佈,而是統計量(如平均值、方差)的概率分佈。
2. 抽樣分佈的重要性
在現實工作中,我們通常只有一次抽樣的機會(因為成本太高),我們手裏只有一個樣本數據。
我們面臨的終極問題是:
既然我看不到總體(所有中學生身高),我怎麼敢用手裏這唯一的樣本(100位學生的身高)去代表總體?
抽樣分佈 就是連接 “樣本” 和 “總體” 的橋樑:
總體是未知的真相,樣本是我們手裏的碎片。
抽樣分佈告訴我們:樣本統計量圍繞總體真值波動的規律。
知道了這個規律(分佈),我們就能算出:我手裏這個樣本,有多大的概率是靠譜的?
這就是置信區間和假設檢驗的基礎。
3. 四大常用抽樣分佈
接下來,我們介紹四種最常用的抽樣分佈,並使用Python代碼來做簡單的演示。
3.1. Z分佈
Z分佈是統計學中的“皇冠”。
當樣本量足夠大(通常n > 30)時,根據中心極限定理,樣本均值的分佈近似於正態分佈。
使用Z分佈的前提是,假設已知總體方差,或者樣本量極大以至於樣本方差可以代替總體方差。
它的使用場景一般在大樣本的均值檢驗(如:網站百萬流量下的轉化率分析)。
這種方法的優點在於其數學性質非常好,查表非常方便,而且計算過程也很簡單。
然而,它也存在一些侷限性,在現實生活中,我們很難準確地知道整個羣體的方差情況。
此外,在樣本數量較少的情況下,使用這種方法可能會導致較大的誤差。
下面用代碼模擬一個Z分佈的示例。
import numpy as np
import scipy.stats as stats
# 演示Z分佈在置信區間計算中的應用
# 假設我們調查了100名學生的月支出,平均值為2500元,已知總體標準差為500元
sample_mean = 2500 # 樣本平均值
population_std = 500 # 總體標準差
sample_size = 100 # 樣本數量
confidence_level = 0.95 # 置信水平
# 計算標準誤差
standard_error = population_std / np.sqrt(sample_size)
# 計算Z值 (95%置信水平對應的Z值)
z_value = stats.norm.ppf((1 + confidence_level) / 2)
# 計算置信區間
margin_of_error = z_value * standard_error
confidence_interval = (sample_mean - margin_of_error, sample_mean + margin_of_error)
print(f"樣本均值: {sample_mean}元")
print(f"95%置信區間: [{confidence_interval[0]:.2f}, {confidence_interval[1]:.2f}]元")
print(
f"這意味着我們有95%的把握認為總體平均月支出在{confidence_interval[0]:.2f}元到{confidence_interval[1]:.2f}元之間"
)
# 運行結果:
'''
樣本均值: 2500元
95%置信區間: [2402.00, 2598.00]元
這意味着我們有95%的把握認為總體平均月支出在2402.00元到2598.00元之間
'''
代碼中用到了scipy庫中的stats.norm.ppf()函數,這是累積分佈函數(CDF)的反函數,可用來計算Z值。
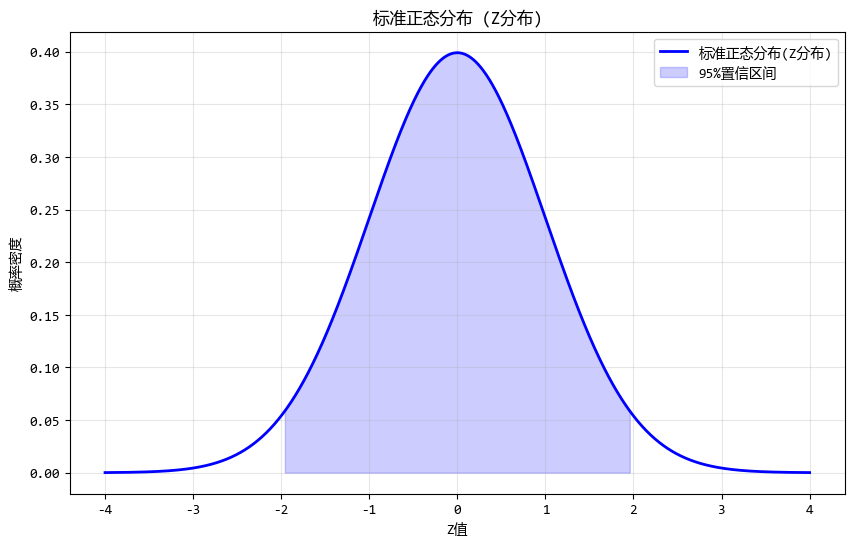
使用測試數據繪製的圖如下:
# 生成Z分佈數據
x = np.linspace(-4, 4, 1000)
z_distribution = stats.norm.pdf(x)
3.2. T分佈
T分佈是為了解決 “小樣本”問題而生的。
當你手頭數據很少(比如n < 30),且不知道總體方差時,Z分佈會低估誤差,這時候必須用T分佈。
比如,在小樣本實驗(比如只有10只小白鼠參與的藥物實驗)或AB測試的早期階段中,優先考慮使用T分佈。
當處理小規模的數據集時,T分佈能夠提供更加準確的結果。
這是因為T分佈具有所謂的“厚尾”特徵,這意味着它對於數據中的不確定性給予了更多的關注,特別是提高了對極端值出現可能性的認可。
這樣的特性使得在面對有限數量樣本的情況下,T分佈相較於Z分佈而言,能更真實地反映出數據的變異程度。
然而,T分佈並非沒有缺點。
隨着收集到的數據量不斷增加,我們會觀察到T分佈逐漸趨向於標準正態分佈,也就是我們常説的Z分佈。
這表明,在大規模數據集面前,T分佈所提供的額外靈活性變得不那麼顯著了。
下面用代碼模擬一個T分佈的示例。
# T分佈在置信區間計算中的應用
# 假設我們調查了25名員工的月薪,平均值為8000元,樣本標準差為1500元
sample_mean = 8000 # 樣本平均值
sample_std = 1500 # 樣本標準差
sample_size = 25 # 樣本數量
confidence_level = 0.95 # 置信水平
# 計算標準誤
standard_error = sample_std / np.sqrt(sample_size)
# 計算T值 (95%置信水平,自由度=n-1)
t_value = stats.t.ppf((1 + confidence_level) / 2, sample_size - 1)
# 計算置信區間
margin_of_error = t_value * standard_error
confidence_interval = (sample_mean - margin_of_error, sample_mean + margin_of_error)
print(f"樣本均值: {sample_mean}元")
print(f"樣本標準差: {sample_std}元")
print(f"樣本大小: {sample_size}")
print(f"95%置信區間: [{confidence_interval[0]:.2f}, {confidence_interval[1]:.2f}]元")
print(f"注意:由於樣本量較小且總體方差未知,我們使用T分佈而不是Z分佈")
# 運行結果:
'''
樣本均值: 8000元
樣本標準差: 1500元
樣本大小: 25
95%置信區間: [7380.83, 8619.17]元
注意:由於樣本量較小且總體方差未知,我們使用T分佈而不是Z分佈
'''
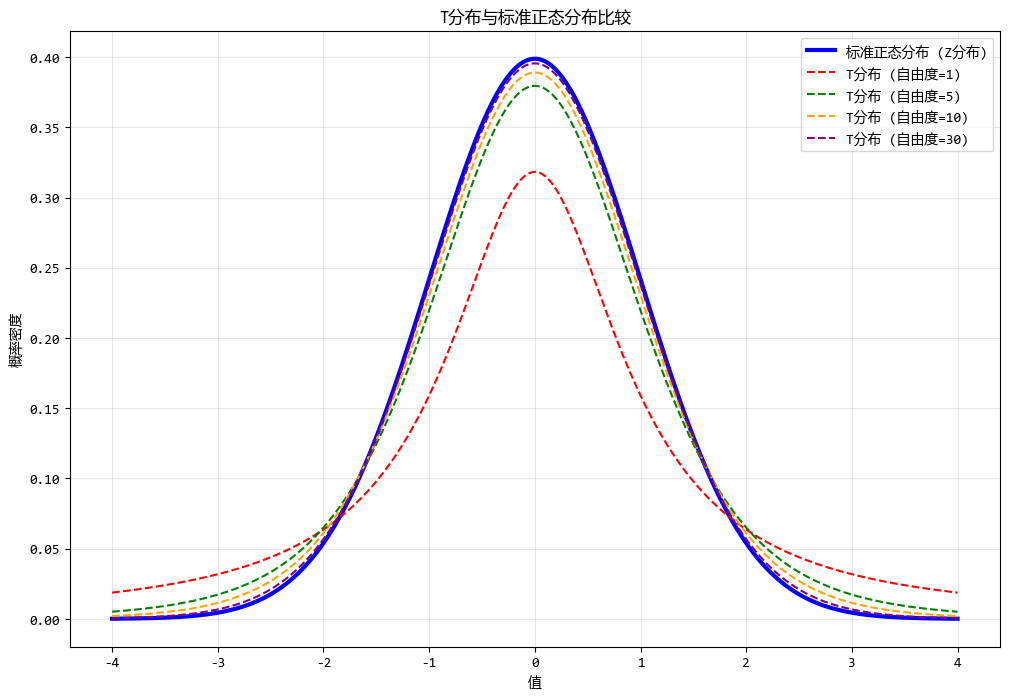
使用測試數據繪製不同自由度的T分佈圖形如下:
# 生成數據
x = np.linspace(-4, 4, 1000)
z_distribution = stats.norm.pdf(x)
# 繪製不同自由度的T分佈
degrees_of_freedom = [1, 5, 10, 30]
for df in degrees_of_freedom:
t_distribution = stats.t.pdf(x, df)
3.3. 卡方分佈
前兩個分佈主要用於處理 “數值型” 數據(平均值),而 卡方分佈 主要用於 “類別型” 數據。
卡方分佈的主要應用場景有:
- 獨立性檢驗:性別和購買偏好是否有關係?
- 擬合優度檢驗:這枚骰子是否均勻(實際觀測頻數 vs 理論期望頻數)?
- 方差的檢驗:生產零件的波動率是否在控制範圍內?
卡方分佈在處理非數值型數據,比如分類數據時特別有用。
不過,它也有一定的侷限性,首先,它對樣本數量有一定的要求,通常每個類別中的樣本數不能太少,否則結果可能不太準確。
另外,這種方法得到的結果分佈是不對稱的,並且只會出現正值。
下面用代碼模擬一個卡方分佈的示例。
# 卡方分佈在獨立性檢驗中的應用示例
# 模擬一個問卷調查數據:性別與產品偏好是否獨立
# 創建模擬數據
observed = np.array(
[[30, 20, 10], [15, 25, 20]] # 男性選擇A、B、C產品的人數
) # 女性選擇A、B、C產品的人數
print("觀察到的列聯表:")
print(" 產品A 產品B 產品C")
print(f"男性 {observed[0][0]} {observed[0][1]} {observed[0][2]}")
print(f"女性 {observed[1][0]} {observed[1][1]} {observed[1][2]}")
# 執行卡方獨立性檢驗
chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)
print(f"\n卡方檢驗結果:")
print(f"卡方統計量: {chi2_stat:.4f}")
print(f"P值: {p_value:.4f}")
print(f"自由度: {dof}")
alpha = 0.05
if p_value < alpha:
print("結論: 拒絕原假設,性別與產品偏好之間存在顯著關聯")
else:
print("結論: 無法拒絕原假設,性別與產品偏好之間沒有顯著關聯")
# 運行結果:
'''
觀察到的列聯表:
產品A 產品B 產品C
男性 30 20 10
女性 15 25 20
卡方檢驗結果:
卡方統計量: 8.8889
P值: 0.0117
自由度: 2
結論: 拒絕原假設,性別與產品偏好之間存在顯著關聯
'''
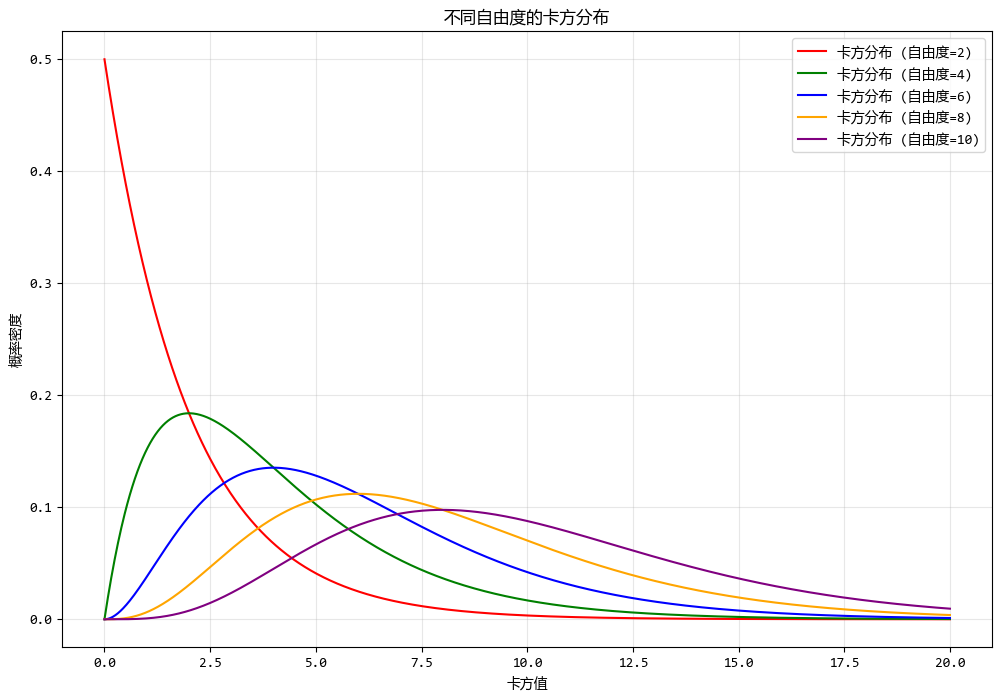
使用測試數據繪製不同自由度的卡方分佈圖形如下:
x = np.linspace(0, 20, 1000)
degrees_of_freedom_chi2 = [2, 4, 6, 8, 10]
for df in degrees_of_freedom_chi2:
chi2_distribution = stats.chi2.pdf(x, df)
3.4. F分佈
F分佈主要關注兩個方差的比率。如果説T檢驗是比 “均值” ,那F檢驗就是比 “波動” 。
F分佈的主要應用場景有:
- 方差分析 (
ANOVA):比較3組及以上數據的均值差異(本質是比較組間方差和組內方差的比值)。 - 比較兩個總體方差:機器A和機器B生產的產品,誰的質量更穩定?
F分佈是ANOVA分析的核心,它的優勢在於它能夠同時處理多組數據之間的差異。
然而,其侷限性表現在對數據正態性假設的敏感度較高。
下面用代碼模擬一個F分佈的示例。
# F分佈在方差分析中的應用示例
# 模擬三種不同教學方法下學生的考試成績
np.random.seed(42) # 確保結果可重現
# 生成三個組的模擬成績數據
method_a = np.random.normal(75, 8, 30) # 教學方法A
method_b = np.random.normal(80, 10, 30) # 教學方法B
method_c = np.random.normal(72, 9, 30) # 教學方法C
# 執行單因素方差分析
f_stat, p_value = stats.f_oneway(method_a, method_b, method_c)
print("方差分析(ANOVA)示例: 比較三種教學方法的效果")
print(
f"教學方法A: 平均分 = {np.mean(method_a):.2f}, 標準差 = {np.std(method_a, ddof=1):.2f}"
)
print(
f"教學方法B: 平均分 = {np.mean(method_b):.2f}, 標準差 = {np.std(method_b, ddof=1):.2f}"
)
print(
f"教學方法C: 平均分 = {np.mean(method_c):.2f}, 標準差 = {np.std(method_c, ddof=1):.2f}"
)
print(f"\n方差分析結果:")
print(f"F統計量: {f_stat:.4f}")
print(f"P值: {p_value:.4f}")
alpha = 0.05
if p_value < alpha:
print("結論: 拒絕原假設,至少有一種教學方法的效果與其他方法有顯著差異")
else:
print("結論: 無法拒絕原假設,三種教學方法的效果沒有顯著差異")
# 運行結果:
'''
方差分析(ANOVA)示例: 比較三種教學方法的效果
教學方法A: 平均分 = 73.49, 標準差 = 7.20
教學方法B: 平均分 = 78.79, 標準差 = 9.31
教學方法C: 平均分 = 72.12, 標準差 = 8.93
方差分析結果:
F統計量: 5.1166
P值: 0.0079
結論: 拒絕原假設,至少有一種教學方法的效果與其他方法有顯著差異
'''
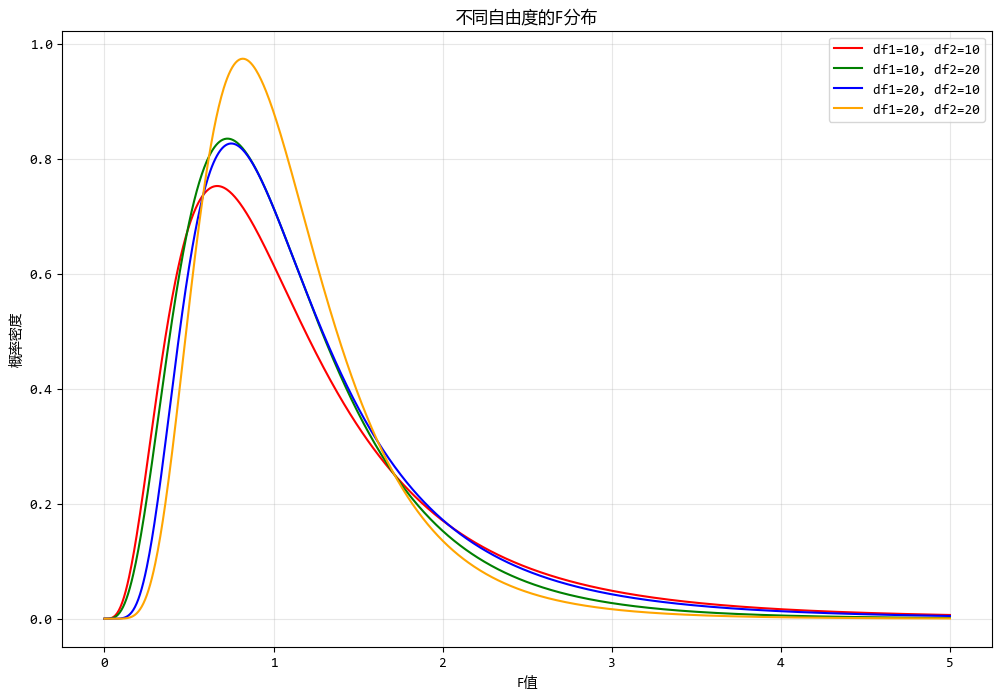
使用測試數據繪製不同自由度的F分佈圖形如下:
x = np.linspace(0, 5, 1000)
# 定義幾組自由度組合
df_combinations = [(10, 10), (10, 20), (20, 10), (20, 20)]
for (df1, df2) in df_combinations:
f_distribution = stats.f.pdf(x, df1, df2)
4. 總結
最後,為了理清思路,我整理了一個對比表格。
當我們面對數據時,可以按圖索驥:
| 分佈名稱 | 核心關鍵詞 | 典型應用場景 | 數據類型 |
|---|---|---|---|
| Z分佈 | 大樣本、標準 | 樣本量>30,已知總體方差的均值檢驗 | 數值型 (Continuous) |
| T分佈 | 小樣本、修正 | 樣本量<30,未知總體方差,AB測試 | 數值型 (Continuous) |
| 卡方分佈 | 分類、獨立性 | 檢驗男女是否偏好不同,骰子是否均勻 | 類別型 (Categorical) / 方差 |
| F分佈 | 多組比較、方差比 | ANOVA方差分析(3組以上均值對比) | 數值型 (比率) |
數據分析不僅僅是敲代碼(Python)或畫圖(Tableau/Excel),其靈魂在於統計思維。
抽樣分佈告訴我們要對隨機性保持敬畏:不要輕信一次結果,要看這次結果在分佈中的位置。